Часть 3. Комбинаторика

Комбинаторика – это раздел дискретной математики, в котором рассматриваются возможности расположения, упорядочения, или выбора элементов некоторого конечного множества.

При решении многих практических задач приходится выбирать из некоторой совокупности объектов элементы, обладающие тем или иным свойством, подсчитывать, сколько различных комбинаций можно составить из конечного числа элементов, принадлежащих заданной совокупности, располагать эти элементы в определённом порядке и т.д. Поскольку в таких задачах речь идёт о тех или иных комбинациях объектов, то их называют комбинаторными задачами, а область математики, в которой они изучаются, - комбинаторикой.

Существует 2 основных закона, с помощью которых решаются многие задачи комбинаторики – правило суммы и правило произведения.

§1. Правило суммы.

Рассмотрим пример.

Если на одной полке шкафа стоит 30 книг, а на другой – 40 различных книг, и среди нет таких , которые есть на первой полке, то выбрать одну книгу из стоящих на этих полках можно 30+40=70 способами.

Обобщением этого примера является правило суммы, которое на языке теории множеств формулируется так:

Если пересечение конечных множеств А и В пусто, то число элементов в их объединении равно сумме мощностей множеств А и В. Если АВ=, то А  В= А+В.

Пояснение. Если элемент аА можно выбрать m способами, а элемент bB – способами, то выбор элемента хАВ можно осуществить m+n способами.

Пример. На ж/д вокзал ведут 2 автобусных маршрута, 4 троллейбусных маршрута и 3 маршрута такси. Сколько имеется способов доехать до ж/д вокзала на общественном транспорте без пересадок?

Следствие. Если конечные множества А1,А2,…,Ак попарно не пересекаются то имеет место равенство:А1А2…Ак=А1+А2+…+Ак.

§2.Правило произведения.

Рассмотрим пример. Имеется 2 светофора: первый с 3-мя лампами , может давать 3 сигнала - (К, Ж, З), второй с 2-мя лампами, может давать 2 сигнала(К, З). Сколько всего сигналов может быть получено при одновременной работе этих светофоров.

Решение. Существует 3 возможности получения сигнала 1-го светофора. При каждом сигнале 1-го светофора еще двумя способами может быть получен сигнал 2-го светофора. Способов, которыми можно получить сигнал при одновременной работе светофоров - 32=6. Графическая иллюстрация:

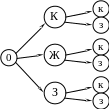
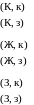
Это дерево. Исходную точку обозначим 0. Двигаясь всевозможными путями из 0 к правым крайним вершинам, мы получим 6 сигналов, которые можно получить в данной ситуации.

Обобщением этого примера является правило произведения:

Пусть А и В – конечные множества, А=m и В=n .Тогда А×В=mn.

Пояснение. Если элемент аА можно выбрать m способами, и если после каждого такого выбора элемент bB можно выбрать n способами, то выбор пары (a, b)A*B в указанном порядке можно осуществить А×В=m  n способами.

Задача. Найти число маршрутов из пункта М в пункт N через пункт К, если из М в К ведут 5 дорог, а из к в N – 3 дороги.

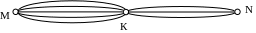
Решение. Введём 2 множества S={s1, s2, s3, s4, s5} – дорога из М в К, T={t1, t2, t3} – дорога из К в N. Теперь дорогу из М в N можно представить парой ( si, tj ), где i=1, 2, 3, 4, 5; j=1, 2, 3. Значит, ST – это множество всех дорог из М в N, количество которых равно S×T=53=15.

Следствие. Пусть Х1, Х2, Х3, …, Хк – произвольные множества, Хi=ni, . ТогдаХ1×Х2×…×Хк=(х1, х2, …, хк)хiХi, = n1…nk.