§3. Комбинаторные объекты.

При выборе k элементов из n различных элементов говорят, что они образуют выборки (расстановки, комбинации) из n элементов по k, или k-выборки.

В зависимости от того, имеет ли значение порядок элементов в комбинации, а также от того, входят ли в комбинацию все n элементов или только часть их, различают 3 вида комбинаций: размещения, перестановки и сочетания.

Размещение и сочетание может быть с повторением элементов и без повторений.

Ч исло всех размещений длины k из n элементов с повторениями:

Число всех размещений длины k

из n элементов без повторений:

Число всех перестановок на множестве из n элементов: An = n!

Ч исло всех сочетаний из n элементов по k (без повторений):

Порядок элементов

не учитывается

Порядок элементов

не учитывается

Порядок элементов

учитывается

Число всех сочетаний из n элементов по k (с повторениями):

1. Размещения с повторениями.

Формулировка задачи. Имеются предметы n различных видов а1,а2,а3,…,аn. Из них составляются всевозможные расстановки длины k. Т.е. дано множество, и любой его элемент можно брать в расстановку сколь угодно раз, но не более k.

а1,a2,a3,a4,a5,a6 Расстановка длины 7: а1 a2 a3 a3 a4 a2 a1.

Такие расстановки называются размещениями с повторениями из n по k(элементы одного вида могут повторяться).

Найдём число всевозможных расстановок, среди которых 2 расстановки считаются различными, если они отличаются или видом входящих в них предметов, или порядком этих предметов.

При составлении расстановки длины k имеется k мест, на каждое можно поставить предмет вида из имеющихся n видов а1,а2,а3,…,аn.

n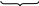 n n …n - количество всевозможных размещений с повторениями из n

k предметов по k.

Или, в терминах теории множеств:

Рассмотрим множества Х1,Х2,…,Хk такие, что Х1=Х2=…=Хk=а1,а2,а3,…,аn. Тогда все размещения с повторениями составляют множество Х1× Х2 ×…×Хk. По правилу прямого произведения получаем, что общее число размещений с повторениями из n по k равно: Х1× Х2 ×…×Хk  =nk.

Задача. Сколькими способами можно раскрасить квадрат, разделённый на 4 части, пятью цветами, допуская окрашивание разных частей в один цвет?

Задача. Найти количество всех пятизначных чисел.

Решение. Введём 5 множеств A₂=A₃=A₄=A₅=0,1,…,9, A₁=1,2,…,9.

Тогда все пятизначные числа составят прямое произведение указанных множеств

A₁×A₂×A₃×A₄×A₅=910101010=900000.

2. Размещение без повторений.

Имеется n различных символов а₁,а₂,а₃,…,а_n. Сколько из них можно составить расстановок длины k. Каждый элемент можно взять в расстановку только один раз. Две расстановки считаются различными, если они отличаются входящими в них элементами или порядком их в расстановке. Такие расстановки называются размещениями без повторений.

При составлении данных расстановок на 1-е место можно поставить любой из имеющихся n предметов, на 2-е – любой из n-1 оставшихся,…, на k-е место – любой из n-(k-1)=n-k+1 оставшихся.

n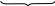 n-1 … n-k+1

k

По правилу прямого произведения получаем, что общее число размещений без повторений из n по k равно .

Задача. В хоккейном турнире участвуют 17 команд. Разыгрываются золотая, серебренная и бронзовая медали. Сколькими способами могут быть распределены медали?

Решение.17 команд претендуют на 3 места. Тогда тройку призёров можно выбрать способами

.

3. Перестановки (без повторений).

При составлении размещений без повторений из n по k мы получаем расстановки, отличающиеся друг от друга либо составом, либо порядком элементов.

Расстановки включающие все n элементов, могут отличаться друг от друга только порядком входящих в них элементов.

Такие расстановки называются перестановками из n элементов.

n n-1 …1 Число всевозможных перестановок из n элементов:

n

Задача. Сколько всего шестизначных чётных чисел можно составить из цифр 1,3,4,5,7 и 9, если из этих цифр ни одна не повторяется?

Решение. Что бы число было чётным, его последней цифрой должна быть из имеющихся только цифра 4. Остальные 5 цифр на оставшихся местах могут стоять в любом порядке. Следовательно, поставленная задача сводится к нахождению числа перестановок из 5 элементов. А₅=5!=120-всего чисел.

4. Перестановки с повторениями.

До сих пор мы считали, что все предметы в перестановке попарно различны. Если же некоторые переставляемое одинаковы, то получится меньше перестановок- некоторые перестановки совпадают друг с другом.

Формулировка задачи. Имеются предметы k различных видов. Сколько перестановок можно сделать из r₁ элементов 1-го вида, r₂ элементов 2-го вида, …, r_k элементов k-го вида.

Решение. Число элементов в каждой перестановке равно r₁+r₂+…+r_k=n. Если бы все предметы были различны, то число всех перестановок равнялось бы n! Но из-за того, что некоторые предметы совпадают, получится меньшее число перестановок.

Н апример, возьмём перестановку aa…a bb…b … xx…x, в которой сначала выписаны все элементы

r₁ r₂ r_k

1-го вида, затем все элементы 2-го вида, …, и все элементы k-го вида. Элементы 1-го вида можно переставить между собой r₁! способами, но т.к. все переставляемые элементы одинаковы, то такие перестановки ничего не меняют. Так же ничего не меняет r₂! перестановка элементов 2-го вида, …, r_k! перестановок k вида.

Перестановки элементов 1-го, 2-го, и т.д. видов можно делать независимо друг от друга. Поэтому по правилу произведения элементы перестановки можно переставлять друг с другом r₁!r₂!…r_k! способами так, что она остаётся неизменной. То же самое верно и для любого другого расположения элементов.

Поэтому число различных перестановок с повторениями, которые можно сделать из n элементов, равно:

, гдеr₁+r₂+…+r_k=n.

Задача. Всевозможные перестановки из букв слова «март» существует 4!=24. Перестановок из букв слова «мама»

Сколькими способами можно расположить в ряд 2 зелёные и 4 красные лампочки?

Р(2,4)= .

5. Сочетания (без повторений).

В тех случаях, когда нас не интересует порядок элементов в расстановке, а интересует лишь её состав, то говорят о сочетании.

Сочетаниями из n различных элементов по k называют всевозможные расстановки длины k, образованные из этих элементов и отличающиеся друг от друга составом, но не порядком элементов.

Общее число сочетаний обозначают или

Определяем, чему равно это число. Составим все сочетания из n по k, то есть выберем k предметов из n разных предметов всеми способами.

Затем переставим в каждом сочетании элементы всеми возможными способами. Таким образом, получим расстановки, отличающиеся либо порядком, либо составом, то есть это все размещения без повторений из n по k. Их число равно .

Учитывая, что каждое сочетание k! Размещений, по правилу произведения можно записать:

. Отсюда

Задача. Из состава конференций, на которой присутствует 52 человека, надо избрать делегацию, состоящую из 5 человек. Сколькими способами это можно сделать?

Решение.

6. Сочетание с повторениями.

Формулировка задачи. Имеются n видов элементов. Сколько  из них расстановок длины r, если не принимать во внимание порядок элементов?

Выведем формулу.

x₁,x₂,…,x_n- n элементов.

Рассмотрим произвольные сочетания с повторениями длины r например из элементов x₁,x₂,x₃,x_n.

x ₁x₂x₃x₃x_nx₁x₁…x₁x₂x_n.

r

Так как порядок элементов в сочетаниях не учитывается, то это сочетание можно записать так:

x₁x₁...x₁x₂x₂…x₂…..x_nx_n…x_n.

То есть мы рассматриваем места n для r элементов, и для разделителей между ними. Причем разделителей, независимо от количества элементов, из которых составлено сочетание, всегда должно быть n-1. Если элементы какого-то вида в сочетании отсутствуют, то разделители присутствуют всё равно.

x₁x₂…x_n-1x_n.

x₁…x_1.