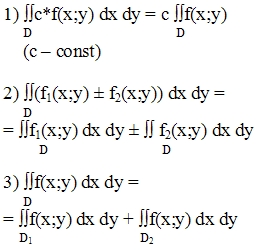8. Несобственные интегралы от неограниченных функций.

Пусть функция f(x)  интегрируема на любом отрезке, целиком содержащемся в промежутке [a;b), и бесконечно большая в точке x=b. Если существует предел  , то этот предел называют несобственным интегралом от неограниченной функции f(x)по (a, b) и обозначают его  . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле  . Аналогично определен интеграл  от интегрируемой на любом конечном отрезке, содержащемся в (a;b], бесконечно большой в точке  x=a функции f(x). Если пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.

9.Функции нескольких переменных, прел и непрерывность.

Пусть функция Z=f(M) определена на некотором множестве {M} и точка M₀ {M} или M₀ {M}, но обладает тем свойством, что в любой δ-окрестности этой точки содержится хотя бы одна точка множества {M}, отличная от M₀.

Предел: Число А называется пределом функции Z=f(M) в точке M₀, если функция Z=f(M) определена в окрестности точки M₀ и для любого ε>0, δ>0 такое что при |M₀M|<δ, выполняется неравенство |f(M)-A|<ε.

обозначение: 

Непрерывность: Функция Z=f(M) называется непрерывной в точке M₀, если предел функции в этой точке существует и равен значению функции в этой точке, т.е.

10.Частная производная:

В математическом анализе, частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.

В явном виде частная производная функции f определяется следующим образом:

Частным дифференциалом по х функции Z=f(x, y) называется главная часть частного приращения Δ_xZ=f(x+Δx,y)-f(x,y), пропорциональная приращению Δx независимой переменной х. Аналогично определяется частный дифференциал по у, т.е. Δ_yZ=f(y+Δy,x)-f(x,y).

Дифференциалы независимых переменных х и у просто равны их приращениям, т.е. dx=Δx, dy=Δy. Частные дифференциалы обозначаются так: d_xZ -частный дифференциал по х, d_yZ - частный дифференциал по у. При этом:

Таким образом, частный дифференциал функции двух независимых переменных равен произведению соответствующей частной производной на дифференциал этой переменной.

 Полным дифференциалом функции двух переменных называется главная часть полного приращения функции, линейная относительно приращений независимых переменных.

Теорема. Полный дифференциал функции двух независимых переменных равен сумме произведений частных производных функции на дифференциалы соответствующих независимых переменных.

dZ=f'_x(x,y)dx+f'_y(x,y)dy или 

Так как  dx=d_xZ и  dy=d_yZ, то dZ=d_xZ+d_yZ, т.е. дифференциал функции двух независимых переменных равен сумме ее частных дифференциалов.

11. Правило дифференцирования сложной функции позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x₀, а функция g имеет производную в точке y₀=f(x₀), то сложная функция h(x) = g(f(x)) также имеет производную в точке x₀.

Одномерный случай: Пусть даны функции, определённые в окрестностях на числовой прямой, f:u(x₀)→v(y₀)  где y₀=f(x₀) и  g:v(y₀)→R.  Пусть также эти функции дифференцируемы:   Тогда их композиция также дифференцируема:   и её производная имеет вид:

Замечание:В обозначениях Лейбница цепное правило для вычисления производной функции y=y(x) где x=x(t) принимает следующий вид:

Многомерный случай:Пусть даны функции   где y₀=f(x₀) и   Пусть также эти функции дифференцируемы:   и   Тогда их композиция тоже дифференцируема, и её дифференциал имеет вид

Полная производная функции — производная функции по времени вдоль траектории.

Расчёт полной производной функции   по времени t,    не подразумевает, что другие аргументы постоянны при изменяющемся t. Полная производная включает в себя эти непрямые зависимости от t (т.е. x(t)и y(t)) для описания зависимости f от t.

12. Частные производные высших порядков

Пусть задана функция f(x, y). Тогда каждая из ее частных производных  и  , которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная   обозначается через   или  , а   через   или  . Таким образом,

, 

Производные   и   называются частными производными второго порядка.  Частной производной второго порядка от функции z=f(x;y) дифференцируемой в области D, называется первая производная от соответствующей частной производной. Рассматривая частные производные от них, получим всевозможные частные производные третьего порядка:  ,  ,   и т. д.

 Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности.

13.Производная неявно заданной функции. Во многих задачах функция  y(x) задана невным образом. Например, для приведенных ниже функций

невозможно получить зависимость y(x) в явном виде.  Алгоритм вычисления производной  y'(x) от неявной функции выглядит следующим образом:Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая,  что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции;Решить полученное уравнение относительно производной  y'(x).

14.Экстрэмумы функций двух переменных. Функция z=f(x,y) имеет максимум в точке M₀(x₀;y₀), т.е. при  x=x₀, y=y₀ , если  f(x₀,y₀)>f(x,y) для всех точек (x,y), достаточно близких к точке (x₀,y₀) и отличных от неё.

Функция z=f(x,y) имеет минимум в точке M₀(x₀;y₀) , т.е. при  x=x₀, y=y_0,  если   f(x₀,y₀)<f(x,y)для всех точек (x,y), достаточно близких к точке (x₀,y₀)  и отличных от неё.

Максимум и минимум функции называются экстремумами функции.

Необходимые условия экстремума. Если точка x_о является точкой экстремума функции f(x), то либо f ^'(x_о) = 0, либо f (x_о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о - критическая точка. Если f ^' (x) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную  f ^' (x) в окрестности точки x_о и вторую производную   в самой точке x_о. Если f ^' (x_о) = 0,  >0 ( <0), то точка x_оявляется точкой локального минимума (максимума) функции f(x). Если же  =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

15. Условные экстремумы. Пусть функция  z=f(x,y) определена в некоторой области    и в этой области задана кривая уравнением φ(x,y)=0. Условным экстремумом функции двух переменных z=f(x,y) называют ее экстремум при условии, что точки берутся на заданной кривой. Если из уравнения кривой можно, например, выразить y=y(x), то задача о нахождении условного экстремума сводится к исследованию на экстремум функции одной переменной z=f(x,y(x)).

Метод множителей Лагранжа. Если уравнение φ(x,y)=0  не разрешимо ни относительно  y=y(x), ни относительно x=x(y), то рассматривают функцию Лагранжа L(x,y,λ)=f(x,y)+λφ(x,y). Необходимым условием существования условного экстремума функции z=f(x,y) при условии φ(x,y)=0 является равенство нулю всех частных производных функции Лагранжа:    .

16. Касательной плоскостью к поверхности   в данной точке P (x₀, y₀, z₀) называется плоскость, проходящая через точку Р и содержащая в себе все касательные, построенные в точке Р ко всевозможным кривым на этой поверхности, проходящим через точку Р.Пусть поверхность s задана уравнением F (х, у, z) = 0 и точка  P (x₀, y₀, z₀) принадлежит этой поверхности.

– уравнение касательной плоскости, построенной в точке P (x₀, y₀, z₀) к поверхности s , заданной уравнением F(х, у, z) = 0;

Нормалью к поверхности s в точке Р называется прямая, проходящая через точку Р и перпендикулярная к касательной плоскости, построенной в этой точке.

– уравнение нормали, построенной в точке Р к поверхности s .

17. Производная по направлению: Предел отношения     при  , если он существует, называется производной функции z=f(x,y) в точке M(x,y) по направлению i и обозначается  . Таким образом:

Производная   характеризует изменения функции в направлении i. При заданных направляющих косинусах производная по направлению вычисляется по формуле

.

Определение 2. Градиентом функции z=f(x,y) в точке M(x,y) называется вектор, координаты которого равны соответствующим частным производным   и  , взятым в точке M(x,y) и обозначается  .

Для случая трёхмерного пространства градиентом скалярной функции   координат  x,y,z  называется векторная функция с компонентами

,  ,  .

Или, использовав для единичных векторов по осям прямоугольных декартовых координат  :

18. Двойной интеграл - это обобщение определенного интеграла на двумерный случай. Т.е. для определения понятия двойного интеграла используется функция, зависящая уже от двух переменных: f(x,y). Эта функция должна быть определена на некоторой, обладающей конечной площадью, области D плоскости X0Y. При этом граница области D должна состоять из конечного числа графиков непрерывных функций.       

Обозначение двойного интеграла

Теорема о существовании двойного интеграла

Если функция от x, y непрерывна в замкнутой области Д, то двойной интеграл существует и не зависит от способов разбиения и выбора точки в каждой элементарной области.

Свойства: