3. Расчёт определителей второго и третьего порядка:

Определителем второго порядка называется число:

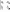
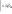
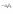
Определителем третьего порядка называется число, полученное при расчёте определителя по формуле Сарруса:

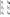
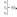
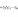
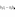
4. Свойства определителей:

1.Определитель не изменится, при замене всех его строк соответствующими столбцами (при транспонировании).

2.При перестановке двух столбцов (строк) местами определитель меняет знак на противоположный.

3.Определители с двумя одинаковыми столбцами (строками) всегда равен нулю.

4.Множитель, общий для элементов некоторого столбца (строки) можно выносить за знак определителя. За знак определителя можно выносить общий множитель любой строки (столбца) любой матрицы, за знак которой можно выносить общий множитель всех элементов.

5.Определитель равен нулю, если все элементы некоторого столбца (строки) равны нулю.

6.Определитель с двумя пропорциональными столбцами (строками) всегда равен нулю.

7.Если в определителе все элементы некоторого столбца (строки) равны суммам двух слагаемых, то такой определитель равен сумме двух соответствующих определителей.

8.Определитель не изменится, если к элементам некоторого столбца (строки) прибавить соответствующие элементы другого столбца (строки), предварительно умножив их на один и тот же коэффициент.

9.Минором М_ij элемента а_ij матрицы n-ного порядка называется определитель матрицы (n-1)-го порядка, получаемой из матрицы n-ного порядка путём вычёркивания i-строки и j-столбца.

Каждая матрица n-ного порядка имеет n² миноров n-первого порядка.

10.Алгебраическим дополнением А_ij элемента а_ij называется минор элемента a_ij умноженный на (-1)^i+j

Дополнение всегда обозначают той же буквой, что и матрица, но всегда с индексами.

11.Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

12. Определитель произведения двух квадратных матриц равен произведению их определителей.

13. Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения другой строки (столбца) всегда равна нулю.

5. Обратная матрица. Теорема (необходимое и достаточное условие существования обратной матрицы). Алгоритм вычисления обратной матрицы методом Гаусса.

Обратной для квадратной матрицы А называется матрица А^-1, для которой выполняется: А^-1*А=А*А^-1=Е

Из определения следует, что обратную матрицу можно построить только для квадратной, обе матрицы прямая и обратная имеют один и тот же порядок.

Необходимое и достаточное условие существования обратной матрицы:

Определитель прямой матрицы должен быть отличен от нуля. Тогда матрица А называется не вырожденной или не особенной. В противном случае, если определитель равен нулю, матрица называется вырожденной или особенной.

Теорема:

Обратная матрица А^-1 существует и единственна тогда и только тогда, когда исходная матрица не вырождена.

Необходимость.

Пусть для матрицы А существует обратная А^-1, т.е. А* А^-1 = А^-1*А = Е. Тогда, |А* А^-1|=|А|*|А^-1|=|Е|=1,т.е.|А| ≠ 0 и |А^-1| ≠ 0; А – невырожденная.

Достаточность.

Пусть дана невырожденная матрица порядка n

,

так что ее определитель 0. Рассмотри матрицу, составленную из алгебраических дополнений к элементам матрицы А:

,

ее называют присоединенной к матрице А.

Следует обратить внимание на то, что алгебраические дополнения к элементам i-той строки матрицы А стоят в i-том столбце матрицы А^*, для .

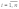Найдем произведения матриц АА^* и А^*А. Обозначим АА^* через С, тогда по определению произведения матриц имеем: С_ij = а_i1А _1j + а_i2А _2j + … + а_inА_nj ;

При i = j получим сумму произведений элементов i - той строки на алгебраические дополнения этой же строки, такая сумма равняется значению определителя. Таким образом С_ij = |А| = D - это элементы главной диагонали матрицы С. При i  j, т.е. для элементов С_ij  вне главной диагонали матрицы С, имеем сумму произведений всех элементов некоторой строки на алгебраические дополнения другой строки, такая сумма равняется нулю. Итак,  = АА^*

Аналогично доказывается, что произведение А на А^* равно той же матрице С. Таким образом, имеем А^*А = АА^* = С. Отсюда следует, что

Поэтому, если в качестве обратной матрицы взять 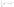, то  Итак, обратная матрица существует и имеет вид:

.

Вычисление обратной матрицы методом Гаусса:

Алгоритм вычисления обратной матрицы методом Гаусса состоит в следующем действии: (А|E) = (E|A^-1), которое проводится посредством тех же операций, что и при вычислении определителя или посредством преобразований Гаусса.