
- •32. Теплопроводность в однослойной плоской стенке.
- •33. Теплопроводность в многослойной плоской стенке. Эквивалентный коэффициент теплопроводности.
- •34. Теплопроводность в однослойной цилиндрической стенке.
- •35. Теплопроводность в многослойной цил.Стенке.
- •36. Теплопередача ч/з однослойн.Плоскую стенку.
- •37. Теплопередача ч/з многослойную плоскую стенку.
- •7) Слои прилегают друг к другу идеально
- •38. Теплопередача через однослойную цилиндр.Стенку.
- •39. Теплопередача через многосл.Цил.Стенку.
- •41. Теплопередача через оребрённую стенку.
- •42. Теплопроводность при нестационарном режиме.
- •43. Конвективный теплообмен. Виды движения теплоносителя. Факторы, влияющие на процесс конвективного теплообмена. Тепловой и даинамический пограничный слой.
- •44. Подобие физических процессов. Критерии подобия. Критериальные уравнения. Теоремы подобия.
- •45. Теплоотдача при свободном движении теплоносителя в трубах.
- •46. Теплообмен при вынужденном движении теплоносителя в трубах.
37. Теплопередача ч/з многослойную плоскую стенку.
1) δ<<l
2) λ=const
3) g(вектор)=const
4) Тс1=const
Tc2=const
5) T=f(x)
6)
7) Слои прилегают друг к другу идеально
![]() -многослойкая
плоск.стенка
-многослойкая
плоск.стенка
![]() -полный
термич.коэф.
-полный
термич.коэф.
![]() -коэф.теплопередачи
однослойной или многосл.плоской стенки.
-коэф.теплопередачи
однослойной или многосл.плоской стенки.
K показывает какое кол-во теплоты проходит ч/з еденицу площади поверхности стенки в ед.вр. от горячего ист. к хол. При разности t-р =1.
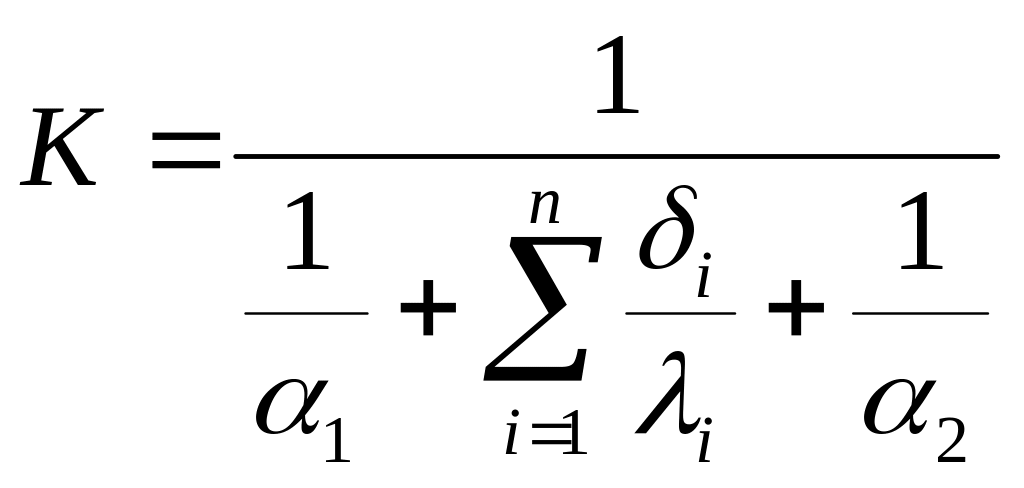
38. Теплопередача через однослойную цилиндр.Стенку.
1) -стенка однородная
2) r2 >r1
r2-r1=δ<<l
3) Тс1=const
Tc2=const
4) g(вектор)=const
5)
![]() -уравнение
Ньютона-Рихмана
-уравнение
Ньютона-Рихмана
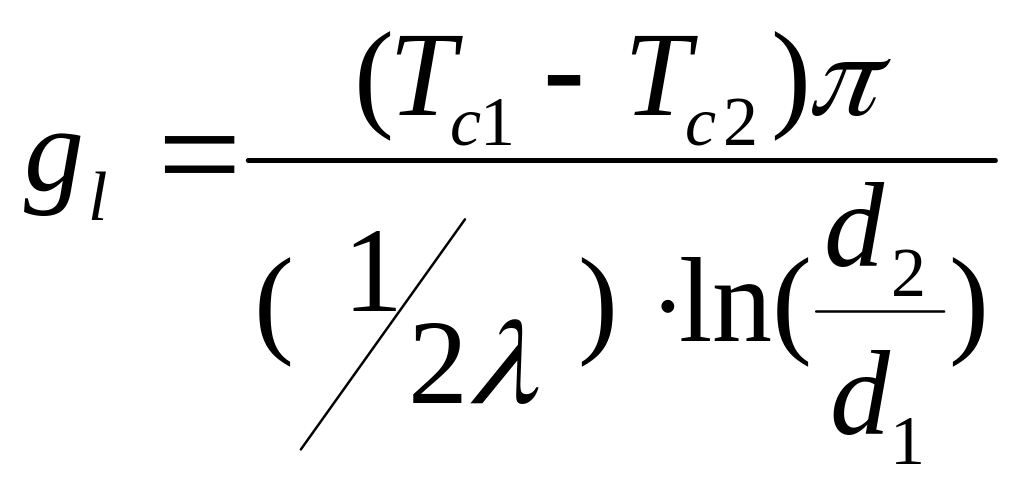
![]()
![]()
![]()
![]()
![]()
полное термическое сопротивление односл.цил.стенки.
![]()
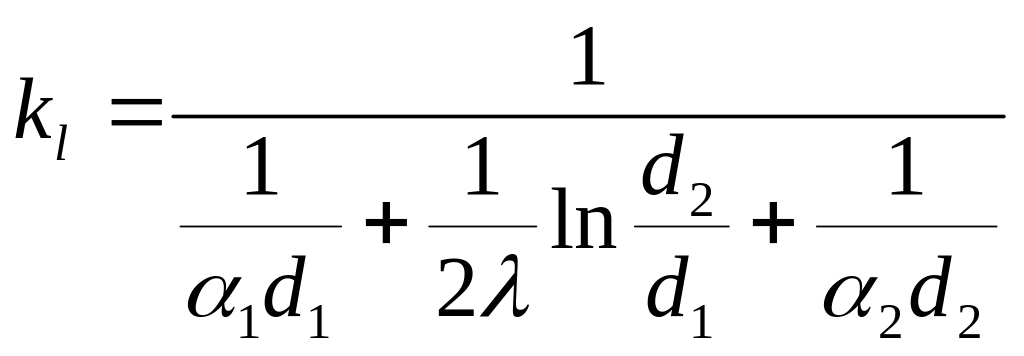
![]()
![]()
39. Теплопередача через многосл.Цил.Стенку.
1) -стенка однородная
2) r2 >r1
r2-r1=δ<<l
3) Тс1=const
Tc2=const
4) g(вектор)=const
5)
6) прилигание слоёв идеальное
7) материалы однородные, но
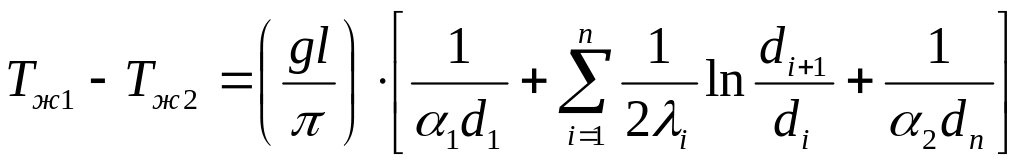
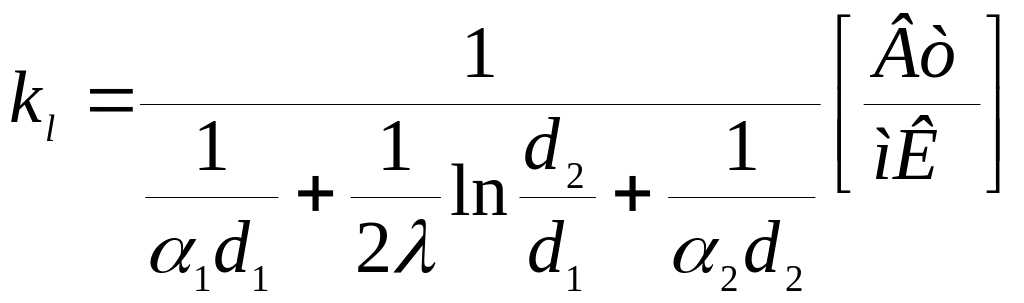 линейный коэффициент
теплопередачи, характеризует
интенсивность передачи теплоты от одной
жидкости к другой через разделяющую их
стенку; численно равен количеству
теплоты, которое проходит от одной среды
к ругой через стенку трубы длиной 1м в
единицу времени при разности температур
между ними в 1К.
линейный коэффициент
теплопередачи, характеризует
интенсивность передачи теплоты от одной
жидкости к другой через разделяющую их
стенку; численно равен количеству
теплоты, которое проходит от одной среды
к ругой через стенку трубы длиной 1м в
единицу времени при разности температур
между ними в 1К.
Величина, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередаче.
41. Теплопередача через оребрённую стенку.
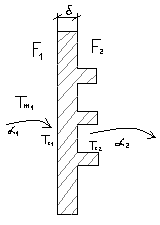 Рассмотрим оребренную
стенку с толщиной
и теплопроводностью .
С гладкой стороны площадь поверхности
равна F1,
а с оребренной – F2.
заданы постоянные во времени температуры
tж1
и tж2,
а также коэффициенты теплоотдачи 1
и 2.
Рассмотрим оребренную
стенку с толщиной
и теплопроводностью .
С гладкой стороны площадь поверхности
равна F1,
а с оребренной – F2.
заданы постоянные во времени температуры
tж1
и tж2,
а также коэффициенты теплоотдачи 1
и 2.
g(вектор)=const
![]()
![]()
![]()
![]()

![]()
![]()
Полное термическое сопротивление оребрённой плоской стенки.
![]()
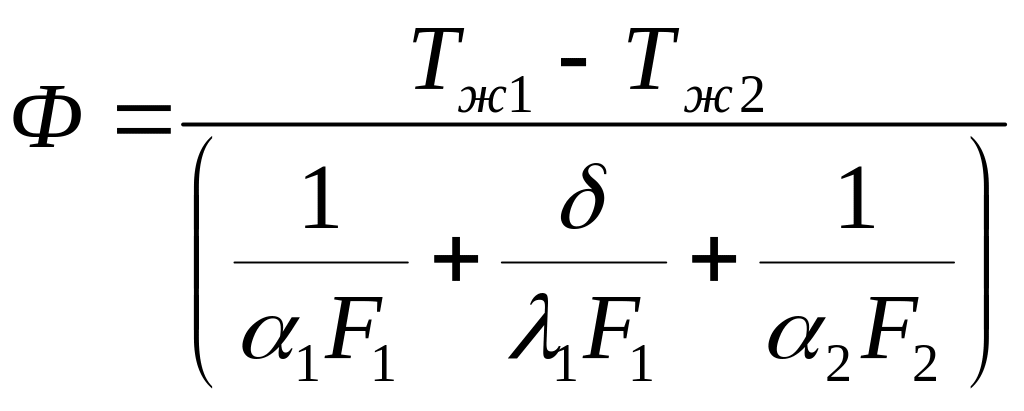
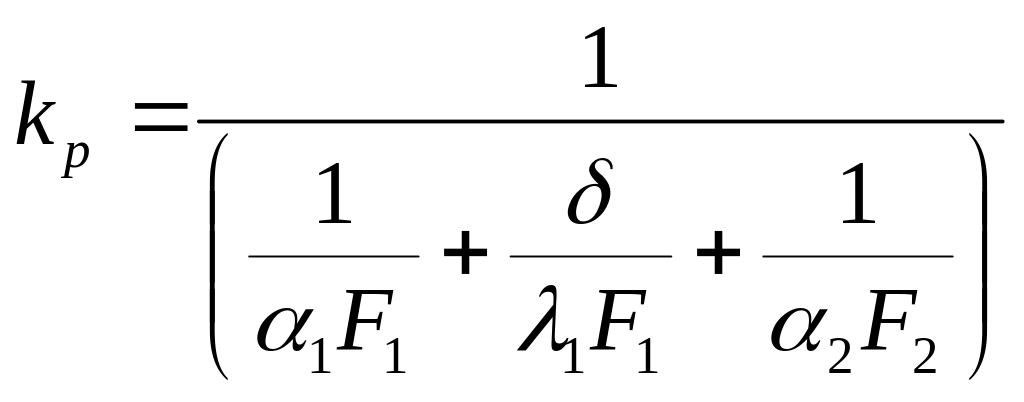
– коэффициент теплопередачи для оребренной стенки.
При расчете плотности
теплового потока на единицу неоребренной
поверхности стенки получим:
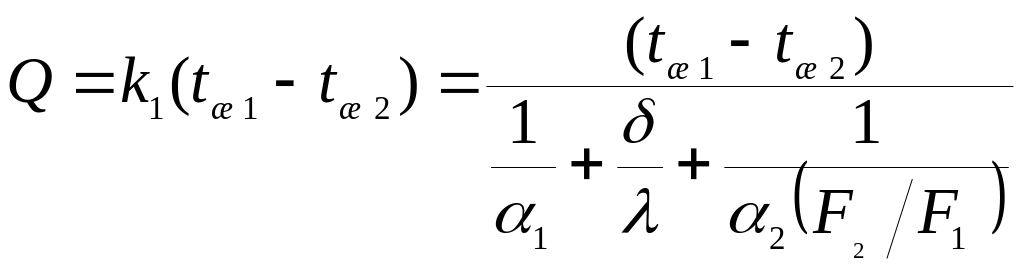 .
k1
– коэффициент теплопередачи, отнесенный
к неоребренной поверхности стенки.
.
k1
– коэффициент теплопередачи, отнесенный
к неоребренной поверхности стенки.
Отношение площади оребренной поверхности к площади гладкой поверхности F2/F1 называется коэффициентом оребрения.
42. Теплопроводность при нестационарном режиме.
Нестационарная теплопроводность – процесс при котором температура в заданной точке твердого тела изменяется во времени совокупность указанных температур образует нестационарное температурное поле, нахождение которого и является основной задачей нестационарной теплопроводности.
Задачу об отыскании
трехмерного температурного поля можно
сформулировать в соответствии принципами,
изложенными в разделе «математическая
формулировка задач теплообмена».
Формулировка задачи включает уравнение
теплопроводности:
![]() ,
где
,
где
![]() – коэффициент температуропроводности
м2/с,
а также условия однозначности, позволяющие
выделить единственное решение из
множества решений уравнения, различающихся
значением констант итегрирования.
– коэффициент температуропроводности
м2/с,
а также условия однозначности, позволяющие
выделить единственное решение из
множества решений уравнения, различающихся
значением констант итегрирования.
Условия однозначности включают начальные и граничные условия. Начальные условия задают значения искомой функции t в начальный момент времени по всей области D. В качестве области D, в которой необходимо найти температурное поле, будем рассматривать прямоугольный параллелепипед с размерами 2, 2ly, 2lz, например, элемент строительной конструкции. Тогда начальные условия можно записать в виде: при =0 и -х; - lyуly; -lzzlz имеем t = t(x, y, z,0) = t0(x, y, z). Из этой записи видно, что начало декартовой системы координат расположено в центре симметрии параллелепипеда.
Граничные условия
сформулируем в форме граничных условий
III
рода, часто встречающихся на практике.
Граничные условия III
рода задают для любого момента времени
на границах области D
коэффициент теплоотдачи и температуру
окружающей среды. В общем случае на
различных участках поверхности S
области D
эти величины могут быть различными. Для
случая одинакового коэффициента
теплоотдачи
на всей поверхности S
и всюду одинаковой температуры окружающей
среды tж
граничные условия III
рода при
>0 можно записать в виде:
![]() ;
;
![]() ;
;
![]()
где
![]() .
S
– поверхность, ограничивающая область
D.
.
S
– поверхность, ограничивающая область
D.
Температура в каждом из трех уравнений берется на соответствующей грани параллелепипеда.
Рассмотрим аналитическое решение сформулированной выше задачи в одномерном варианте, т.е. при условии ly,lz ». В этом случае требуется найти температурное поле вида t = t(x, ). Запишем формулировку задачи:
уравнение
![]() ;
;
начальное условие: при = 0 имеем t(x, 0) = t0 = const;
граничное условие:
при x
= ,
> 0 имеем
![]() .
.
В соответствии с этими выражениями имеется бесконечная пластина толщиной 2, изготовленная из материала с коэффициентом темературопроводности а и обладающая в начальный момент времени температурой t0. пластина резко переносится в среду с температурой tж и коэффициентом теплоотдачи . С этого момента температура в пластине изменяется так, чтобы удовлетворялось уравнение . Задача состоит в том, чтобы получить конкретную формулу t = t(x, ), позволяющую найти температуру t в любой точке пластины в произвольный момент времени.
Сформулируем задачу
в безразмерных переменных, это позволит
сократить записи и сделает решение
более универсальным. Безразмерная
температура равна
![]() ,
безразмерная координата равна Х = х/.
Подставив эти величины в уравнение
получим
,
безразмерная координата равна Х = х/.
Подставив эти величины в уравнение
получим
![]() ,
где
,
где
![]() - число Фурье
(безразмерное
время).
- число Фурье
(безразмерное
время).
Начальное условие запишется в следующем виде: Fo = 0; = 1.
Граничное условие
запишется как: Fo
> 0; Х =1;
![]() ,
где
,
где
![]() – число Био.
– число Био.
Формулировка задачи в безразмерном виде содержит единственный параметр – число Био, которое в данном случае является критерием, так как составлено только из величин, входящих в условие однозначности. Использование числа Био связано с нахождением температурного поля в твердом теле, поэтому в знаменателе Bi – теплопроводность твердого тела. Bi – наперд заданный параметр и является критерием.
Если рассматривать 2 процесса нестационарной теплопроводности с одинаковыми числами Био, то, согласно третьей теореме подобия, эти процессы подобны. Это значит, что в сходственных точках (т.е. при Х1=Х2; Fo1=Fo2) безразмерные температуры будут численно равны: 1=2. следовательно, произведя один расчет в безразмерном виде, мы получим результат, справедливый для класса подобных явлений, которые могут различаться размерными параметрами t0 и tж.
