
- •Комплексные числа. Геометрическая интерпретация комплексных чисел.
- •13. Обыкновенные дифференциальные уравнения первого порядка. Задача Коши. Теорема Коши. Общее и частное решения.
- •Дифференциальные уравнения первого порядка: с разделенными переменными, с разделяющимися переменными, однородные, линейные, уравнения Бернулли.
- •Дифференциальные уравнения высших порядков. Задача Коши. Теорема Коши.
- •Дифференциальные уравнения высших порядков, допускающие понижение порядка.
- •Линейная зависимость и линейная независимость системы функций. Определитель Вронского. Необходимое условие линейной зависимости системы функций.
- •Линейный дифференциальный оператор. Свойства решений однородных линейных дифференциальных уравнений п - го порядка.
- •Необходимое и достаточное условие линейной независимости частных решений однородных линейных дифференциальных уравнений п - го порядка.
- •Структура общего решения однородных и неоднородных линейных дифференциальных уравнений n - го порядка.
- •Метод вариации произвольных постоянных.
- •Решения однородных линейных дифференциальных уравнения п - го порядка с постоянными коэффициентами в зависимости от корней характеристического уравнения.
- •Метод подбора частного решения неоднородных линейных дифференциальных уравнений п - го порядка. Метод суперпозиции решений.
- •Двойные интегралы и их свойства. Теорема о среднем. Вычисление двойных интегралов в декартовой системе координат.
- •Полярная система координат. Переход в двойных интегралах от декартовой системы координат к полярной системе координат. Вычисление двойных интегралов в полярной системе координат.
- •Приложения двойных интегралов.
- •Тройные интегралы и их свойства. Теорема о среднем. Вычисление тройных интегралов в декартовых координатах.
- •Криволинейные координаты в пространстве. Переход в тройных интегралах от декартовой системы координат к криволинейной системе координат.
- •Цилиндрическая система координат. Вычисление тройных интегралов в цилиндрической системе координат.
- •Сферическая система координат. Вычисление тройных интегралов в сферической системе координат.
- •Приложения тройных интегралов.
- •Криволинейные интегралы первого и второго рода. Формула Грина.
- •Поверхностные интегралы первого и второго рода. Формула Остроградского - Гаусса.
- •Векторные функции скалярного аргумента.
- •Скалярное поле. Поверхности уровня, линии уровня.
- •Производная по направлению. Градиент скалярного поля.
- •Векторное поле. Векторные линии.
- •Поток векторного поля. Дивергенция векторного поля. Векторная запись формулы Остроградского - Гаусса.
- •Линейный интеграл. Циркуляция векторного поля.
Сферическая система координат. Вычисление тройных интегралов в сферической системе координат.
(x,y,z) – корд в д.с.к. т.М. М(φ,θ,r) – корд в сферич с.к. 0≤φ≤2π, 0≤θ≤π, 0 ≤r<+∞. Ф-лы связи межд д.с.к и сферическими: {x=rsinθcosφ, {y=rsinθsinφ, {z=rcosθ; Исследуем: 1) φ=С {x=rsinθcosС, {y=rsinθsinС, {z=rcosθ; исключаем r,θ y/x=tgC, y=xtgC – сем-во пл-тей, проходящих ч/з ось аппликат(oz). 2) θ=С {x=rsinСcosφ, {y=rsinСsinφ, {z=rcosС; Исключаем r и φ {x2+y2=r2sin2C {r=z/cosC, x2+y2=z2*sin2C /cos2C x2+y2=z2tg2C -сем-во конич пов-й с осью oz. 3) r=C {x=Сsinθcosφ, {y=Сsinθsinφ, {z=Сcosθ; x2+y2+z2=C2 – cем-во концентрич сфер в центре –нач-ле координат.
☼ Определитель
3го порядка вида: J(φ,θ,r)=
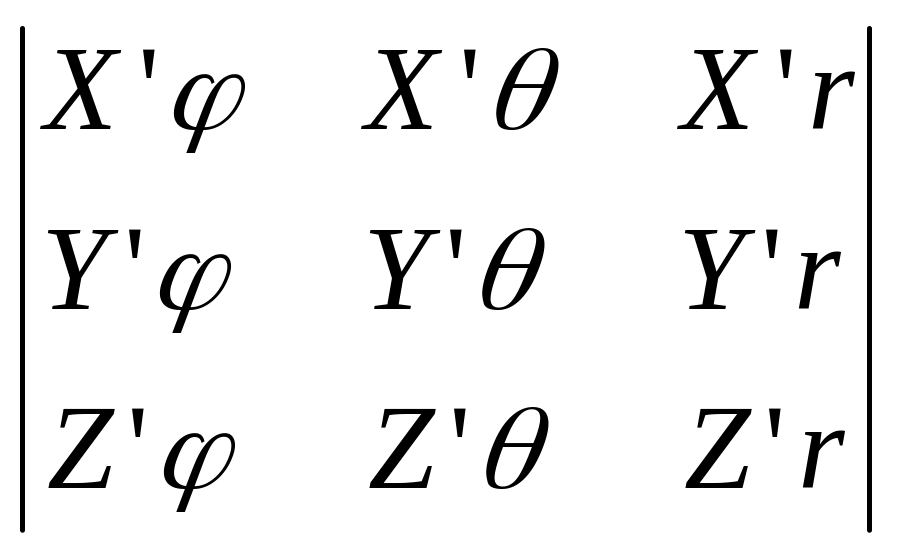 - якобиан перехода от д.с.к. к сферической.
Имеем: J(φ,θ,r)=
- якобиан перехода от д.с.к. к сферической.
Имеем: J(φ,θ,r)= =
|расклад по 3й строке| = rsinθ
=
|расклад по 3й строке| = rsinθ +cosθ
+cosθ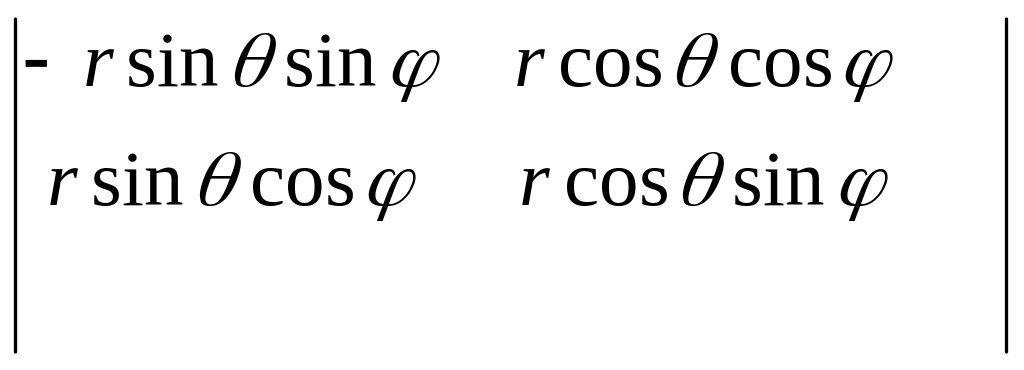 =
rsinθ(-rsin2θsin2φ
–rsin2θcos2φ)
+cosθ(-rsinθcosθsinφ
–r2sinθcos2φ)=
-rsin3θ
–r2sinθcos2θ=
-r2sinθ.
J(φ,θ,r)=
-r2sinθ.
|J(φ,θ,r)|=r2sinθ
– якобиан перехода от д.с.к. к сферич.
f(x,y,z)dxdydz=
=
rsinθ(-rsin2θsin2φ
–rsin2θcos2φ)
+cosθ(-rsinθcosθsinφ
–r2sinθcos2φ)=
-rsin3θ
–r2sinθcos2θ=
-r2sinθ.
J(φ,θ,r)=
-r2sinθ.
|J(φ,θ,r)|=r2sinθ
– якобиан перехода от д.с.к. к сферич.
f(x,y,z)dxdydz=
![]() f(rsinθcosφ,
rsinθsinφ,
rcosθ)*r2sinθ
dφdθdr
- ф-ла перехода от дек коорд к сферическим.
f(rsinθcosφ,
rsinθsinφ,
rcosθ)*r2sinθ
dφdθdr
- ф-ла перехода от дек коорд к сферическим.
Приложения тройных интегралов.
1) VT= dxdydz
2) m= μ(x,y,z)dxdydz, μ=μ(x,y,z) – пл-ть распред массы по телу V. Зам-е: если тело однор, то μ=const.
3) Статические моменты относительно корд пл-тей
MXY= z μ(x,y,z)dxdydz
MXZ= y μ(x,y,z)dxdydz
MYZ= x μ(x,y,z)dxdydz
4)xC=
![]() x
μ(x,y,z)dxdydz
/
μ(x,y,z)dxdydz,
x
μ(x,y,z)dxdydz
/
μ(x,y,z)dxdydz,
yC= y μ(x,y,z)dxdydz / μ(x,y,z)dxdydz,
zC= z μ(x,y,z)dxdydz / μ(x,y,z)dxdydz,
5) Момент инерции
1) Относит нач корд:
J0= (x2+y2+z2)μ(x,y,z)dxdydz,
2)Относит осей коорд
JX= (y2+z2)μ(x,y,z)dxdydz,
Jy= (x2+z2)μ(x,y,z)dxdydz,
JZ= (x2+y2)μ(x,y,z)dxdydz,
3)Относит пл-тей коорд
JXY= z2 μ(x,y,z)dxdydz,
JXZ= y2 μ(x,y,z)dxdydz,
JYZ= x2 μ(x,y,z)dxdydz,
Криволинейные интегралы первого и второго рода. Формула Грина.
☼ Кривая называется спрямляемой, если в любой ее точке можно провести касательную, непрерывно изменяющуюся вдоль всей ее кривой.
Берем спрямляемую без т самопересчения кривую AB. Пусть на АВ определена ф-я f(P), тР (АВ). Произв образом разбиваем АВ на n элемент кривых точками Р0=А,Р1, …,Рn=В. (Рk-1,Pk), k=1,n - элемент кривые. Длина эл кривой ∆lk, k=1n. Выбираем наиб длину кривой, max(∆lk)=λ. Произвольным образом на кажд кривой выбираем точку Мk (Pk-1,Pk), k=1n и вычисляем значение: f(Mk), k=1n. Составл произведение f(∆Mk) ∆lk, k=1n.
f(M1)
∆l1+f(M2)
∆l2+…+f(Mn)
∆ln=![]() (1)
Сумма (1)
– интегр сумма для криволин инт 1 рода
для ф-и f(P)
по кривой АВ. Будем неогранич увеличивать
число элемент кривых, чтобы они стягивались
в точку.
(1)
Сумма (1)
– интегр сумма для криволин инт 1 рода
для ф-и f(P)
по кривой АВ. Будем неогранич увеличивать
число элемент кривых, чтобы они стягивались
в точку.
☼Если при стремлении
к 0 наибольшей из длин элем кривых
существует конечный предел интегральной
суммы (1),
к-й не зависит ни от способа разбиения
кривой АВ на элементарные, ни от выбора
точек на элемент кривых, то он называется
- криволин
инт 1 рода для ф-и f(P)
по кривой АВ и обозначается следующим
образом:
![]() .
.
Получили:
![]() =
Зам-я: 1)
Аналогичный процесс может быть применен
и в случае замкнутой кривой, если за т.
Р0(или
Рn)
выбрать любую т кривой, а ост т Рk
располагать в соответствии с выбранным
направлением на кривой. 2) Опр крив инт
1 рода не связано с выбором сист корд,
поэтому оно инвариантно. Если в пр-ве
задана д.с.к, то ф-я f(P)
становится ф-й f(x,y,z).
Тогда предел
=
Зам-я: 1)
Аналогичный процесс может быть применен
и в случае замкнутой кривой, если за т.
Р0(или
Рn)
выбрать любую т кривой, а ост т Рk
располагать в соответствии с выбранным
направлением на кривой. 2) Опр крив инт
1 рода не связано с выбором сист корд,
поэтому оно инвариантно. Если в пр-ве
задана д.с.к, то ф-я f(P)
становится ф-й f(x,y,z).
Тогда предел
![]() =
=![]() ,
где MK(xK,yK,zK)
(Pk-1,Pk),k=1n.
Если крив АВ – плоская, то ф-я 2х переем
f(x,y),
тогда
,
где MK(xK,yK,zK)
(Pk-1,Pk),k=1n.
Если крив АВ – плоская, то ф-я 2х переем
f(x,y),
тогда
![]() =
=![]()
Теор Необх усл-е существ криволин инт 1 рода: Если ф-я f(P) интегрируема на спрямляемой, без т. самопересечения кривой АВ, то она ограничена на этой кривой.
Теор Дост усл сущ-я крив инт 1 рода: Если ф-я f(P) непр на спрям, без т. самопер крив АВ, то она интегрируема на эт кривой.
Физич смысл кривол инт 1 рода: Если ф-я f(P) выражает пл-ть распределения массы вдоль кривой АВ, то кривол инт 1 рода от этой ф-и есть масса кривой АВ. MAB=
Зам-я: 1) Св-ва крив
инт 1 рода аналогичны св-вам 2х и 3х
интегралов. 2) Крив инт 1 рода не
зависит от
направления кривой.
=![]() 3) Если подинтегральн ф-я= 1 на всей
кривой, то крив инт на АВ = длине этой
кривой
3) Если подинтегральн ф-я= 1 на всей
кривой, то крив инт на АВ = длине этой
кривой
![]() =lAB.
4)
Теор о среднем
Если ф-я f(P)
непр, спрямл, без т. самопересечения на
крив АВ, то найдется такая т Р, что крив
инт этой ф-и=значению этой ф-и в т Р на
длину кривой.
=f(P’)lAB.
Вычисл крив инт 1 рода Т1
Если выполн усл: 1) ф-я f(x,y,z)
непр на спрямл, без . самопересеч крив
АВ, 2) крив АВ задана параметрически
{x=φ(t),
{y=ψ(t),
{z=h(t),
t
[α,β].
Причем, когда t
пробегает отрезок [α,β] соотв значения
x,y,z
пробегают АВ. 3) φ(t),
ψ(t),
h(t)
– имеют непр произв на АВ, то криволин
интеграл 1 рода сводится к определенному
интегралу:
=lAB.
4)
Теор о среднем
Если ф-я f(P)
непр, спрямл, без т. самопересечения на
крив АВ, то найдется такая т Р, что крив
инт этой ф-и=значению этой ф-и в т Р на
длину кривой.
=f(P’)lAB.
Вычисл крив инт 1 рода Т1
Если выполн усл: 1) ф-я f(x,y,z)
непр на спрямл, без . самопересеч крив
АВ, 2) крив АВ задана параметрически
{x=φ(t),
{y=ψ(t),
{z=h(t),
t
[α,β].
Причем, когда t
пробегает отрезок [α,β] соотв значения
x,y,z
пробегают АВ. 3) φ(t),
ψ(t),
h(t)
– имеют непр произв на АВ, то криволин
интеграл 1 рода сводится к определенному
интегралу:
![]() =
=![]()
![]()
Т2
Если выполн усл-я: 1) ф-я f(x,y)
непр на спрямл, без . самопересеч крив
АВ, 2) крив АВ задана параметрически
{x=φ(t),
{y=ψ(t),
t
[α,β].
Причем, когда t
пробегает отрезок [α,β] соотв значения
x,y
пробегают АВ. 3) φ(t),
ψ(t)
– имеют непр произв на [α,β], то криволин
интеграл 1 рода для ф-и сводится к
определенному интегралу:
![]() =
=![]()
![]() зам-я: если крив АВ задана ур-м, разрешимым
относительно одной из переменных, н-р,
y=g(x),
x
[a,b],
то
зам-я: если крив АВ задана ур-м, разрешимым
относительно одной из переменных, н-р,
y=g(x),
x
[a,b],
то
![]() =
=![]()
![]()
Крив инт 2го рода Возьмем плоский случай. Пусть задана спрямляемая, без т самопересечения направленная кривая АВ, определена ф-я f(x,y). Произвольн образом кривую АВ делим на n кривых. Р0=А,Р1, …,Рn=В. (Рk-1,Pk), k=1,n - элемент кривые. Длина эл кривой ∆lk, k=1n. Выбираем наиб длину кривой, max(∆lk)=λ. Произвольным образом на кажд кривой выбираем точку Мk (Pk-1,Pk), k=1n и вычисляем значение: f(Mk), k=1n. Составл произведение f(∆Mk) ∆хk, k=1n, ∆xK=xK-xK-1. Суммируем по всем k
f(M1)
∆х1+f(M2)
∆х2+…+f(Mn)
∆хn=![]() (1)
Сумма (1)
– интегр сумма ф-и f(x,y)
на напрявленной кривой АВ по коорд х.
☼Если при стремлении к 0 наиб из длин
кривых λсуществует конечный предел
интегральной суммы (1),
не зависящий ни от способа разбиения,
ни от выбора точек на кажд элент крив,
то он наз-ся
криволинейн интеграл 2 рода для
ф-и f(x,y)
по направленной
кривой АВ и координате х, обозначается:
(1)
Сумма (1)
– интегр сумма ф-и f(x,y)
на напрявленной кривой АВ по коорд х.
☼Если при стремлении к 0 наиб из длин
кривых λсуществует конечный предел
интегральной суммы (1),
не зависящий ни от способа разбиения,
ни от выбора точек на кажд элент крив,
то он наз-ся
криволинейн интеграл 2 рода для
ф-и f(x,y)
по направленной
кривой АВ и координате х, обозначается:
![]() =
=![]() .
Аналогично
можно получить по другим координатам:
.
Аналогично
можно получить по другим координатам:
![]() =
=![]() .
Аналогично пространственный случай
f(x,y,z):
по х
.
Аналогично пространственный случай
f(x,y,z):
по х
![]() =
=![]() ,
по у
,
по у
![]() =
=![]() ,
по z
,
по z
![]() =
=![]()
☼Если P(x,y,z,),
Q(x,y,z),
R(x,y,z)
на спрямляем, без т. самопересеч, простр
крив АВ, ф-и определены на крив АВ, тогда
существ:
![]() ,
,
![]() ,
,
![]() ,
то криволин интеграл 2 рода вида:
+
,
то криволин интеграл 2 рода вида:
+![]() +
+![]() - обобщенный
интеграл 2 рода.
- обобщенный
интеграл 2 рода.
Физический смысл
крив инт 2 рода:
Если ф-и P(x,y),
Q(x,y)
– проекции силового поля соотвенно на
оси координат ox,oy,oz,
то
![]() +
+![]() ,
выражает
работу силового поля по перемещению
единицы массы из т. А в т.В, в направлении
кривой АВ.
,
выражает
работу силового поля по перемещению
единицы массы из т. А в т.В, в направлении
кривой АВ.
Вычисление крив
инт 2 рода Т1
Если выполн усл: 1) ф-я f(x,y)
непр на спрямл, без т. самопересеч
направленной
крив АВ, 2) крив АВ задана параметрически
{x=φ(t),
{y=ψ(t),
t
[α,β].
t=α
A,
t=β
B
3) φ(t),
ψ(t),
– имеют непр произв,
![]() =
=
![]() по коорд х,
по коорд х,
![]() =
=![]()
![]() по коорд у
по коорд у
Т2
Если выполн усл-я: 1) ф-я P(x,y),
Q(x,y)
непр на спрямл, без т. самопересеч
направленной
крив АВ, 2) крив АВ задана параметрически
{x=φ(t),
{y=ψ(t),
{z=h(t),
t
[α,β].
t=α
A,
t=β
B
3) φ(t),
ψ(t)
– имеют непр произв на t
[α,β],
то
+
=![]() Вывод:
Кривол инт 2 рода зависит от пути
интегрирования.
Вывод:
Кривол инт 2 рода зависит от пути
интегрирования.
Т3
Если выпоолня усл-я: 1) ф-я P(x,y),
Q(x,y)
непр на спрямл, без т. самопересеч
направленной
крив АВ, 2) крив АВ задана ур-м, разрешенным
относительно 1 из переменных y=g(x);
x
[a,b],
x=a
A,
x=b
B,
3) Ф-я g(x)
– имеет непр произв на АВ, то крив инт
по кривой АВ
+
=![]()
Т4
Если выполн усл-я: 1) ф-я P(x,y,z),
Q(x,y,z),
R(x,y,z)
- непр на спрямл, без т. самопересеч
направленной
крив АВ, 2)
крив АВ задана параметрически {x=φ(t),
{y=ψ(t),
{z=h(t),
t
[α,β].
t=α
A,
t=β
B
3) φ(t),
ψ(t),
h(t)
– имеют непр произв на АВ, то справедливо:
+
+
=![]() [P(φ(t),ψ(t),h(t))φ’(t)+
Q(φ(t),ψ(t),h(t))ψ’(t)+
R(φ(t),ψ(t),h(t))h’(t)]dt
[P(φ(t),ψ(t),h(t))φ’(t)+
Q(φ(t),ψ(t),h(t))ψ’(t)+
R(φ(t),ψ(t),h(t))h’(t)]dt
Ф-ла Грина ☼Направление обхода замкнутого контура – положит, если обл-ть, ограниченная этим контуром лежит слева от наблюдателя. Установим связь между крив инт по замкнутому контуру и двойным интегралом по обл-ти, огранич этим замкнут контуром.
Т Грина: Если
P(x,y)
и Q(x,y)
непр в обл-ти D
и на ее границе ∂D=L,
то справедлива ф-ла:
![]() P(x,y)dx+Q(x,y)dy=
(∂Q/∂x
- ∂P/∂y)dxdy
- формула
Остроградского-Грина
P(x,y)dx+Q(x,y)dy=
(∂Q/∂x
- ∂P/∂y)dxdy
- формула
Остроградского-Грина
Зам-е: 1) Ф-ла Грина позволяет вычислять площадь фигур
2) Пусть ф-я P(x,y), Q(x,y) непр в односвязной обл-ти D. Контур АВ полностью лежит в обл-ти D (AB D), тогда справедлива теорема: Т5 Независимость криволин интегр от пути интегрирования. Для того,чтобы криволин инт не зависил от пути интегрир – необходимо и достаточно выполнение двух условий: 1) ф-и P(x,y) и Q(x,y) непр в обл-ти D 2) частн произв непр в обл-ти D и равны между собой в обл-ти D ∂Q/∂x = ∂P/∂y
3) Для
вычисления интегр не зависящего от пути
интегрирования (важна нач и конечн
точки) в качестве наивыгоднейшего пути
целесообразно брать ломаную соединяющую
эти т (х0,у0)
и (х1,у1),
звенья к-й || осям координат
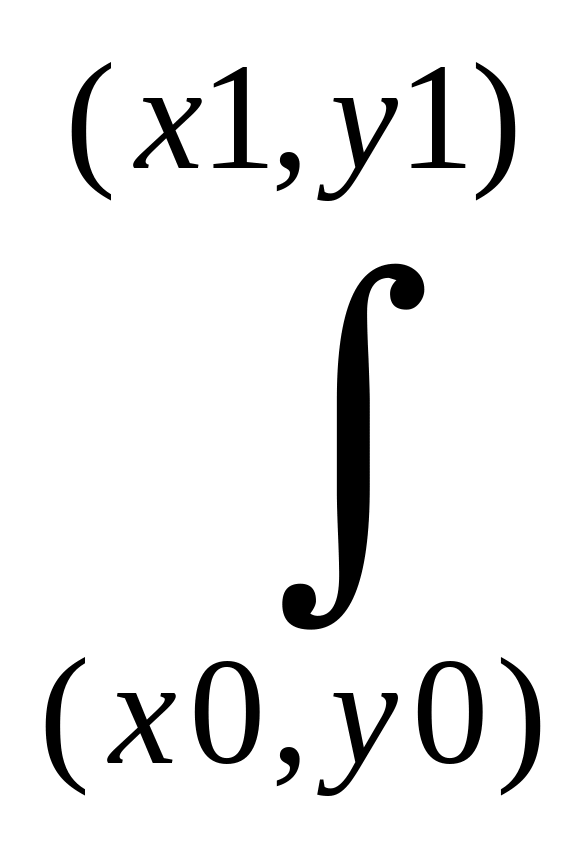 P(x,y)dx+Q(x,y)dy
P(x,y)dx+Q(x,y)dy
4) При указанных
условиях в зам-и 3) подинтегральное
выражение P(x,y)dx+Q(x,y)dy
– является полным диф-алом нек-й ф-и
du(x,y)=
P(x,y)dx+Q(x,y)dy
Ф-ю u(x,y)
– первообразную – можно найти вычисляя
соответств криволин интеграл по ломанной
A0A1B,
где А0(х0,у0)
– произвольная фиксированная т. обл-ти
D.
В(х,у) – переменная точка, А1
–опред по чертежу. u(x,y)=
P(x,y)dx+Q(x,y)dy=![]() P(x,y)dx+Q(x,y)dy
P(x,y)dx+Q(x,y)dy
+![]() P(x,y)dx+Q(x,y)dy=
P(x,y)dx+Q(x,y)dy=![]() P(x,y0)dx+
P(x,y0)dx+![]() Q(x,y)dy,
(А0А1):у=у0,
∂у=0, (А1В):х=const,
dx=0
u(x,y)=
P(x,y0)dx+
Q(x,y)dy+C,
Q(x,y)dy,
(А0А1):у=у0,
∂у=0, (А1В):х=const,
dx=0
u(x,y)=
P(x,y0)dx+
Q(x,y)dy+C,
A0A2B u(x,y)= Q(x0,y)dy+ P(x,y)dx +C.
Теорема 6 Ф-я P(x,y), Q(x,y) непр со своими частн произв 1го порядка в нек-й односвязной обл-ти D, тогда для того,чтобы криволин инт по любому замкн контуру был =0 необх и достаточно, чтобы выполнялось условие: ∂Q/∂x = ∂P/∂y, (х,у) D P(x,y)dx+Q(x,y)dy=0
Связь между
криволин инт 1го и 2го рода. Пусть
ф-и P(x,y),
Q(x,y)
непр на гладкой, направлен кривой АВ.
Т.к. кривая гладкая, то в любой т можно
провести касат, к-я по направлению
совпадает с направлен крив АВ. Обозначим
ч/з α, β углы,к-е образует касат вектор
АВ с осями корд ох,оу. Тогда справедлива
ф-ла:
![]() P(x,y)dx+Q(x,y)dy=
[P(x,y)cosα+Q(x,y)cosβ]dl
- связь между крив инт 1-2 рода,плоский
случай.
P(x,y)dx+Q(x,y)dy=
[P(x,y)cosα+Q(x,y)cosβ]dl
- связь между крив инт 1-2 рода,плоский
случай.
Пусть α, β,γ –углы,к-е составляет касат вектор кривой АВ с соотв осями координат P(x,y,z)dx+Q(x,y,z)dy+ R(x,y,z)dz= [P(x,y,z)cosα+ Q(x,y,z)cosβ+ R(x,y,z)cosγ]dl
Приложения криволин инт 1) =lAB
2) SD=1/2 xdy-ydx Кривая обходится против час стрелки, По ф-ле остр-грина: Пусть P(x,y)=0, Q(x,y)=х (1-0)dxdy= 0dx+xdy= S= xdy. Полагаем, что P(x,y)= -y, Q(x,y)=0 S= - ydx. Сложив почленно и поделив на 2 получим ф-лу SD.
3) Распределение массы: μ= μ(x,y,z) вдоль кривой АВ по длине:
mAB= μ(x,y)dl
4) Коорд центра тяж-ти: xC= x μ(x,y)dl / m, yC= y μ(x,y)dl / m ;
5) Момент инерции J0= (x2+y2) μ(x,y)dl Jx= y2 μ(x,y)dl JY= x2 μ(x,y)dl
6) Работа силы F
по перемещению ед массы из тА в тВ вдоль
направленной кривой АВ. F(x,y)=P(x,y)![]() +Q(x,y)
+Q(x,y)![]() ,
A=
P(x,y)dx+Q(x,y)dy
,
A=
P(x,y)dx+Q(x,y)dy
