20. Метод подбора частного решения неоднородных линейных дифференциальных уравнений п - го порядка. Метод суперпозиции решений.

НЛДУ n-го порялка с пост коэф-ми. Метод подбора.

y⁽ⁿ⁾+a₁y^(n-1)+…+a_ny=f(x) (25) λⁿ+a₁λ^n-1+…+a_n=0 (7) y_OH=y_OO+y_ЧН С помощью метода вариаций частное неоднородное. В отдельном случае его можно находить методом подбора, если правая часть – вид многочлена 1) L[y]=P_n(x) y_ЧН=(A₀xⁿ+A₁x^n-1+…+A_n)x^s, s – число,показывающее сколько раз 0-корень ур-я 2) L[y]=P_n(x)e^αx y_ЧН=(A₀xⁿ+A₁x^n-1+…+A_n)e^αxx^S, s – число, к-е означает сколько раз число λ встречается среди корней хар ур-я (7) 3) L[y]=e^αx [P_n(x)sin βx+Q_m(x)cos βx], y_ЧН=e^αx[(A₀xⁿ+…+A_n)sin βx+(B₀xⁿ+..+B_n)cos βx]x^S, выберем наибольш степень max(m,n)=n, m≤n. s – число, к-е означает сколько раз пара компл сопряж чисел α±iβ встречается среди корней характер ур-я.

Т Метод наложения (суперпозиции) решений. Если y₁- частн реш L[y]=f₁(x), y₂ – частн решение L[y]=f₂(x), у_n – частн решение неоднор ур-я L[y]=f_n(x), то y=y₁+y₂+…+y_n L[y]=f₁(x)+f₂(x)+…+f_n(x).

20. Двойные интегралы и их свойства. Теорема о среднем. Вычисление двойных интегралов в декартовой системе координат.

Рассм ф-ю 2х переменных с областью определения D. z=f(x,y), D Произвольным образом произвольными кривыми разобьем область Dна n элементарных областей. (∆S₁), (∆S₂)…( ∆S_n). Площадь каждой ∆S₁, ∆S₂… ∆S_n , диаметр - d₁,d₂,…d_n.

☼Диаметром области называется наибольшее из расстояний между двумя точками лежащими на границе области и обзначается d.

В кажд элем обл-ти выбираем диаметр, наибольший из них – d. max(d₁,d₂,…,d_n)=d Произв образом в кажд элем обл-ти ∆S_k выбираем т M_k(x_k,y_k) (∆S_k), k=1,n. И вычисл знач ф-и в этих т. f(x_k,y_k), k=1,n. f(x_k,y_k)*∆S_k , k=1,n. Суммируем по всем k. f(x₁,y₁) ∆S₁+f(x₂,y₂) ∆S₂+…+f(x_n,y_n) ∆S_n= (1) Сумма (1) интегральная сумма для ф-и f(x,y) по области D.

☼Если при стремлении к нулю наибольшего из диаметров d существуют конечный предел интегральной суммы (1) и этот предел не зависит ни от способа разбиения области D на элемнтарные, ни от выбора точек в кажд элемент обл-ти, то этот предел наз-ся – двойным интегралом для ф-и f(x,y) по области D = .

☼Обл D – квадрируемая, если она имеет площадь.

Т Необх условие существ двойного интеграла.

Если ф-я 2х переменных f(x,y) интегрируема в ограниченной замкнутой квадрируемой обл-ти D, то ф-я ограничена в этой обл-ти.

Т Дост усл сущ двойн интегр (∫∫) Если ф-я 2х переем f(x,y) непр в огр, замкн, квадрир обл-ти D, то она интегрируема в этой обл-ти. Зам-е: В дальнейшем будем рассматривать только квадрируемые обл-ти.

Пусть ф-я f(х,у) неотрицательна и определена в обл-ти D. Пов-ть z=f(x,y). Геом смысл ∫∫ для ф-и f(x,y) по обл-ти D заключается в следующем: если ф-я f(x,y) неотриц в обл-ти D, то ∫∫ по обл-ти D от f(x,y) = объему цилиндрич тела, ограниченного: сверху пов-ю z=f(x,y), снизу областью D, в к-ю проэктируется эта пов-ть в пл-ти хоу, с боков – цилиндрич пов-ю с образующими || оси Оz. =V_{ЦИЛИНДРИЧ ТЕЛА}

Св-ва ∫∫

1) =S_D, f(x,y)=1, (x,y) D

2) f₁(x,y), f₂(x,y) - интегрир в D, то их алг сумма интегрир в D [f₁(x,y)± f₂(x,y)] ∫∫[f₁(x,y)± f₂(x,y)]dxdy=∫∫f₁(x,y)dxdy± ∫∫f₂(x,y)dxdy При условии, что они интегрируемы

3) λ R, f(x,y) интегрир на D, то λf(x,y) тоже инт-ма на D. Справедливо ∫∫λf(x,y)dxdy=λ∫∫f(x,y)dxdy

4) Если ф-я f(x,y) интегрируема в D и некоторой произвольной кривой обл-ти D разбивается на 2 обл-ти D₁ и D₂, в каждой из к-х эта ф-я интегрируема, то f(x,y)dxdy= f(x,y)dxdy± f(x,y)dxdy. При док-ве эту кривую включают в разбиение.

5) Если f(x,y), g(x,y) интегрир в обл-ти D, причем f(x,y)≤g(x,y) в D (x,y) D, то f(x,y)dxdy≤ g(x,y)dxdy

6) Если f(x,y) интегрируема в D, то | f(x,y)dxdy| ≤ |f(x,y)|dxdy. -|f(x,y)| ≤f(x,y)≤|f(x,y)|.

7) Теорема о среднем: Если ф-я f(x,y) непр в D, то найдется единств т (ξ,η) такая что f(x,y) интегрируема в D. !( ξ,η) D: f(x,y)dxdy=f(ξ,η)S_D Док-во: Т.к. ф-я непр в D, тона достигает наим, наиб знач m-наим, М- наиб знач f(x,y) в D. m ≤f(x,y) ≤M, (x,y) D. По 5 св-ву: mdxdy ≤ f(x,y)dxdy ≤ Mdxdy, По 3 св-ву: m, M- константы → m dxdy ≤ f(x,y)dxdy ≤M f(x,y). По св-ву: mS_D ≤ f(x,y)dxdy ≤MS_D. m ≤ f(x,y)dxdy / S_D ≤M.

Согласно т о промежут знач ф-и 2х найдется: (x,y) (D): f(x,y)dxdy / S_D=f(x,y). Умножим на S_D обе части: f(x,y)dxdy=f(x,y)S_D Ч.т.д.

Вычисление ∫∫ в Декарт сист корд:

☼ Обл-ть D- правильная в направлении оси oy (ординат), если любая прямая || oy и проходящая ч\з внутр т обл-ти D пересекает границу этой обл-ти в 2х точках – т. входа обл-ти и обл-ти выхода из обл-ти.

☼ Обл-ть D- правильная в направлении оси oх (абсцисс), если любая прямая || oх и проходящая ч\з внутр т обл-ти D пересекает границу этой обл-ти в 2х точках – т. входа обл-ти и обл-ти выхода из обл-ти.

Об-ть прав в оси ох и оу – наз-ся правильной. Зам-е: Если указ прямая в определении (|| оси), проходит через границу обл-ти, то с границей имеет 1 общ т. Или несколько (беск мн-во) точек.

Двухкратным (повторным) интегралом наз-ся инт вида:

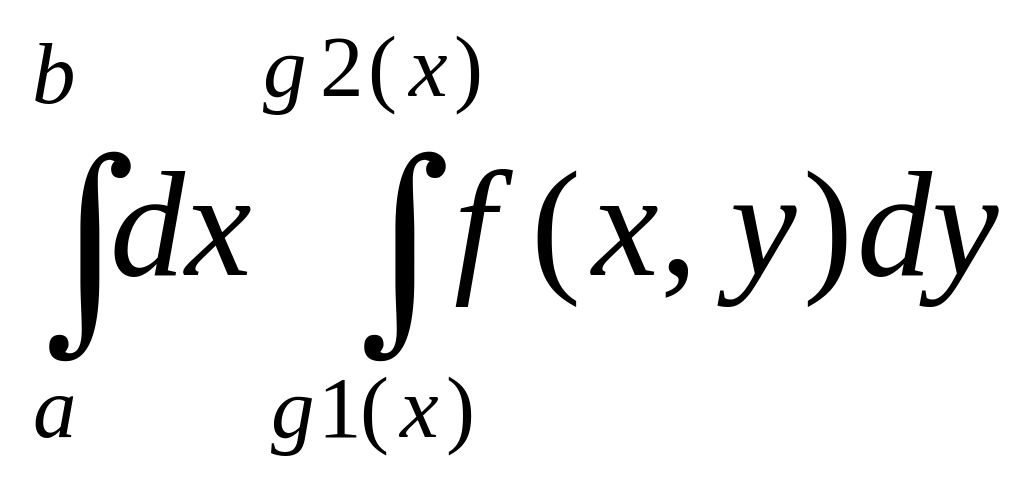, если обл-ть Dправильная в направлении оу (оси ординат) или интеграл вида: , где обл-ть D правильная в напр оси абсцисс (ох). Теорема: Если ф-я f(x,y) непр обл-ти D, к-я правильная в напр оси ординат (оу), то ∫∫ вычисляется по след ф-ле. f(x,y)dxdy= . Если f(x,y) непр в обл D, к-я правильн в направлении оси абсц (ох), то f(x,y)dxdy=