Регрессия

Корреляционный анализ служит той же цели, что и дисперсионный анализ, добавляя к установлению связи, оценку степени этой связи. Следует научиться выражать стохастическую связь через функциональные соотношения. Пусть наблюдаются 2 случайные величины х и y. При сопоставлении этих величин, все ошибки можно отнести к одной из них (у), а величину х при этом считать не случайной величиной. В этом случае ошибка будет складываться из собственной ошибки и ошибки сопоставления.

Рассмотрим случайную величину Y от неслучайного параметра Х. При каждом значении Х величина Y будет обладать каким-то законом распределения F(Y)=F(Y,X).Если найден закон распределения Х и Y, то тем самым полностью определена стохастическая зависимость.

Пусть при каждом значении Х величина Y имеет нормальное распределение. А нормальное распределение полностью определяется генеральным средним а и генеральной дисперсией σ². Таким образом, связь между величинами Х и Y будет полностью определена, если известны зависимости:

{ aY=a(x), σ²Y=σ²(x).

Зависимость σ²Y=σ²(x) называется скедостической. Она используется редко. На практике чаще используют сводную дисперсию, характеризующую рассеяние Y при всех значениях Х.

Зависимость среднего от Х наз. Регрессией. регрессия даёт истинную зависимость СВ Y от Х.

На практике находится приближенная регрессия. Задача ставится таким образом: по выборке, образованной из пар (x1,Y1),(X2,Y2),……(Xn,Yn) необходимо найти уравнение приближенной регрессии и оценить дополнительную при этом ошибку. Уравнение, приближенное регрессией, существенно зависит от выбираемого принципа приближения. Т.к. Yi не совпадает с точным значением Yi=а=a(Xi)

Y=a=a(X), то уравнение регрессии не обязано давать на всех парах чисел (XiYi) точное равенство. График уравнения регрессии не обязан проходить через все экспериментальные точки. В качестве принципа приближения обычно используют принцип наименьших квадратов. Для этого принципа мерой рассеяния всех Yi=f(X) вокруг уравнения приближенной регрессией имеет величина:

n-число точек.

l-число связей, накладываемых на выборку уравнением регрессии.

Предположим, получено 2 уравнения регрессии:

Y=f₁(x), D₁

Y=f₂(x), D₂

Из этих двух уравнений выбирается то, для которого D меньше.

Пусть задан некоторый класс функций, среди которых находится уравнение регрессии. Все эти функции накладывают на выборку одинаковое число связей.

Тогда для этого класса функции число l будет иметь фиксированное значение и для выборок уравнения регрессии и определения меры рассеяния можно вычислить такую величину:

Класс функций используемых для нахождения уравнений регрессии, используется несколько произвольных коэффициентов. Эти коэффициенты вычисляются по заданной выборке, поэтому каждый из них представляет собой связь, накладываемую на выборку.

Например, уравнение регрессии можно выбирать из полиномов в степени m

y=a₀+a₁*x¹+…+a_m*x^m

Число коэффициентов m+1

Все эти коэффициенты вычисляются по результатам выборки: l= m+1.

Для получения уравнения приближенной регрессии, необходимо найти все неопределенные коэффициенты (a_i). Которые минимизируют величину S. условием экстремума:

Число уравнений = числу неизвестных аi.

Пример:

Пусть уравнение регрессии получают из класса квадратичных функций:

y=a₀+a₁*x¹+a₂*x²

В результате система уравнений для нахождения коэффициентов а0, а1, а2 принимает вид:

Получили систему 3-х уравнений с тремя неизвестными.

Чтобы оценить степень приближенности найденного уравнения, необходимо найти оценки для всех коэффициентов а₀, а₁, а₂.

Уравнение регрессии можно получать путём последовательного уточнения.

Допустим, получено уравнение регрессии (прибл.) Y=f(x) и предполагается заменить уточненным уравнением: Y=f(x)+φ(x).

Поправка φ(x) может отвергаться по двум причинам:

1) у неё может быть большое число связей, что может привести к увеличению дисперсии D.

2) она может оказаться, мала в сравнении с ошибкой наблюдения.

Сначала проверим, нуждается ли уравнение регрессии f(x) в уточнении. Допустим, для уравнения Y=f(x) величина дисперсии D, а случайная ошибка определяется выборочной дисперсией S². Проверяется выполнение такого соотношения:

- надо уточнять

- не надо уточнять.

Допустим, выполняется условие , значит уравнение регрессии нуждается в уточнении: D1(l1) и D2(l2).

Мальцев

И берется соотношение

Линейная регрессия

Линейная регрессия наиболее часто используется на практике. Нелинейная регрессия во многих случаях получается путем её сведения к линейной

Линейную регрессию запишем в таком виде: y=ax+b

Система для нахождения и принимает вид

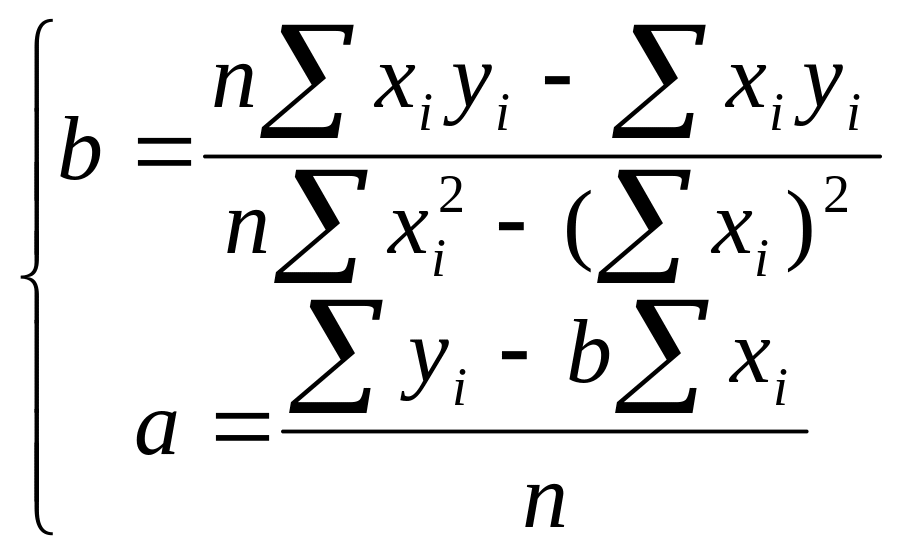
Можно убедиться, что линия приближенной регрессии проходит через среднюю точку , поэтому для нахождения уравнения регрессии достаточно определить коэффициент b .

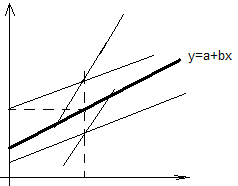
Так как находится по результатам выборки, то при этом допускается погрешность. Истинное значение параметра находится в пределах :