
Действия над комплексными числами в алгебраической форме.
Комплексным числом называется упорядоченная пара действительных чисел z=(a,b) где a и b принадлежат R. R-действительное число.
Суммой двух упорядоченных пар α= (а, b) и β = (с, d) назовем упорядоченную пару γ = (a+c, b+d):
(a, b) + (c, d) = (a + c, b + d), (1)
произведением указанных пар — упорядоченную пару δ = (ас – bd, ad + bc):
(a, b)(c, d) = (ac – bd, ad + bc). (2)
С - множество всех комплексных чисел.
Z=(a,b) a= ReZ – действительная часть b=ImZ – мнимая часть.
Разностью α — β двух упорядоченных пар α = (a, b) и β = (с, d) назовем такую упорядоченную пару (х, y), для которой (с, d) + (x, y) = (a, b). Принимая во внимание равенство (1), получаем с + х = a, d + y = b, откуда x = а – c, y = b – d. Разностью α — β упорядоченных пар α = (а, b) и β = (с, d) является упорядоченная пара (а – c, b – d):
(a, b) – (c, d) = (a – c, b – d). (3)
Нулем служит пара 0 = (0, 0). Упорядоченной парой, противоположной для упорядоченной пары α = (а, b) будет, пара - α = ( -а, -b), так как α + (-α) = (а, b) + (-а, -b) = (0,0) = 0.
Частным от деления упорядоченной пары α = (а, b) на упорядоченную пару β = (с, d), где β 0 или с + d 0 (т. е. хотя бы одно из чисел с, d отлично от нуля) должна быть упорядоченная пара (x, y) такая, что (с, d) (x, y) = (а, b). Отсюда на основании равенства (2) получаем cx – dy = a, cy – dx = b. Из этой системы уравнений находим x и y:x = , y = .
Итак, если β 0, то частное α/β двух упорядоченных пар α = (а, b), β = (с, d) существует и определяется формулой: |
= . (4)Положив в этой формуле β = α (т. е. c = a, d = b), найдем, что единицей при умножении упорядоченных пар служит упорядоченная пара (1, 0). Полагая α = 1 = (1, 0), из формулы (4) получаем, что при β 0 упорядоченной парой, обратной для β, будет упорядоченная пара.
Если
комплексное число ![]() ,
то число
,
то число ![]() называется сопряжённым (или
комплексно сопряжённым) к
называется сопряжённым (или
комплексно сопряжённым) к ![]() (обозначается
также
(обозначается
также ![]() ).
На комплексной плоскости сопряжённые
числа получаются зеркальным отражением
друг друга относительно вещественной
оси. Модуль сопряжённого числа такой
же, как у исходного, а их аргументы
отличаются знаком.
).
На комплексной плоскости сопряжённые
числа получаются зеркальным отражением
друг друга относительно вещественной
оси. Модуль сопряжённого числа такой
же, как у исходного, а их аргументы
отличаются знаком.
Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.
 (сопряжённое
к сопряжённому есть исходное).
(сопряжённое
к сопряжённому есть исходное).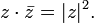
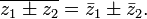
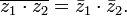

2 Действия над комплексными числами в тригонометрической форме.

r = sqrt(a2+ b2) cosf = a/r a = r*cosf sinf = b/r b = r*sinf
a + bi = r*(cosf + isinf)
Число r - модуль комплексного числа. f - аргумент комплексного числа (argZ, Z = a + bi) Аргумент Z определяется с точностью до слагаемого равного 2*pi и может быть как положительным так и отрицательным. Обычно главное значение argZ выбирается в промежутке [0, 2*pi]. Запись: Z = a + bi - алгебраическая форма. Запись: Z = r*(cosf + isinf) - тригонаметрическая форма.
Действия:
Z1 = r1(cosf1+ isinf1) Z2 = r2(cosf2+ isinf2) Z1*Z2 = r1(cosf1 + isinf1) * r2(cosf2+ isinf2) = r1*r2[(cosf1*cosf2- sinf1*sinf2) + (cosf1*sinf2+ sinf1*cosf2)i] = = r1*r2[cos(f1+ f2) + sin(f1+ f2)i] Z1/Z2 = [r1(cosf1+ isinf1)] / [r2(cosf2+ isinf2)] = (r1/r2) * [(cosf1+ isinf1) * (cosf2- isinf2) / (cos2f2+ isin2f2)] = = (r1/r2) * [cos(f1- f2) + sin(f1- f2)i] Zn = rn(cosfn + isinfn) Z1/n = r1/n[cos((f + 2*pi*k)/n) + isin((f + 2*pi*k)/n)], k = 0, 1, ..., n-1
Основная теорема алгебры.
Основна́я теоре́ма а́лгебры утверждает, что
Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.
Немедленным
следствием из теоремы является то, что
любой многочлен степени ![]() над
полем комплексных чисел имеет в нём
ровно
корней,
с учётом кратности корней.
над
полем комплексных чисел имеет в нём
ровно
корней,
с учётом кратности корней.
Доказательство.
У
многочлена ![]() есть
корень
есть
корень ![]() ,
значит, по теореме
Безу,
он представим в виде
,
значит, по теореме
Безу,
он представим в виде ![]() ,
где
,
где ![]() —
другой многочлен. Применим теорему
к
и
будем применять её таким же образом до
тех пор, пока на месте
не
окажется линейный множитель.
—
другой многочлен. Применим теорему
к
и
будем применять её таким же образом до
тех пор, пока на месте
не
окажется линейный множитель.
Доказательство.
Представим
полином ![]() в
виде суммы
в
виде суммы ![]() ,
где
,
где ![]() ,
, ![]() .
Составим соотношение
.
Составим соотношение ![]() .
Легко видеть, что для любых
коэффициентов
.
Легко видеть, что для любых
коэффициентов ![]() всегда
найдется такое значение
всегда
найдется такое значение ![]() ,
что для всех значений
,
что для всех значений ![]() имеет
место неравенство
имеет
место неравенство 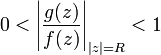 .
В силу теоремы
Руше следует,
что полное число нулей функции
.
В силу теоремы
Руше следует,
что полное число нулей функции ![]() в
круге
в
круге ![]() равно
числу нулей в этом круге функции
.
Но функция
на
всей комплексной плоскости имеет один
единственный n-кратный корень
равно
числу нулей в этом круге функции
.
Но функция
на
всей комплексной плоскости имеет один
единственный n-кратный корень ![]() .
Отсюда, в силу произвольности
.
Отсюда, в силу произвольности ![]() и
следует утверждение теоремы.
и
следует утверждение теоремы.
Самое простое доказательство этой теоремы даётся методами комплексного анализа. Используется тот факт, что функция, аналитическая на всей комплексной плоскости и не имеющая особенностей на бесконечности, есть константа. Посему, функция 1/p, где p — многочлен, должна иметь хоть один полюс на комплексной плоскости, а, соответственно, многочлен имеет хоть один корень.
Первообразная. Неопределенный интеграл.
Определение
первообразной.
Первообразной
функции f(x) на
промежутке (a;
b) называется
такая функция F(x),
что выполняется равенство ![]() для
любого х из
заданного промежутка.
Если принять
во внимание тот факт, что производная
от константы С равна
нулю, то справедливо равенство
для
любого х из
заданного промежутка.
Если принять
во внимание тот факт, что производная
от константы С равна
нулю, то справедливо равенство ![]() .
Таким образом, функция f(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение
неопределенного интеграла.
Все
множество первообразных функции f(x) называется
неопределенным интегралом этой функции
и обозначается
.
Таким образом, функция f(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение
неопределенного интеграла.
Все
множество первообразных функции f(x) называется
неопределенным интегралом этой функции
и обозначается ![]() .
Выражение
.
Выражение ![]() называют подынтегральным
выражением,
а f(x) – подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие
нахождения неизвестной функции по
заданному ее дифференциалу называется
неопределенным интегрированием,
потому что результатом интегрирования
является не одна функцияF(x),
а множество ее первообразных F(x)+C.
называют подынтегральным
выражением,
а f(x) – подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие
нахождения неизвестной функции по
заданному ее дифференциалу называется
неопределенным интегрированием,
потому что результатом интегрирования
является не одна функцияF(x),
а множество ее первообразных F(x)+C.
Свойства неопределенного интеграла.
Свойство
1. Производная
от неопределённого интеграла равна
подынтегральной функции, то есть если
![]() , то
, то
![]()
Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению
![]()
Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы
![]()
Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов
![]()
Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов
![]()
Свойство 6. Постоянный множитель можно выносить за знак интеграла
![]()
Свойство 7. Если
то
![]()
Таблица интегралов.
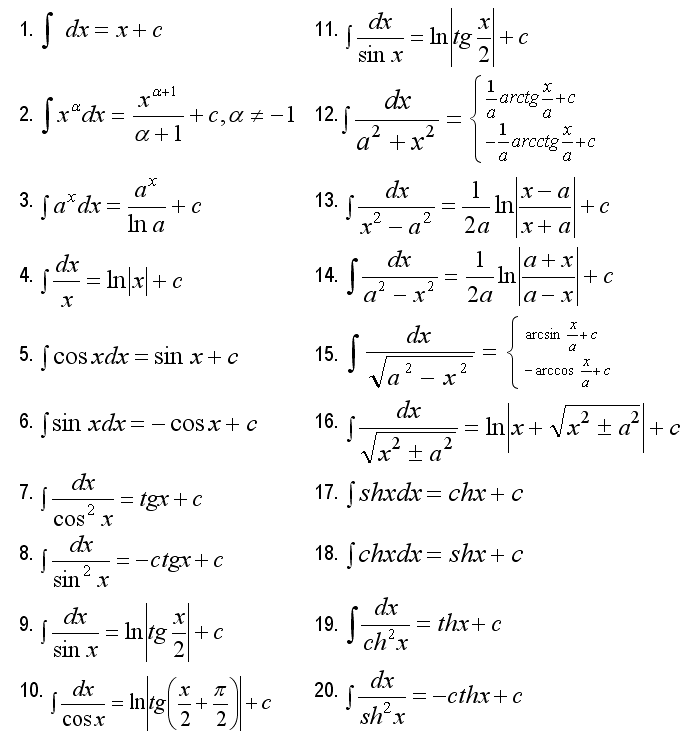
Замена переменной в неопределенном интеграле.
Простейшие дроби и их интегрирование.
Разложение рациональных дробей на простейшие и их интегрирование.
Представление рациональной дроби в виде суммы целой части и простейших дробей.
11Интегрирование рациональных функций.
12Интегрирование некоторых иррациональных функций.
13Интегрирование некоторых трансцендентных функций.
14Определенный интеграл: определение, геометрический смысл и свойства.
Пусть
определена
на ![]() .
Разобьём
на
части с несколькими произвольными
точками
.
Разобьём
на
части с несколькими произвольными
точками ![]() Тогда
говорят, что произведено
разбиение
Тогда
говорят, что произведено
разбиение ![]() отрезка
отрезка ![]() Далее
выберем произв. точку
Далее
выберем произв. точку ![]() ,
, ![]() ,
,
Определённым
интегралом от функции
на
отрезке
называется
предел интегральных сумм при стремлении
ранга разбиения к нулю ![]() ,
если он существует независимо от
разбиения
и
выбора точек
,
если он существует независимо от
разбиения
и
выбора точек ![]() ,
т.е.
,
т.е.
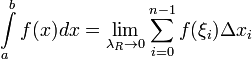
Если существует указанный предел, то функция называется интегрируемой на по Риману.
Геометрический смысл
![]()
Определённый интеграл как площадь фигуры
Определённый
интеграл 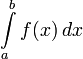 численно
равен площади фигуры, ограниченной осью
абсцисс, прямыми
численно
равен площади фигуры, ограниченной осью
абсцисс, прямыми ![]() и
и ![]() и
графиком функции
.
и
графиком функции
.
Свойства
Если функция интегрируема по Риману на , то она ограничена на нем.
Теорема о среднем.
Теорема о среднем в определённом интеграле
Пусть
функция f(x) непрерывна на
[a, b], тогда 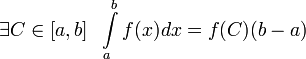 .
.
Доказательство
1.
По свойству функции, непрерывной на
отрезке, ![]() ,
такие что
,
такие что ![]() .
.
2.
По свойству определенного
интеграла  ,
следовательно
,
следовательно 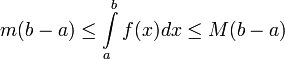 ,
, 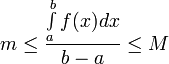 .
Обозначим дробь как
.
Обозначим дробь как ![]() .
.
3.
Так как непрерывная функция принимает
все свои промежуточные значения, а ![]() ,
то
,
то ![]() ,
такая что
,
такая что 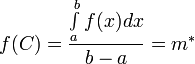 .
.
Вычисление определенного интеграла. Формула Ньютона – Лейбница.
Формула
Ньютона-Лейбница.
Пусть
функция y
= f(x) непрерывна
на отрезке [a;
b] и F(x) -
одна из первообразных функции на этом
отрезке, тогда справедливо равенство 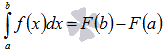 .
Эту
формулу называют основной
формулой интегрального исчисления.
.
Эту
формулу называют основной
формулой интегрального исчисления.
Замена переменной в определенном интеграле.
ТЕОРЕМА.
Пусть функция φ(t) имеет непрерывную
производную на отрезке [α,β], а=φ(α), в=φ(β)
и функция f(х) непрерывна в каждой точке
х вида х=φ(t), где t![]() [α,β].
[α,β].
Тогда справедливо следующее равенство:
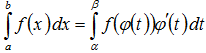
Эта формула носит название формулы замены переменной в определенном интеграле.
Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).
Интегрирование по частям в определенном интеграле.
Несобственные интегралы I и II рода и признаки их сходимости.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
Предел a или b (или оба предела) являются бесконечными;
Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
Несобственные интегралы I рода
Пусть
определена
и непрерывна на множестве от ![]() и
и 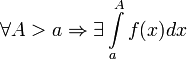 .
Тогда:
.
Тогда:
Если
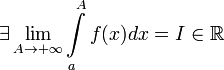 ,
то используется обозначение
,
то используется обозначение  и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
называется
сходящимся.Если не существует конечного
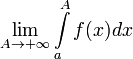 (
(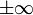 или
или  ),
то интеграл
),
то интеграл 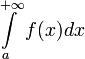 называется
расходящимся к
называется
расходящимся к  ,
или просто расходящимся.
,
или просто расходящимся.
Пусть
определена
и непрерывна на множестве от ![]() и
и 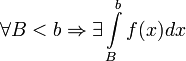 .
Тогда:
.
Тогда:
Если
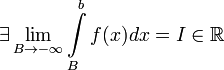 ,
то используется обозначение
,
то используется обозначение  и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
называется
сходящимся.Если не существует конечного
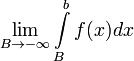 (
или
),
то интеграл
(
или
),
то интеграл 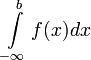 называется
расходящимся к
,
или просто расходящимся.
называется
расходящимся к
,
или просто расходящимся.
Если функция определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
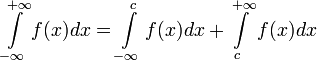 ,
где с — произвольное число.
,
где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.
Несобственные интегралы II рода
Пусть
определена
на ![]() ,
терпит бесконечный разрыв в точке x=a
и
,
терпит бесконечный разрыв в точке x=a
и 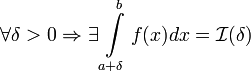 .
Тогда:
.
Тогда:
Если
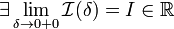 ,
то используется обозначение
,
то используется обозначение 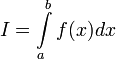 и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.Если
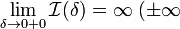 или
или 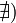 ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а  называется
расходящимся к
,
или просто расходящимся.
называется
расходящимся к
,
или просто расходящимся.
Пусть
определена
на ![]() ,
терпит бесконечный разрыв при x=b и
,
терпит бесконечный разрыв при x=b и 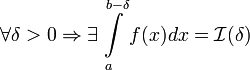 .
Тогда:
.
Тогда:
Если
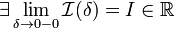 ,
то используется обозначение
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
,
то используется обозначение
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.Если
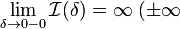 или
,
то обозначение сохраняется, а
называется
расходящимся к
,
или просто расходящимся.
или
,
то обозначение сохраняется, а
называется
расходящимся к
,
или просто расходящимся.
Если
функция
терпит
разрыв во внутренней точке ![]() отрезка
,
то несобственный интеграл второго рода
определяется формулой:
отрезка
,
то несобственный интеграл второго рода
определяется формулой:
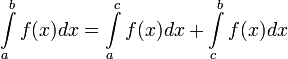
Геометрический смысл несобственных интегралов II рода
Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции
Отдельный случай
Пусть
функция
определена
на всей числовой оси и имеет разрыв в
точках ![]() .
.
Тогда
можно найти несобственный интеграл 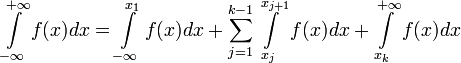
Абсолютная сходимость
Интеграл 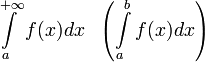 называется абсолютно
сходящимся,
если
называется абсолютно
сходящимся,
если 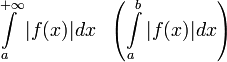 сходится.
Если
интеграл сходится абсолютно, то он
сходится.
сходится.
Если
интеграл сходится абсолютно, то он
сходится.
Условная сходимость
Интеграл 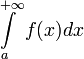 называется условно
сходящимся,
если
сходится,
а
называется условно
сходящимся,
если
сходится,
а 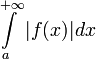 расходится.
расходится.
Геометрические приложения определенных интегралов.
Если
на отрезке ![]() функция
функция ![]() , то площадь
криволинейной трапеции,
ограниченной кривой
, то площадь
криволинейной трапеции,
ограниченной кривой ![]() , осью
, осью ![]() и прямыми
и прямыми ![]() (рис. 9), равна
(рис. 9), равна
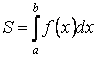
Если ![]() на отрезке
, то площадь соответствующей
криволинейной трапеции
на отрезке
, то площадь соответствующей
криволинейной трапеции
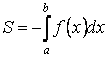
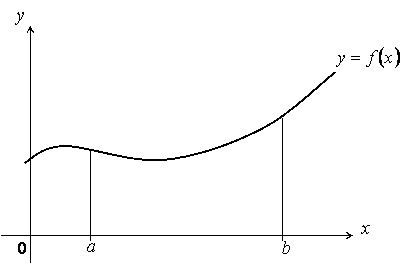 Рисунок
9.
Рисунок
9.
В общем случае, когда функция
![]() меняет знак на отрезке
(рис. 10), площадь, ограниченная кривой
, осью
и прямыми
может быть найдена как сумма площадей
фигур, лежащих выше и ниже оси
. Иначе
меняет знак на отрезке
(рис. 10), площадь, ограниченная кривой
, осью
и прямыми
может быть найдена как сумма площадей
фигур, лежащих выше и ниже оси
. Иначе

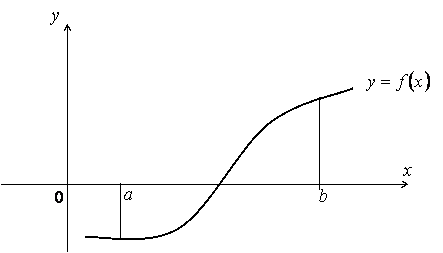 Рисунок
10.
Рисунок
10.
Длина дуги кривой , ограниченной точками с абсциссами , вычисляется по формуле

Рассмотрим тело, образованное вращением вокруг оси криволинейной трапеции, ограниченной кривой , осью и прямыми . Объём тела вращения

Пусть кривая задана уравнениями в параметрической форме
![]() ,
,
где
![]() и
и ![]() . Площадь криволинейной трапеции в
этом случае равна
. Площадь криволинейной трапеции в
этом случае равна

а длина дуги

Пусть кривая задана уравнением в полярной системе координат
![]() ,
,
где
![]() - непрерывная функция, определённая
при
- непрерывная функция, определённая
при ![]() (рис. 11). Площадь сектора, ограниченного
заданной кривой и лучами
(рис. 11). Площадь сектора, ограниченного
заданной кривой и лучами ![]() ,
, ![]() , равна
, равна

 Рисунок
11.
Рисунок
11.
Длина дуги кривой, определённой в полярной системе координат уравнением , вычисляется по формуле
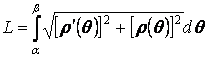
Вычисление плоских фигур.
Функции многих переменных: определение. Область определения и область значения
Обозначим
через D некоторое
множество точек в п-мерном
пространстве.
Если
задан закон f ,
в силу которого каждой
точке М(х ![]() ;...;х
;...;х ![]() )
) ![]() D ставится
в соответствие число и,
то говорят, что на множестве D определена
функция и= f(х
;...;х
).
Множество
точек М(х
;...;х
),
для которых функция и= f(х
;...;х
)
определена, называют областью
определения этой
функции и обозначают D(f).
Функции
многих переменных можно обозначать
одним символом и=f(М),
указывая размерность пространства,
которому принадлежит точка М.
Функции
двух переменных можно изобразить
графически в виде некоторой
поверхности.
Графиком
функции двух переменных z=f(х;у)
в прямоугольной системе координат Оху называется
геометрическое место точек в трехмерном
пространстве, координаты которых (х;у;z)
удовлетворяют уравнению z=f(х;у).
D ставится
в соответствие число и,
то говорят, что на множестве D определена
функция и= f(х
;...;х
).
Множество
точек М(х
;...;х
),
для которых функция и= f(х
;...;х
)
определена, называют областью
определения этой
функции и обозначают D(f).
Функции
многих переменных можно обозначать
одним символом и=f(М),
указывая размерность пространства,
которому принадлежит точка М.
Функции
двух переменных можно изобразить
графически в виде некоторой
поверхности.
Графиком
функции двух переменных z=f(х;у)
в прямоугольной системе координат Оху называется
геометрическое место точек в трехмерном
пространстве, координаты которых (х;у;z)
удовлетворяют уравнению z=f(х;у).
Предел функции в точке, повторные пределы. Непрерывность функции в точке
Пусть функция f(x) определена в некоторой проколотой окрестности точки x0 .
Число A называется пределом функции f(x) при x → x0 (или в точке x0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < |x − x0| < δ, справедливо неравенство |f(x) − A| < ε, т.е.
lim |
x → x0 |
f(x) = A ε > 0 δ > 0 : 0 < |x − x0| < δ |f(x) − A| < ε.
Используем понятие окрестности и учтем, что
0 < |x − x0| < δ x
· |
O |
δ (x0 ) и |f(x) − A| < ε f(x) Oε (A).
(Точка над символом окрестности указывает, что это проколотая окрестность.)
Теперь определение предела функции в точке можно представить в виде
|
f(x) = A ε > 0 δ > 0 : x
δ (x0 ) f(x) Oε (A). |
|
Еше проще:
|
f(x) = A O (A)
(x0) : x
(x0) f(x) O (A). |
|
Геометрический смысл того, что x
(x0) f(x) O (A) поясняет рис.1

На этом рисунке проколотая окрестность
(x0) точки x0 изображена красным отрезком на оси OX из которого исключена точка x0. Окрестность O (A) точки Aизображена розовым отрезком на оси OY. Очевидно, что образ окрестности
(x0) при отображении y = f(x) содержится в O (A).
Для
функции нескольких переменных ![]() можно
определить понятие предела по одной из
переменных
можно
определить понятие предела по одной из
переменных ![]() при
фиксированных значениях остальных
переменных. В связи с этим возникает
понятие повторного
предела.
при
фиксированных значениях остальных
переменных. В связи с этим возникает
понятие повторного
предела.
Определение
Рассмотрим
функцию двух переменных ![]() ,
определенную в некоторой выколотой
окрестности точки
,
определенную в некоторой выколотой
окрестности точки ![]() .
Выберем и зафиксируем переменную
.
Выберем и зафиксируем переменную ![]() .
Получим функцию как бы одной переменной.
Рассмотрим предел:
.
Получим функцию как бы одной переменной.
Рассмотрим предел:
![]()
Будем
считать, что ![]() существует.
Теперь снимем фиксацию с переменной
и
рассмотрим следующий предел:
существует.
Теперь снимем фиксацию с переменной
и
рассмотрим следующий предел:
![]()
Если
этот предел существует, то говорят,
что ![]() есть
повторный предел функции
в
точке
.
есть
повторный предел функции
в
точке
.
![]()
Аналогично
мы можем фиксировать сначала переменную ![]() .
В этом случае мы также получим повторный
предел, но, вообще говоря, другой:
.
В этом случае мы также получим повторный
предел, но, вообще говоря, другой:
![]()
Это определение можно распространить и на функции нескольких переменных .
Функция f(x) называется непрерывной в точке x0, если существует limx → x0 f(x) , равный значению функции f(x) в этой точке:
|
f(x) = f(x0), |
Функция y = f(x) непрерывна в точке х0 тогда и только тогда, когда
|
Δy = 0. |
|
Функция f(x) называется непрерывной справа в точке x0, если существует односторонний предел
|
f(x) = f(x0). |
|
Пусть функция f(x) определена в полуинтервале (x0 − δ, x0].
Функция f(x) называется непрерывной слева в точке x0, если существует односторонний предел
|
f(x) = f(x0). |
Частные производные. Полный дифференциал.
