
Частные производные высших порядков
Пусть
задана функция f(x,
y).
Тогда каждая из ее частных
производных(если
они, конечно, существуют) ![]() и
и ![]() ,
которые называются также частными
производными первого порядка,
снова являются функцией независимых
переменных x,
y и
может, следовательно также иметь частные
производные. Частная производная
,
которые называются также частными
производными первого порядка,
снова являются функцией независимых
переменных x,
y и
может, следовательно также иметь частные
производные. Частная производная  обозначается
через
обозначается
через ![]() или
или ![]() ,
а
,
а  через
через ![]() или
или ![]() .
Таким образом,
.
Таким образом,
 ,
, 
и, аналогично,
 ,
,  .
.
Производные ![]() и
и ![]() называются частными
производными второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка:
называются частными
производными второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка: ![]() ,
, ![]() ,
, ![]() и т. д.
и т. д.
Экстремум функции многих переменных (при п=2) условный экстремум.
Определение двойного интеграла и его свойства.
В
прямоугольных координатах:  ,
где
,
где ![]() —
элемент площади в прямоугольных
координатах.
—
элемент площади в прямоугольных
координатах.
Геометрический смысл двойного интеграла
Пусть
функция
принимает
в области ![]() только
положительные значения. Тогда двойной
интеграл
только
положительные значения. Тогда двойной
интеграл  численно
равен объему
численно
равен объему ![]() вертикального
цилиндрического тела, построенного на
основании
и
ограниченного сверху соответствующим
куском поверхности
вертикального
цилиндрического тела, построенного на
основании
и
ограниченного сверху соответствующим
куском поверхности ![]() .
.

Геометрический смысл двойного интеграла
Выражение двойного интеграла через полярные координаты

Переход из прямоугольных координат в полярные.

Переход из прямоугольных координат в полярные.
В некоторых случаях двойной интеграл проще считать не в прямоугольных, а в полярных координатах, так как при этом может произойти существенное упрощение вида области интегрирования и всего процесса интегрирования в целом.
Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:

Модуль
якобиана отображения равен ![]() .
Таким образом получаем, что
.
Таким образом получаем, что
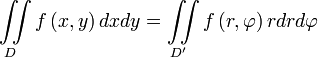 .
.
Здесь ![]() является
элементом площади в полярных координатах.
является
элементом площади в полярных координатах.
СВОЙСТВО ДВОЙНЫХ ИТЕГРАЛОВ
1.
Если функция f(x, y) интегрируема в D, то
kf(x, y) тоже интегрируема в этой области,
причем ![]()
Если в области D интегрируемы функции f(x, y) и g(x, y), то в этой области интегрируемы и функции f(x, y) ± g(x, y), и при этом
![]()
3. Если для интегрируемых в области D функций f(x, y) и g(x, y) выполняется неравенство f(x, y) ≤ g(x, y) , то
![]()
Сведение двойного интеграла к повторному. Изменение порядка интегрирования.
Сведение двойного интеграла к повторному
Область D называется правильной вдоль оси OY, если прямая, параллельная оси OY, пересекает границу области D в двух точках.

Пусть область правильная вдоль оси OY, нижние точки границы лежат на линии с уравнением у = φ (х), верхние — на линии с уравнением у = ψ(х). Тогда двойной интеграл можно привести к повторному

Вычисление двойного интеграла в полярной системе координат.
Вычисление двойного интеграла в полярных координатах:
Для вычисления двойного интеграла в полярных координатах применяют тоже правило сведения его к двукратному интегралу.
Если
область ![]() ограничена
лучами
ограничена
лучами ![]() и
и ![]() ,
где
,
где ![]() и
кривыми
и
кривыми ![]() и
и ![]() ,
где
,
где ![]() ,
т.е. область
правильная,
то:
,
т.е. область
правильная,
то:

