Модели и методы принятия решений

Задача 1

Решить графическим методом

Max φ(X)=x1 + x2

2 ∙ x1 + 4 ∙ x2 ≤ 16

-4 ∙ x1 + 2 ∙ x2 ≤ 8

x1 + 3 ∙ x2 ≥ 9

x ≥ 0

На основе исходных данных строим многоугольник решений:

Многоугольником решений для данной задачи является треугольник АВС увеличивая значения целевой функции видим, что граничной точкой, в которой целевая функция достигает максимальное значение является точка С. Решаем систему уравнений прямых пересекающихся в данной точке. И находим ее координаты :

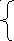
2 ∙ x1 + 4 ∙ x2 = 16

x1 + 3 ∙x2 = 9

Решение системы :

x1=9-3 ∙ x2 →

-6 ∙ x2 + 4 ∙ x2 = 16-18 →

2 ∙ x2=2 →

x2=1 →

x1=9-3=6 →

С(6;1)

Подставив полученные значения в целевую функцию получим максимальное значение функции в данной точке :

Max φ(X)=7

Задача 2

Решить методом Лагранжа. Решение проиллюстрировать графически.

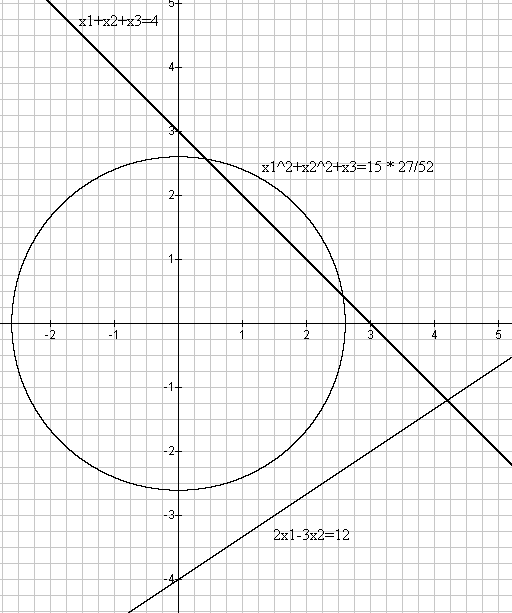
extr φ(X) = x1² + x2² + x3

x1 + x2 + x3 = 4

2 ∙ x1 - 3 ∙ x2 = 12

Строим функцию Лагранжа

L(X,λ) = x1² + x2² + x3+ λ1 ∙ (x1 + x2 + x3-4)+ λ2 ∙ (2 ∙ x1 - 3 ∙ x2-12)

dL(X,λ)/dx1 = 2 ∙ x1 - λ1 - 2 ∙ λ2 = 0

dL(X,λ)/dx2 = 2 ∙ x2 - λ1 + 3 ∙ λ2 = 0

dL(X,λ)/ x3 = 1 - λ1 = 0

dL(X,λ)/ λ1 = x1 + x2 + x3-4 = 0

dL(X,λ)/ λ2 = 2 ∙ x1 - 3 ∙ x2-12 = 0

Решение системы :

λ1 = 1 →

x1 = λ2 + 0,5 ; x2 = 0,5-1,5 ∙ λ2 →

2 ∙ (λ2 + 0,5) - 3 ∙ (0,5-1,5 ∙ λ2) = 12 ; 6,5 ∙ λ2 = 12,5 ; λ2 = 1 ∙ 12/13 →

x1 = 2 ∙ 11/26 ; x2 = -2 ∙ 2/13 →

x3 = 4 - 2 ∙ 11/26 + 2 ∙ 2/13 = 3 ∙ 25/26

Подставив полученные значения в целевую функцию получим максимальное значение функции в данной точке :

Max φ(X)=15 ∙ 27/52

Решение проиллюстрируем графически :

Задача 3

Решить методом Лагранжа или на основе условий Куна-Таккера. Решение проиллюстрировать графически.

extr φ(X) = x2-x1² + 6 ∙ x1

3 ∙ x1 + 2 ∙ x2 ≤ 24

x1+2 ∙ x2 ≤15

Строим функцию Лагранжа

L(X,λ) = x2-x1² + 6 ∙ x1+ λ1 ∙ (3 ∙ x1 + 2 ∙ x2 -24)+ λ2 ∙ (x1+2 ∙ x2 -15)

dL(X,λ)/dx1 = 2 ∙ x1 + 3 ∙ λ1 + λ2 - 6 ≥ 0

dL(X,λ)/dx2 = 2 ∙ λ1 + λ2 - 1 ≥ 0

dL(X,λ)/ λ1 = 3 ∙ x1 + 2 ∙ x2 -24 ≤ 0

dL(X,λ)/ λ2 = x1+2 ∙ x2 -15 ≤ 0

условия Куна-Таккера

x1 ∙ dL(X,λ)/dx1 = x1 ∙ (2 ∙ x1 + 3 ∙ λ1 + λ2 – 6) = 0 (a)

x2 ∙ dL(X,λ)/dx2 = x2 ∙ (2 ∙ λ1 + λ2 – 1) = 0 (b)

λ1 ∙ dL(X,λ)/ λ1 = λ1 ∙ (3 ∙ x1 + 2 ∙ x2 -24) = 0 (c)

λ2 ∙ dL(X,λ)/ λ2 = λ2 ∙ (x1+2 ∙ x2 -15) = 0 (d)

Решаем методом свертки

пусть λ1 = 0 тогда из (b) λ2 = 1

из (a) x1 = 2,5

из (d) x2 = 6,25

Проверяем полученные координаты по условию Куна-Таккера

x1 ∙ dL(X,λ)/dx1 = 2,5 ∙ (2 ∙ 2,5 + 3 ∙ 0 + 1 – 6) = 0 (a)

x2 ∙ dL(X,λ)/dx2 = 6,25 ∙ (2 ∙ 0 + 1 – 1) = 0 (b)

λ1 ∙ dL(X,λ)/ λ1 = 0 ∙ (3 ∙ 2,5 + 2 ∙ 6,25 -24) = 0 (c)

λ2 ∙ dL(X,λ)/ λ2 = 1 ∙ (2,5+2 ∙ 6,25 -15) = 0 (d)

Условия выполняются. Подставив полученные значения в целевую функцию получим максимальное значение функции в данной точке :

Max φ(X)=15

Решение проиллюстрируем графически :

Задача 4

Составить вектор функции и матрицу Якоби

Max φ(X)=x1 + 4 ∙ x2 + x1 ∙ x2 – 2 ∙ x1² – 2 ∙ x2²

x1 + 2 ∙ x2 ≤ 12

3 ∙ x1 + x2 ≤ 15

Строим функцию Лагранжа

L(X,λ) = x1 + 4 ∙ x2 + x1 ∙ x2 – 2 ∙ x1² – 2 ∙ x2²+ λ1 ∙ (x1 + 2 ∙ x2 -12)+ λ2 ∙ (3 ∙ x1 + x2 -15)

условия Куна-Таккера

x1 ∙ dL(X,λ)/dx1 = x1 ∙ (1+x2 – 4 ∙ x1 - λ1 – 3 ∙ λ2) = 0

x2 ∙ dL(X,λ)/dx2 = x2 ∙ (4+x1 – 4 ∙ x2 – 2 ∙ λ1 – λ2) = 0

λ1 ∙ dL(X,λ)/ λ1 = λ1 ∙ (x1 + 2 ∙ x2 -12) = 0

λ2 ∙ dL(X,λ)/ λ2 = λ2 ∙ (3 ∙ x1 + x2 -15) = 0

Строим вектор функции :

F(X,λ) =[x1 ∙ (1+x2 – 4 ∙ x1 - λ1 – 3 ∙ λ2) ; x2 ∙ (4+x1 – 4 ∙ x2 – 2 ∙ λ1 – λ2) ;

λ1 ∙ (x1 + 2 ∙ x2 -12) ; λ2 ∙ (3 ∙ x1 + x2 -15)]

Строим матрицу Якоби W(X,λ) :

1+x2 – 8 ∙ x1 - λ1 – 3 ∙ λ2	x1	-x1	-3 ∙ x1
x2	4+x1 – 8 ∙ x2 – 2 ∙ λ1 – λ2	-2 ∙ x2	-x2
λ1	2 ∙ λ1	x1 + 2 ∙ x2 -12	0
3 ∙ λ2	λ2	0	3 ∙ x1 + x2 -15

Алгоритм решения задачи