1 Data transmission systems

1.1 Classification of basic error-correcting codes

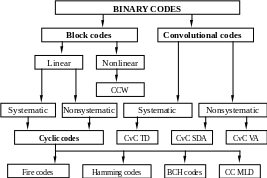Currently the large number of the codes correcting errors are known, that are used for transmitting of discrete messages, and that’s why their systematization and classification are very difficult. At the construction of classification diagram (figure 1.1) examined only those codes that find most application in the data transmission systems.

Figure 1.1 – Classification of basic error-correcting codes

Binary error-correcting codes can be divided into two great classes: block and convolutional. Block codes are codes, in which encoding and decoding are carried out within a block consisting of the specified number of code symbols. Convolutional are codes, in which encoding and decoding processes are continuous, without explicit allocation limits for the construction of the code signal.

Block codes are divided into linear and nonlinear. Linear codes are those in which the construction of blocks, i.e. coding, is performed using linear operations over information symbols. Otherwise, the error-correcting codes are named nonlinear. The simplest example of a nonlinear code is the international code of seven elements, which is called the code with constant weight (CCW), in which each codeword has three units and four zeros in all possible combinations.

Linear codes are divided into systematic and nonsystematic. In systematic codes, information symbols at the output of the encoder are represented explicitly. Belonging to a systematic or nonsystematic code is determined by the choice of the code and the coding algorithm. A significant part of the linear codes occupy cyclic codes (CC), which find wide application in communication systems. The large number of correcting codes belong to CC, among that most known are: Hamming codes, BCH codes, group of codes with the majority-logical decoding (MLD), Fire codes.

Convolutional codes (CvC) also can be divided into systematic and nonsystematic. The first (systematic) are most often decoded by a threshold method (Threshold decoding – TD), and the second (nonsystematic) - with the using of sequential decoding algorithm (SDA) or the Viterbi algorithm (VA). Currently nonsystematic convolutional codes decoded by Viterbi algorithm, are widely used in communication systems.

1.2 Cyclic codes

1.2.1 Basic construction principles of cyclic codes

Cyclic codes were originally created to simplify the encoding and decoding schemes. Subsequently their high corrective properties was detected, thus providing its wide application in practice and, in particular, the wide application in modern telecommunication technologies.

In the construction of CC, code combinations are taken to represent in the polynomial form:

, (1.1)

where – coefficients, specifying values 0 or 1.

For example, the code combination 1100101 can be written as

The main property of CC is the follow: the cyclic shift of single elements of the permitted combination also results to the permitted code combination. Thus, if the combination 1000111 is permitted combination, then combinations 0001111, 0011110, ... are permitted.

Cyclic codes are determined with the generator polynomials P(x) of degree r. The generator matrix of CC can be formed from the generator polynomial by a cyclic shift of the last:

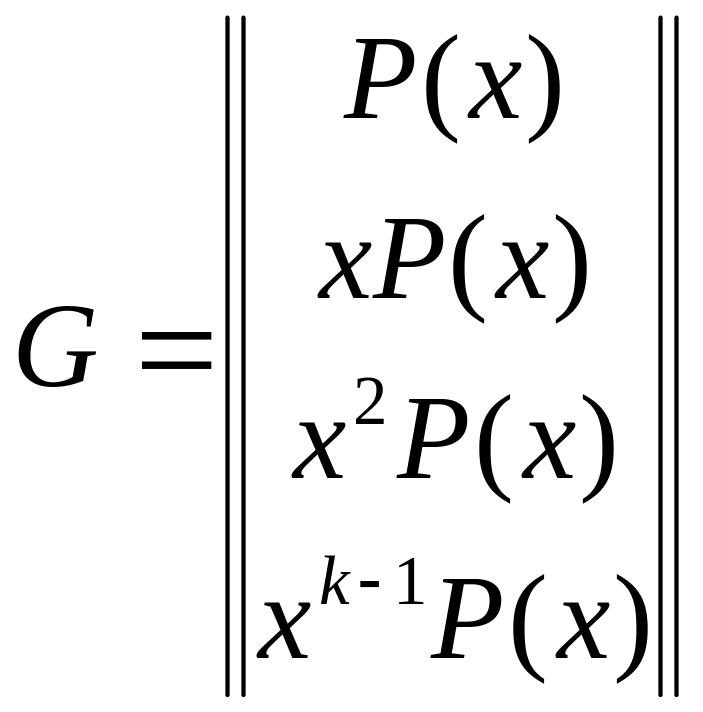(1.2)

Directly from the generator matrix implies that all permitted combinations of a cyclic code can be divided into generator polynomial without remainder. Because of this fact, it is a very easy to determine is the received code combination permitted or not.

In order to have necessary characteristics of the polynomials that representing code combinations of cyclic code, implementation of terms that represent properties of the generator polynomial Р(х) is needed:

• generator polynomial P(x) must be irreducible (in this case the generator polynomial divides without remainder only to itself);

• binomial of type must be divisible by a generator polynomial P(x) without remainder (that is the normal operation of division).

Let’s consider the process of forming code combination of CC. Each codeword G(x) multiplied by , then divide by generator polynomial of degree r (the amount of check bits). As a result of multiplying the degree of each member, included in the polynomial G(x), increases by r. In the division of product on P(x) we take quotient Q(x) the same degree as G(x). In addition, if the product is not divided by P(x), then you have the remainder R(x):

(1.3)

where the sign denotes XOR (addition modulo 2).

As quotient Q(x) has the same degree as G(x), then it is also a combination of simple k-elements code. Multiplying both sides of the equality (1.3) by P(x), we have

(1.4)

Thus, the codeword of a cyclic code can be obtained in two ways:

1. Multiplying the k-element combinations of simple code by generator polynomial P(x);

2. Multiplying the k-element codeword of simple code by the monomial and adding R(x).

The first method leads to the formation of inseparable cyclic code. Inseparability greatly complicates the decoding process, so in practice, the second method of constructing codeword of cyclic code is used.

Code combinations should be different from each other by interchange and the presence of units and zeros. As an option, which makes it possible to distinguish the code combinations from each other, is the code distance (Hamming distance). The code distance between the combinations determined by the number of units obtained after addition modulo 2. For redundant codes, including cyclic, the code distance between the code combinations should always be not less than the minimum code distance.

Minimum code distance is associated with the number of detecting and correcting errors as follows:

(1.5)

, (1.6)

where – the amount of detected errors;

– the amount of correcting errors;

– minimum code distance.

To correct all errors of multiplicity up and simultaneous detection of all errors of multiplicity no more code distance must satisfy the condition

Minimum code distance is only partially describes the corrective properties of redundant code, then they allow to detect and correct errors of higher multiplicity than provided in the calculation of the code parameters. The number of permitted code combinations is determined by the number of data bits and is equal

where n – the length of the code combination;

k – the length of information part of the code combination;

r – the number of check bits.

Thus, the number of permitted combinations in times less than the total number of combinations.

Redundancy of the code is the relation ρ = r/n. The question of the minimum necessary redundancy of the code for the given minimum code distance and length of the code is still pending. There are only a number of upper and lower edges (limits) of amount of check bits of correction codes, which are listed below:

Hamming edge 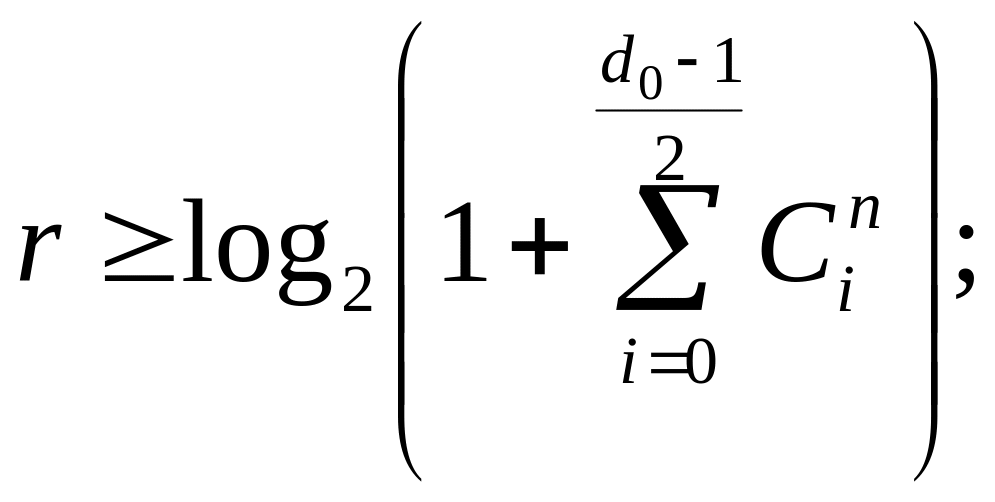(1.7)

Upper Plotkin edge (1.8)

Elias edge where 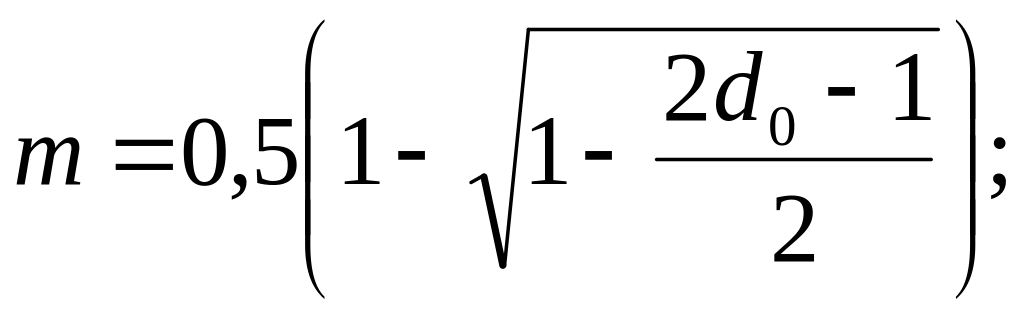(1.9)

Lower Varshamov-Gilbert edge , or . (1.10)

The most optimal approach provides a criterion Varshamov-Gilbert edge.

Knowing the length of information part of a cyclic code, selecting the amount of check bits by the formula (1.10), we can easily calculate the main parameters of a cyclic code: n, k, r, as n = k + r. In a special table (see Table 1.1) for calculated parameters we can choose a polynomial P(x) – and eventually build a codec of the cyclic code.

Table 1.1 – Generator polynomial of cyclic codes

Degree of a generator polynomial	Kind of polynomial
1	x+1
2	x^2+x+1
3	x^3+x+1; x^3+x^2+1
4	x^4+x+1; x^4+x^3+1; x^4+x^3+x^2+x+1
5	x^5+x^3+1; x^5+x^3+x^2+1; x^5+x^4+x^2+x+1; x^5+x^4+x^3+x^2+1
7	x^7+x^3+1; x^7+x^4+x^3+1; x^7+x^3+x^2+x+1
8	x^8+x^4+x^3+x+1; x^8+x^5+x^4+x^3+1; x^8+x^7+x^5+x+1
9	x^9+x^4+x^2+x+1; x^9+x^5+x^3+x^2+1; x^9+x^6+x^3+x+1
10	x^10+x^3+1; x^10+x^4+x^3+x+1; x^10+x^8+x^3+x^2+1
11	x^11+x^2+1; x^11+x^7+x^3+x^2+1; x^11+x^8+x^5+x^2+1
12	x^12+x^6+x^4+x+1; x^12+x^9+x^3+x^2+1; x^12+x^11+x^6+x^4+x^2+x+1
13	x^13+x^4+x^3+1; x^13+x^10+x^9+x+1; x^13+x^12+x^11+x^2+1
14	x^14+x^13+x^11+x^9+1; x^14+x^12+x^10+x^4+x^2+x+1; x^14+x^12+x^2+x+1
15	x^15+x^12+x^3+x+1; x^15+x^13+x^5+x+1; x^15+x^14+x^13+x^10+x^2+x+1
16	x^16+x^15+x^7+x^2+1; x^16+x^14+x^12+x^3+x^2+x+1; x^16+x^12+x^5+x+1

The parameters of CC include:

• n – the length of the code combination;

• k – the length of information part of the code combination;

• r – the length of the check part of the code combination;

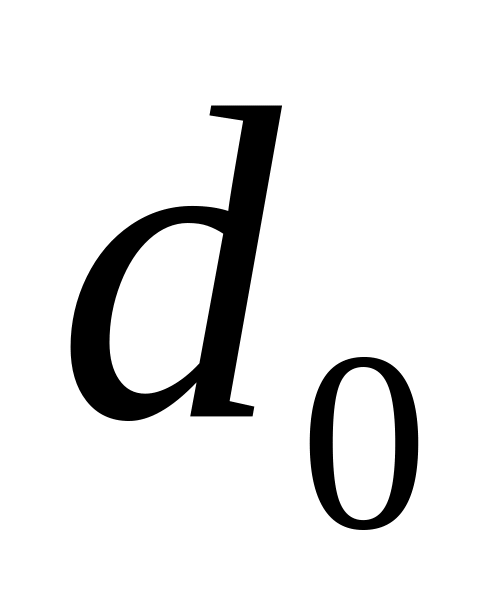• – minimum code distance;

• P(x) – generator polynomial of a cyclic code.