2.1. Метод прямокутників

Метод прямокутників - найпростіший прийом чисельного інтегрування, в якому функція (x) замінюється інтерполяційним багаточленом нульового порядку.

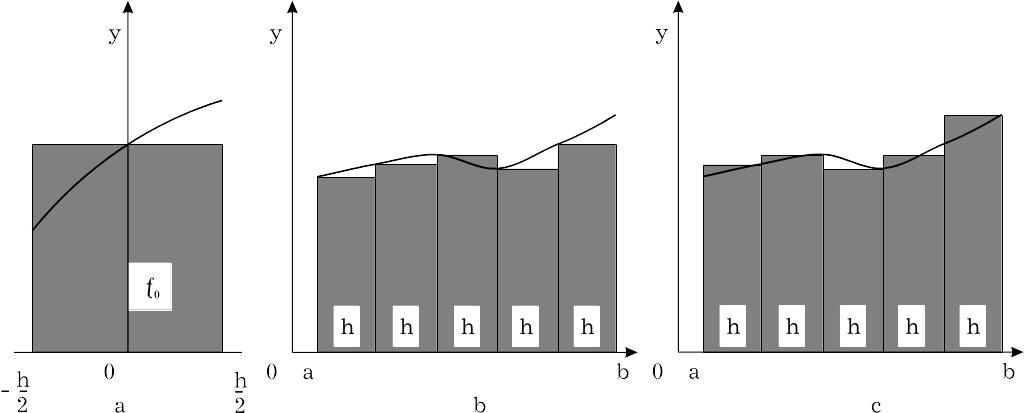
Рис. 5.

Функцію (x) на інтервалі [-h/2,h/2] (Рис.5,а) можна замінити на ₀=const, тоді

Це і є формула прямокутників, тобто S1 = _0* h

Для підвищення точності інтегрування відрізок [а, b] розбивається на m частин і формула прямокутників застосовується до кожного відрізку, на якому значення функції (x) замінюється константою.

формула лівих прямокутників (Рис.5,в)

формула правих прямокутників (Рис.5,с)

2.2. Метод трапецій

Метод трапецій полягає в заміні функції (x) на інтервалі [а,b] інтерполяційним багаточленом першого порядку (лінійна інтерполяція), Рис. 6,а

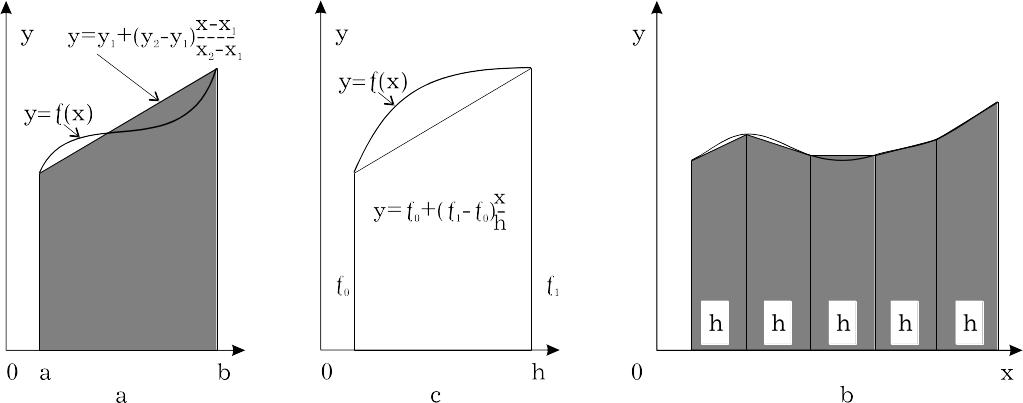
Рис.6

Функцію (x) на інтервалі [0,h] можна замінити інтерполяційним багаточленом першого ступеня у формі Лагранжа або Ньютона:

(x)₀₊₍_1-₀)*x/h )

тоді

а це і є площа прямокутників

Для підвищення точності інтерполяції відрізок [а,b] розбивається на m частин і формула трапецій застосовується до кожного відрізка, на якому значення функції f(x) замінюється інтерполяційним багаточленом першого ступеня (Рис. 6,в)

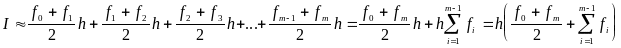
0. Метод парабол (Симпсона)

Метод парабол полягає в заміні функції (x) на інтервалі [а,b] інтерполяційним багаточленом другого порядку (квадратична інтерполяція) Рис. 7.а. Парабола проходить через крапки з координатами (-h _-1) ; (0 ₀) ; (h ₁).

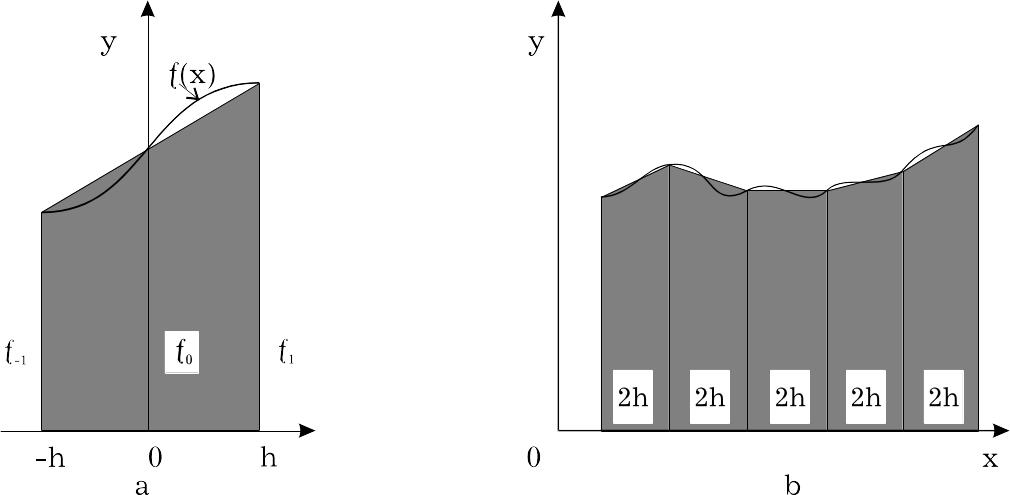
Рис. 7

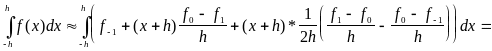
(після розкриття дужок і приведення подібних)

формула парабол

Для підвищення точності інтегрування відрізок [а,b] розбивається на 2m частин і формула парабол застосовується до кожного відрізку [x_2f,x_2f+2], на якому значення функції f(x) замінюється інтерполяційним багаточленом другого ступеня (Рис. 7, в)

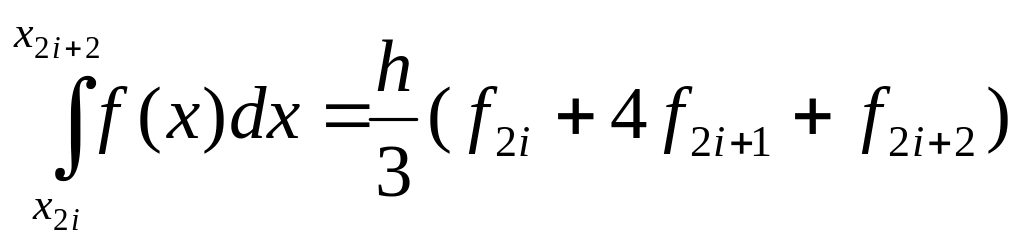
Підсумуємо по всіх інтервалах

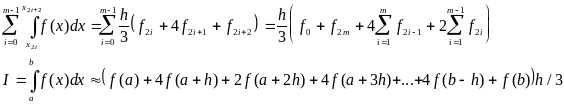
Формулу Симпсона можна записати у вигляді

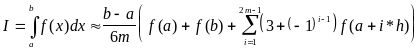
позначивши N=2m, маємо

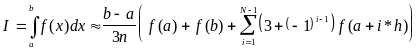
Блок-схеми алгоритмів приведені на рис.8.

Рекомендації. Алгоритм обчислення підінтегральної функції оформити у вигляді функції користувача.

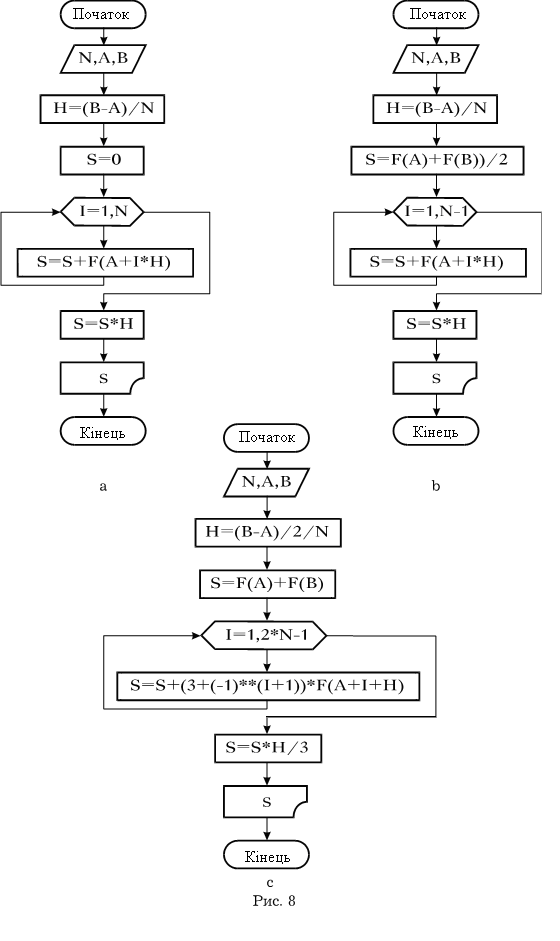
Приклад 1. Обчислення певного інтеграла за допомогою чисельних методів в MathCad.

Індивідуальне завдання 3 Чисельні методи рішення задачі оптимізації

Мета завдання - закріплення теоретичного матеріалу, складання алгоритмів і програм для вирішення задач оптимізації

(x) extr

^{x [a.b]}

Варіанти індивідуальних завдань приведені в табл.. 3.1.

Порядок виконання завдання

1. Представити геометричну інтерпретацію запропонованого вам методу.

2. Скласти алгоритм обчислення оптимального значення функції з точністю E=10^-4

3. Скласти програму на алгоритмічній мові, оформивши вивід результату з відповідними коментарями.

4. Одержати результат, оформити звіт, та представити його до захисту.

Таблиця 3.1.

Варіанти індивідуального завдання 3

Номер варіанту	Досліджувана функція			а	b		Вид екстремуму (min,max)		Метод пошуку екстремуму
1	2			3	4		5		6
1				-1.0	1.0		max		“Золотого перетину”
2	-			-2.0	0.66		extr		Січних
3	2 x sin(x) - cos(x)			-1.0	1.0		extr		Половинного розподілу
4	x2 + 4e-0.25 x			-1.2	1.5		min		“Золотого перетину”
5	x2 + 6e-0.15 x			-2.0	1.0		min		“Золотого перетину”
6	x4 - 0.3 arctg(3.5x)			-1.0	1.0		extr		Ітерацій
7				-2.0	2.0		extr		Половинного розподілу
8	-			-2.5	1.5		min		“Золотого перетину”
9	x (3 + sin(3.6x2)) + 2			0.0	2.0		extr		Ітерацій
10	sin(x2)+ cos(x2) - 10x			-1.0	1.0		extr		Січних
11				-1.0	1.0		min		Половинного розподілу
12	x4 - 1.4 arctg(1.5x)			-1.1	1.5		min		“Золотого перетину”
13	tg(0.5x) - ctg(0.5x)+ x2			0.0	1.0		extr		Половинного розподілу
14	x4 - 0.9 arctg(2x)			-1.0	1.0		min		“Золотого перетину”
15	1 - x + sin(x) - ln(1 + x)			0.0	1.0		extr		Половинного розподілу
16	-e-x ln(x)+ 5x			1.0	5.0		max		“Золотого перетину”
17	ln(x) - x + 1.8			1.0	3.0		max		Половинного розподілу
18				3.0	4.0		extr		Ітерацій
19	x2 tg(x) -1/3			0.0	1.0		extr		Ньютона
20				0.0	2.0		extr		Січних

21	x4 - ln(1+x2)+ tg(x)	-3.0	3.0	min	“Золотого перетину”
22	cos(2/x) - 2sin(1/x)+ 1/x	0.5	3.0	max	Половинного розподілу
23	e-2x -й(0.5x)	-2.0	2.0	min	“ Золотого перетину”
24		0.0	3.0	max	Половинного розподілу
25	x4 - 14x3 + 60x2 -70x	5.0	7.0	extr	Ітерацій
26	x (x-1) 2	-1.0	1.0	extr	Ньютона
27	3 ln2(x)+ 6 ln(x) - 5	-1.0	4.0	extr	Січних
28	0.4 + e|x-3.4|	-1.0	1.0	min	“ Золотого перетину”
29	0.6 + e|x+0.28|	-1.0	1.0	min	“ Золотого перетину”
30	x2 + 10 e0.95x	-1.0	1.0	min	“ Золотого перетину”

Короткі відомості з теорії і основні алгоритми

На практиці часто треба знайти екстремум деякої цільової функції F(x1...xn) n змінних (проектних параметрів).

При формулюванні задачі оптимізації повинні бути визначені наступні компоненти:

a) набір (вектор) змінних x^T = (x₁...x_n) оптимальні значення яких підлягають обчисленню в процесі рішення задачі оптимізації (іноді вектор x називають планом задачі);

б) цільова функція (критерій оптимізації) F(x), чисельне значення якої відображає основну мету виробництва (пов'язана з економічними показниками досліджуваного процесу);

в) обмеження задачі оптимізації, які зв'язані як з обмеженнями на змінні x^T = (x₁...x_n) , тобто з обмеженнями на ресурси, так і з функціональними обмеженнями, що відображають зв'язки в об'єкті.

Сукупність рішень, що задовольняють всім обмеженням, називається допустимою областю (допустимою безліччю задачі). Надалі позначатимемо допустиму область через D. Тоді рішення xD називається допустимим.

Сукупність перерахованих компонент і складає математичну модель задачі оптимізації, яка може бути записана у вигляді:

_

F(x)= extr (1)

xD

Методи рішення задачі оптимізації для функції однієї змінної

1. Методи нульового порядку або методи прямого пошуку, засновані на обчисленнях значень тільки цільової функції (метод дихотомії, ”золотого перетину”).

2. Методи першого порядку або градієнтні методи, в яких при пошуку екстремуму функції використовується точні значення її перших похідних. (метод простих ітерацій і метод хорд для рівняння F'(x)= 0, метод найшвидшого спуску).

3. Методи другого порядку, де разом з похідними першого порядку використовуються і другі похідні цільовій функції (метод Ньютона).

Метод дихотомії

Метод прямого пошуку, заснований на обчисленні самої цільової функції F(x) - min (max)

x[A,B]

А  x  B - прямі обмеження.

Функція F(x) одного параметра описує деяку криву на площині (рис 9 а в) Пошук екстремумів функцій однієї змінної є самостійною і часто зустрічається задачею. Крім того, до нього зводиться набагато більш складна задача пошуку екстремумів функцій безлічі змінних

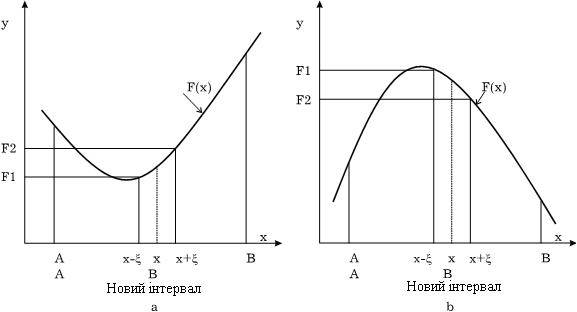
Рис.9

;  - точність визначення екстремуму ;

F1- значення функції в точці x- ;

F2- значення функції в точці x+ ;

Новий інтервал при пошуку min вибирається з умови : якщо F1<F2 (F1>F2), то новий інтервал [А, В=х]; у іншому випадку [А=х,В] [А, В=х] [А=х,В]. (Рис. 9 а)

Новий інтервал при пошуку max вибирається з умови: якщо F1>F2 (F1<F2), то новий інтервал [А, В=х] ([А=х,В]); у іншому випадку [А=х,В] ([А, В=х]) (Рис. 9 в)

Блок-схема алгоритму представлена на Рис. 10.

Параметр С визначає слідуюче:

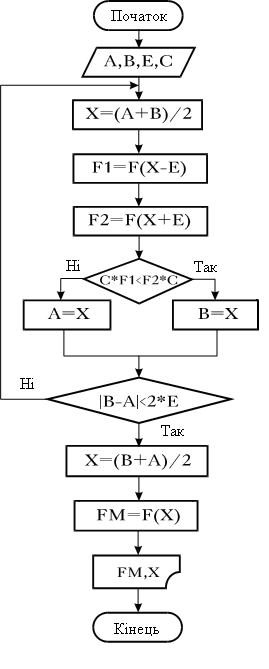
Рис.10

Метод "золотого перетину"

Відрізок [А, В] ділиться за правилом "золотого перетину" : відношення подальших інтервалів постійно

 (1)

Lj-1 = L _j + L _j+1

тобто 

Таким чином t²-t-1=0, звідки 1,618033983

Назва "золотий перетин" похідна від назви відношення в рівнянні (1) .Видно, що Lj_-1 ділиться на дві частини так, що відношення цілого до більшої частини співпадає з відношенням більшої частини до меншої, тобто дорівнює так званому "золотому відношенню".

x₁ = А + B - x₂ x₁ = А + (B-A)(1-1/)

позначимо (1-1/t) через Т1;

Т1 = 0.3819660113, тоді Т2 = 1 - Т1 (1/)

х1 = А + (B-A)Т1

х2 = А + (B-A)Т2

Крапки х₁ і х₂ відстоять на однаковій відстані від кінців інтервалу[А, В](Рис.. 11) . Блок-схема алгоритму методу представлена на Рис. 12.

А, В - межі інтервалу;

х₁ і х₂ - крапки, якими ділиться інтервал А, В за правилом "золотого перетину";

 - точність, з якою обчислюється extr значення функції F(x)

Перевага методу полягає в тому, що обчислюється значення функції лише в одній крапці х₁ або х₂ .

Рекомендація

Обчислення функції оформити у вигляді оператора визначення функції користувача.

Функція F(x) має локальний мінімум в точці х₀, якщо існує деяка позитивна величина Е : якщо | х-х₀ | <E, то F(x)  F(x₀), тобто якщо існує околиця крапки х₀ для всіх значень х в цій околиці F(x) більше F(x₀).

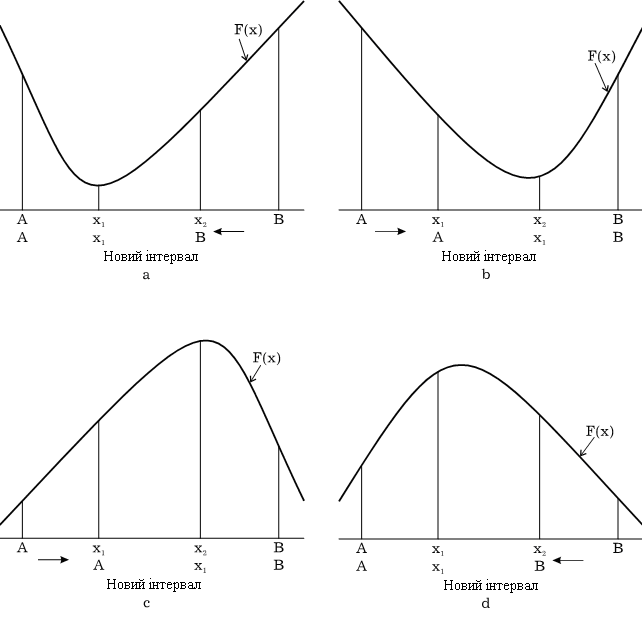
Рис.11

В крапці х₀ F'(x₀)=0 тобто градієнт функції рівний нулю. Позначимо, що в точці х₀ похідна F'(x) міняє знак з від’ємного на позитивний, тобто похідна в min є зростаючою функцією, а оскільки ступінь зростання F'(x) вимірюється другою похідною, можна чекати, що в крапці max F''(x₀) <0, а в крапці min F''>0 (Рис. 13)

Метод Ньютона

Для функції однієї змінної класичний підхід при пошуку значень х в крапках перегину функції F(x) полягає в рішенні рівняння

F'(x)=0 F'(x)=(x)

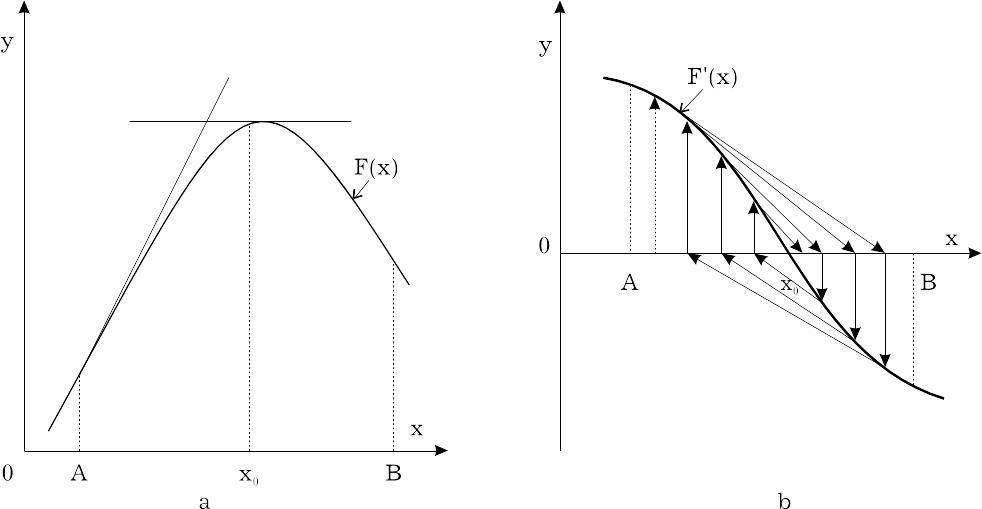
Рис.13

По знаку '(x) судять про крапку х як про max або min. Метод Ньютона заснований на теоремі, якщо існують будь-які А і В : F'(А) і F'(B) мають протилежні знаки, то існує корінь x₀ = [A,B]

Блок-схема алгоритму представлена на Рис. 14. Змінні, які використані:

x - початкове наближення;

х=А, якщо F'(А)F'''(А) >0, інакше х=B;

F1 - значення функції F'(x)

F2 - значення функції F''(x)

FM - значення функції F(x)

Приклад 1. Пошук екстремуму функції в MathCad

Пошук мінімуму функції однієї змінної (для трьох початкових значень х)

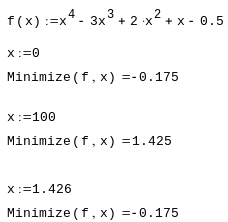
Пошук максимуму функції однієї змінної

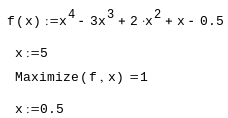
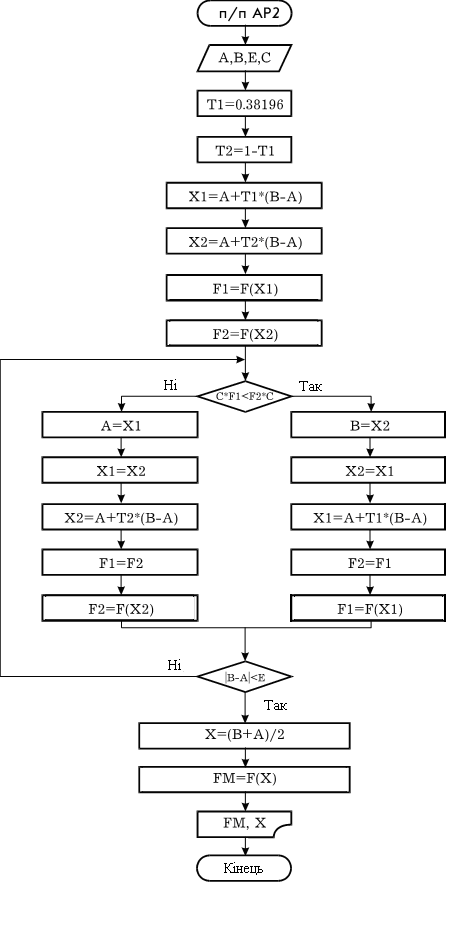
Рис. 14.

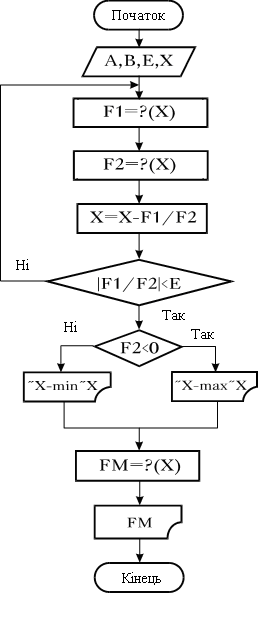
Рис.15