Лабораторная работа № 2 Интерполирование функции полиномом Лагранжа и кубическими сплайнами. Исследование сходимости процесса интерполирования
Постановка задачи.
Пусть на отрезке
[a,b]
задана функция f(x).
Задача интерполирования состоит в том,
чтобы по значениям функции f(x)
в нескольких точках отрезка восстановить
ее значения в остальных точках этого
отрезка. Такая задача допускает сколько
угодно решений в зависимости от
применяемого метода интерполирования.
Необходимо аппроксимировать заданную
функцию с помощью полинома Лагранжа и
кубическими сплайнами. Замена функции
f(x)
интерполяционным многочленом
приводит к
погрешности интерполирования
.
Зависимость погрешности интерполирования
от числа узлов интерполирования
определяет сходимость интерполяционного
процесса.
Интерполяционная формула Лагранжа.
Пусть на отрезке
заданы точки
(узлы интерполирования), в которых
известны значения функции f(x).
Задача интерполирования алгебраическими
многочленами состоит в том, чтобы
построить многочлен
степени n,
значения которого в заданных точках
,
совпадают со значениями функции f(x)
в этих точках.
Многочлен
,
удовлетворяющий условиям:
(1)
называется
интерполяционным
многочленом
для функции f(x),
построенным по узлам
Интерполяционная формула Лагранжа
позволяет представить многочлен
в виде линейной комбинации
значений функции f(x)
в узлах интерполирования. Из условий
интерполирования (1) находится выражение
для коэффициентов
и интерполяционный многочлен Лагранжа
имеет вид
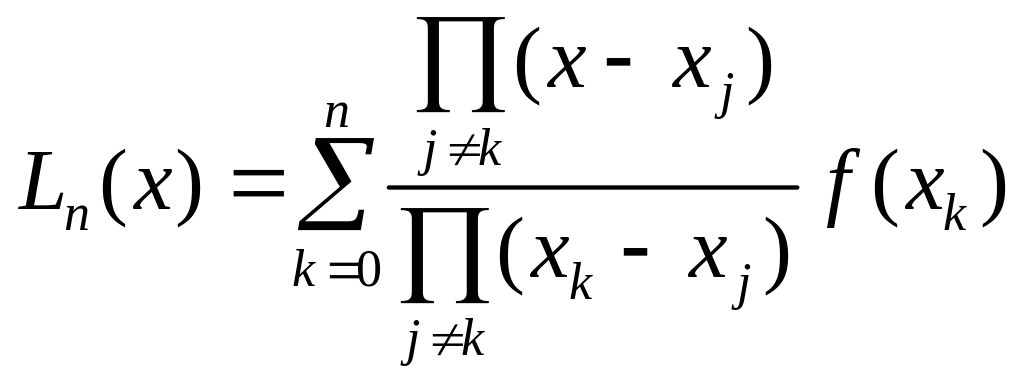. (2)
Максимальная
погрешность интерполирования на отрезке
для
оценивается величиной
,
(3)
где
,
.
Таким образом, интерполирование по формуле Лагранжа имеет n+1 порядок точности.
Интерполяционный
процесс для функции f(x)
сходится в точке
,
если существует
Равномерная сходимость на отрезке [a,b]
означает, что
при
Интерполирование сплайнами.
Интерполирование многочленом Лагранжа с использованием большого числа узлов интерполирования часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений по формуле (2). Для того, чтобы избежать больших погрешностей, весь отрезок [a,b] разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию f(x) многочленом невысокой степени (кусочно-полиномиальная интерполяция). Сплайн-функцией (сплайном) называют кусочно-полиномиальную функцию, определенную на отрезке [a,b] и имеющую на этом отрезке некоторое число непрерывных производных. Кубический сплайн определяется с помощью многочленов третьей степени.
Пусть на [a,b]
задана непрерывная функция f(x).
Введем сетку
с шагом
и обозначим
Сплайном,
соответствующим данной функции f(x)
и данным узлам
,
называется функция s(x),
удовлетворяющая следующим условиям:
1) на каждом сегменте
функция s(x)
является многочленом третьей степени
где коэффициенты
подлежат определению;
2) функция s(x) , а также ее первая и вторая производные непрерывны на [a,b];
3)
(условие интерполирования).
Из условий (1)-(3)
для определения коэффициентов
получается система уравнений
(4)
(5)
Система уравнений (4) имеет трехдиагональную структуру и решается методом прогонки. Остальные коэффициенты определяются по явным формулам (5).
Если
кубический сплайн, построенный для
функции f(x),
то для
справедливы оценки:
Из этих оценок
следует, что при
последовательности
сходятся соответственно к функциям
.
Формулы метода прогонки
Метод прогонки,
являющийся вариантом метода
последовательного исключения неизвестных,
предназначен для численного решения
систем линейных алгебраических уравнений
для
с трехдиагональной матрицей вида
Прямым ходом метода прогонки является вычисление прогоночных коэффициентов по рекуррентным формулам:
На обратном ходе
вычисляются неизвестные значения
:
