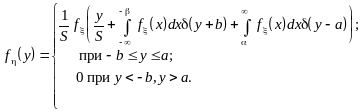10. Чем определяется энергетический спектр на выходе линейной цепи при воздействии на ее вход белого шума?

11. Что такое шумовая полоса пропускания линейной цепи?

12. Чему равняется корреляционная функция процесса на выходе интегрирующей RC-цепочки при воздействии на вход белого шума?

13. Чем определяется отношение сигнал/шум на выходе интегрирующей RC-цепочки?

6. Преобразование случайных процессов в нелинейных радиотехнических цепях

6.1. Безынерционное нелинейное преобразование

Случай безынерционного преобразования самый простой при исследовании нелинейных цепей. При этом сигнал на выходе цепи определяется значением входного сигнала в тот же момент времени :

Здесь некоторая нелинейная функция (рис. 6.1).

Рис. 6.1. Нелинейная цепь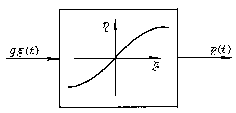

Для аппроксимации функции применяют разные методы. К наиболее употребительным относятся: полиномиальный, метод аппроксимации кусочно-ломанной характеристикой, трансцендентными функциями (экспонентой, синусоидой и т.д.).

Предположим, нам известна ПРВ случайной величины и нам надо найти ПРВ случайной величины в какой-то момент времени t. Предположим снова, что существует однозначная обратная функция . Это справедливо, если - монотонно возрастающая или убывающая функция. Будем при этом исходить из того, что, если величина находится в интервале , то величина обязательно будет в интервале , где (рис. 6.2).

Рис. 6.2. Нелинейное преобразование случайной величины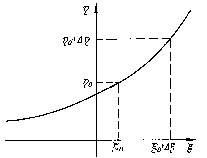

Тогда равны и вероятности этих двух событий:

В этом случае предполагаем, что интервалы и малы и ПРВ в них примерно постоянна. Переходя к пределу , получаем:

или

Поскольку плотность вероятности величина положительная, а в случае убывающей функции производная будет отрицательна, то в формулу надо поставить модуль производной. Таким образом,

Более сложным является случай, когда зависимость не является монотонной функцией. В этом случае не существует однозначной обратной функции : каждому значению соответствует несколько значений . Пусть будут две ветви функции : и (рис. 6.3). В этом случае вероятность попадания на интервал равна сумме вероятностей попадания на интервалы и :

Выразив через , получим окончательное выражение:

Если ветвей обратной функции много, то выражение примет вид:

.

6.2. Распределение процесса на выходе безынерционной цепи с кусочно-линейной характеристикой

Рассмотрим одномерную ПРВ на выходе цепи при аппроксимации ее характеристики с помощью кусочно-линейной функции.

Рассмотрим на примере двухстороннего ограничителя (рис. 6.4) с характеристикой, описываемой выражением

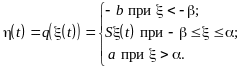
Рис. 6.4. Преобразование случайной величины ограничителем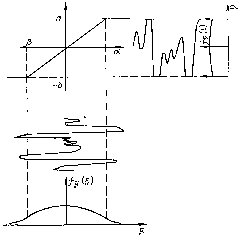

На интервале преобразование линейно, поэтому и, следовательно, , т.е. меняется только масштаб ПРВ величины , а форма распределения остается неизменной. Вероятность того, что случайная величина на выходе ограничителя больше или меньше - b равна нулю. Все значения для которых < преобразуются ограничителем в значение, равное , а все значения < в значение, равное -b.

Следовательно, вероятность того, что случайная величина < , равная

,

сосредотачивается для величины в одной точке =-b, т.е. плотность вероятности в этой точке становится бесконечно большой, в точке =-b появляется дельта-функция. Множитель пропорциональности перед ней равен вероятности . Аналогично будет и для случая, когда < . Таким образом, результирующая ПРВ случайной величины на выходе двухстороннего ограничителя