
Апроксимація (наближення) функцій
Горбійчук, Пістун „ЧМ і моделювання на ЕОМ”
На практиці досить часто бувають випадки, коли неможливо записати зв'язок між "х" та "у" у вигляді деякої залежності у = f(x). Найбільш поширеним випадком, коли вид зв'язку між параметрами х та у невідомий, є задання цього зв'язку у вигляді таблиці {xi, yi}. Цими значеннями можуть бути, наприклад, експериментальні дані. Якщо потрібні значення величини у і в інших точках, то отримувати ці значення кожного разу експериментальним шляхом, не завжди зручно і вигідно. Тому доцільно використати наявні табличні дані для наближеного обчислення значення "у" для деякого проміжногозначення "х".
Ц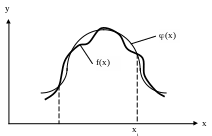 ій
меті служить задача про наближення
функцій: – дану функцію f(x)
потрібно наближено замінити (апроксимувати)
деякою функцією φ(х)
так, щоб відхилення φ(х)
від f(x)
було найменшим. При цьому функція φ(х)
називається апроксимуючою. Основне
питання апроксимації – як вибрати φ(х)
і як оцінити відхилення φ(х)
від f(x).
ій
меті служить задача про наближення
функцій: – дану функцію f(x)
потрібно наближено замінити (апроксимувати)
деякою функцією φ(х)
так, щоб відхилення φ(х)
від f(x)
було найменшим. При цьому функція φ(х)
називається апроксимуючою. Основне
питання апроксимації – як вибрати φ(х)
і як оцінити відхилення φ(х)
від f(x).
Якщо початкова функція задана таблично, тобто на множині окремих точок, то апроксимація називається точковою. Якщо ж початкова функція задана на неперервній множині точок (наприклад, на відрізку [a; b]), то апроксимація називається неперервною.
Інтерполяція
Одним з основних
типів точкової апроксимації
є інтерполяція. Для таблично заданої
функції уі = f(xі)
побудувати функцію φ(х),
яка в заданих точках хі
(![]() )
приймає ті ж значення, що і функція f(x),
тобто φ(хі)
= f(xi),
а в решті точок відрізку [х0;
хn] наближено
представляє f(x)
з деякою похибкою. Точки xі
називають
вузлами інтерполяції, а φ(х)
– інтерполюючою функцією.
)
приймає ті ж значення, що і функція f(x),
тобто φ(хі)
= f(xi),
а в решті точок відрізку [х0;
хn] наближено
представляє f(x)
з деякою похибкою. Точки xі
називають
вузлами інтерполяції, а φ(х)
– інтерполюючою функцією.
На практиці досить часто φ(х) вибирається з класу алгебраїчних поліномів (многочленів)
φ(х)=a0 + a1x + a2x2 +…+ amxm
Інтерполяційні многочлени можуть будуватися як для цілого інтервалу зміни х так і для якоїсь його частини. В останньому випадку інтерполяцію буде кускову (локальну).
Як правило, інтерполяційні многочлени застосовують для обчислення функцій у внутрішніх точках інтервалу х0<х<хn. Однак їх можна використати і для наближеного обчислення функції зовні інтервалу (х<х0 або хn>x). Таке наближення називається екстраполяцією.
Інтерполяція використовується в багатьох прикладних напрямках наук про Землю. У метеорології інтерполюються дані спостережень метеостанціи для одержання карт погоди на великі території. У геології – для побудови 2-вимірних і 3-вимірних моделей підземних масивів за даними точкових забурювань. Чи просто 3-вимірні комп’ютерні моделі рельєфу земної поверхні. Для створення інтерпольованої карти як мінімум необхідний набір точок з даними про їх просторове положення (координати х,у в деякій системі або у вигляді широти/довготи) і кількісне значення параметра z у цих точках – висота, тиск,температура, концентрація забруднення та ін.
Розглянемо
найпростішу задачу інтерполяції, коли
маємо два табличних значення
![]() ,
чи дві точки (
,
чи дві точки (![]() ),
(
),
(![]() )
на площині і потрібно знайти середне
значення. Як відомо результат буде
)
на площині і потрібно знайти середне
значення. Як відомо результат буде
![]() ,
a
,
a
![]() .
Якщо ж потрібно знайти значення
.
Якщо ж потрібно знайти значення
![]() у будь-якій точці
у будь-якій точці
![]() ,
то найпростішим припущенням буде
пропорційна залежність між
та
,
то найпростішим припущенням буде
пропорційна залежність між
та
![]() .
Тоді з подібності трикутників (рис.!)
маємо
.
Тоді з подібності трикутників (рис.!)
маємо
![]() ,
звідки
,
звідки
![]() –
рівняня прямої, що проходить через 2
точки,
(в інших позначеннях
–
рівняня прямої, що проходить через 2
точки,
(в інших позначеннях
![]() ).
).
У
випадку більшої кількості точок, отримані
таким чином проміжні значення утворять
ламану
лінію,
що для певних задач є досить грубим
наближенням, оскільки не виконується
умова гладкості у точках інтерполяції
(![]() ).
(Наприклад
змодельована таким чином поверхня буде
мати вигляд многогранника).
Математично це означає, що у цих точках
похідна такої функції має розриви. Тому
для усунення подібних недоліків потрібно
застосовувати нелінійні
залежності.
).
(Наприклад
змодельована таким чином поверхня буде
мати вигляд многогранника).
Математично це означає, що у цих точках
похідна такої функції має розриви. Тому
для усунення подібних недоліків потрібно
застосовувати нелінійні
залежності.
Розглянемо загальний
випадок. Нехай відомі значення функції
![]() ,
в
,
в
![]() точках.
точках.
xi |
x0 |
x1 |
x2 |
… |
xn |
yi |
y0 |
y1 |
y2 |
… |
yn |
Поставимо
задачу – побудувати алгебраїчний
багаточлен
![]() степеня
степеня
![]() ,
який в точках
,
який в точках
![]() приймає ті ж значення, що й функція
приймає ті ж значення, що й функція
![]() ,
тобто:
,
тобто:
![]() ,
.
(рис.!) (0)
,
.
(рис.!) (0)
Виявляється, що така задача має єдиний розв’язок і такий інтерполяційний многочлен – єдиний, однак форми його запису можуть бути різні.
Запишемо многочлен у загальній формі
![]() (0)
(0)
Оскільки
степінь многочлена
![]() – відома, то задача зводиться до
знаходження його коефіцієнтів.
Найпростіший шлях розв’язку такої
задачі – це використати умови (1) і
скласти систему
– відома, то задача зводиться до
знаходження його коефіцієнтів.
Найпростіший шлях розв’язку такої
задачі – це використати умови (1) і
скласти систему
![]() рівнянь з
невідомими
рівнянь з
невідомими
![]() .
Однак для великих
отримаємо системи з великою кількості
рівнянь і застосування цього методу є
неефективним. Тому для побудови
часто користуються способом Лагранжа.
.
Однак для великих
отримаємо системи з великою кількості
рівнянь і застосування цього методу є
неефективним. Тому для побудови
часто користуються способом Лагранжа.
