Інтерполяція сплайнами

С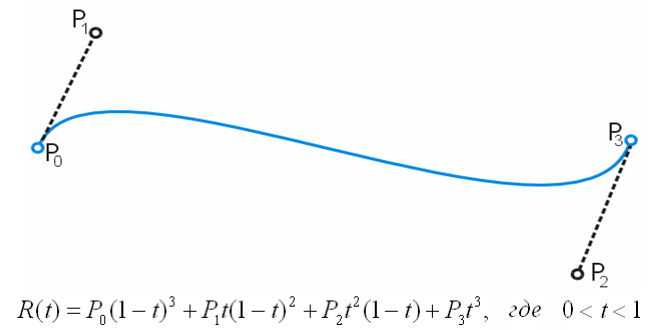 плайн, сплайнова крива – так називають гнучку металеву лінійку — універсальне лекало, що використовується для того, щоб гладко з'єднати окремі точки на кресленні, тобто для графічного виконання інтерполяції. Більше того, крива, що описує деформацію гнучкої лінійки зафіксованої в окремих точках є сплайном. Отже, маємо фізичну модель сплайн-функції (або навпаки сплайн-функція є математичною моделлю гнучкої лінійки). Цей термін прийняли для її віртуального еквівалента; так у комп’ютерній графіці сплайн – це математично розрахована крива або поверхня, яка плавно з’єднує окремі опорні точки. Наибільш поширені сплайни на основі кривих Безьє. (Криві Без'є́ були запроваджені в 1962 році П'єром Без'є з автомобілебудівної компанії «Рено», який використовував їх для комп’ютерного проектування кузовів автомобілів. Таким чином традиційною прикладною сферою використання інтерполяційних сплайнів стали системи автоматизованого проектування).

Сплайни з кривих Без'є використовуються для описування форми символів в шрифтах TrueType. Сплайни також застосовуються в автоматичному картографуванні для побудови цифрових моделей рельєфу.

Означання сплайн-функції. Нехай відрізок розбитий на рівних відрізків , де ; ; .

Сплайном називається функція, яка неперервна на відрізку разом із своїми похідними деякого порядку, а на кожному з відрізків окремо задається алгебраїчним многочленом (як правило на кожн. відрізку іншим).

Тобто основна ідея застосування сплайнів така. Інтервал, на якому відновлюють функцію розбивають на підінтервали, на кожному з яких функцію наближають поліномом досить низького степеня і забезпечують неперервність кривої в точках “склейки” накладаючи умови

Максимальний по всім відрізкам степінь многочленів називається степенем сплайна, а різниця між степенем сплайна та порядком найвищої неперервної на відрізку похідної - дефектом сплайна.

Наприклад, неперервна кусково-лінійна функція (ламана) є сплайном першого степеня з дефектом, що дорівнює одиниці, оскільки неперервною є лише сама функція (похідна нульового порядку), а її перша похідна – це вже розривна функція.

На практиці широке застосування отримали сплайни третього степеня, які мають на відрізку неперервну похідну, щонайменше, першого порядку. Такі сплайни називаються кубічними і позначаються через . Величина називається нахилом сплайна в точці (вузлі) .

Кубичний поліном вибраний тому, що, на відміну, наприклад, від квадратного, забезпечує ідеально плавне з’єднання кривих, якщо вони з’єднуються в точках перегину, тобто в точках нульової кривини лінії, крім того – це крива наинизшей степени, имеющую точку перегиба и имеющую возможность изгибаться [36].

Щоб задати кубічний сплайн на всьому відрізку , потрібно в кожному з вузлів задати значення сплайна та його нахил

Наприклад на -му відрізку отримаємо систему з 4-х рівнянь

що дозволяє однозначно визначити 4 коефіцієнти полінома 3-ї степені . Для полінома 5-ї степені ми повинні додатково накласти умову рівності 2-х похідних на кінцях відрізка і т. д. Наведені вище міркування показують, чому сплайн будують переважно з поліномів непарних степенів (з парною кількістю коефіцієнтів).

Для визначення коефіцієнтів сплайн зручно записувати у вигляді (індекс 3 опускаємо!!!)

тоді отримаємо систему 2-х рівнянь звідки

, , отже .

Можливі також інші форми запису сплайнів. Можна показати, що сплайн , що приймає у вузлах значення, відповідно, , має на частковому відрізку наступний вираз: ( , !!!).

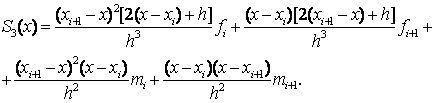
Крива Без'є — параметрическая кривая, задаваемая выражением

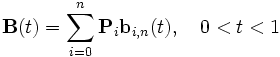где  — опорні вершини, координати яких задаються в 2-х или 3-мерном пространстве, а  — базисные функции кривой Безье, называемые также полиномами Бернштейна.

, де — число комбінацій из n по i, где n — степень полинома, i — порядковый номер опорної вершины.

Також існує рекурсивна формула побудови кривих Без'є

, (індекс внизу означає кількість точок що визначають криву)

Типи кривых Безье

Линейные кривые

П 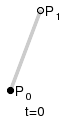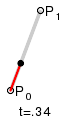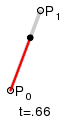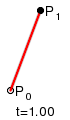ри n = 1 кривая представляет собой отрезок прямой линии, опорные точки P₀ и P₁ определяют его начало и конец. Кривая задаётся уравнением:

.

Очевидно що при , , а при , .

або розписавши ,

тобто параметричне р-ня прямої що прох. через 2 точки.

Параметр t в функции, описывающей линейный случай кривой Безье, определяет где именно на расстоянии от P₀ до P₁ находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P₀ и P₁.

Квадратичные кривые

Квадратичная кривая Безье (n = 2) задаётся 3-мя опорными точками: P₀, P₁ и P₂.

.

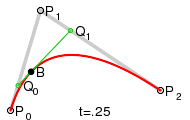
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q₀ и Q₁ (тобто лінійних кривих Без’є ) из условия чтобы параметр t изменялся от 0 до 1:

• Точка Q₀ изменяется от P₀ до P₁ и описывает линейную кривую Безье.

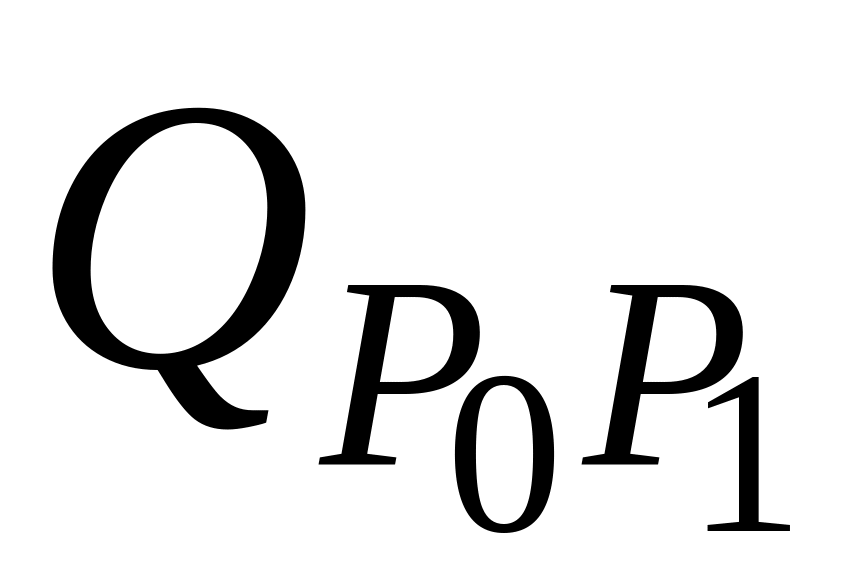
• Точка Q₁ изменяется от P₁ до P₂ и также описывает линейную кривую Безье.

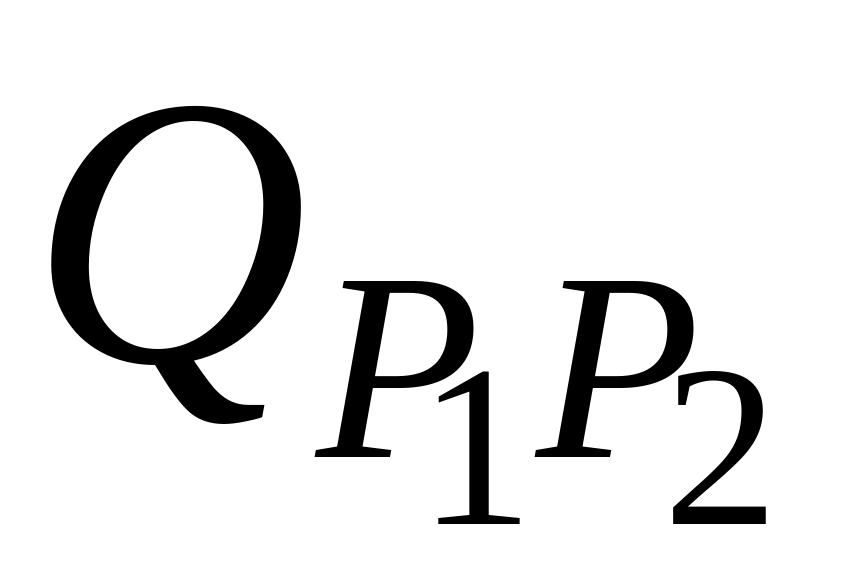
• Точка B изменяется от Q₀ до Q₁ и описывает квадратичную кривую Безье.

• 

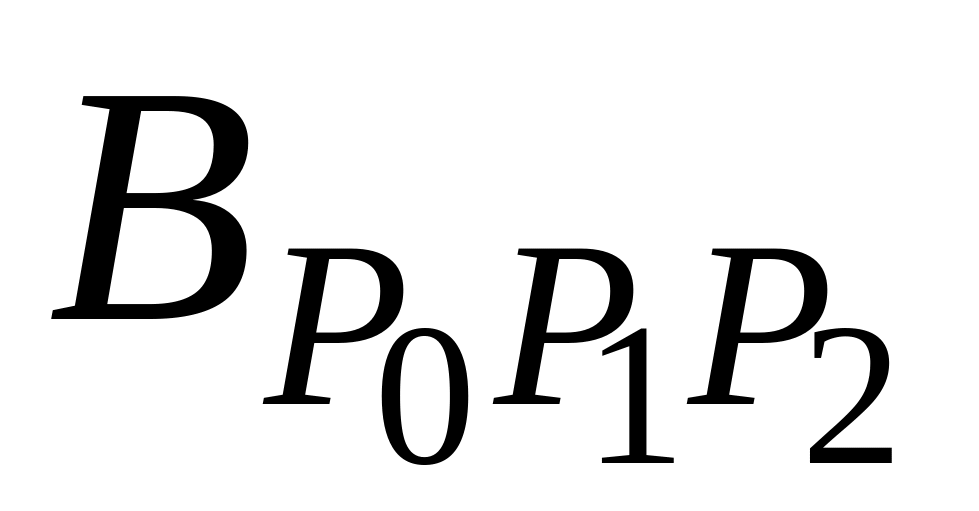
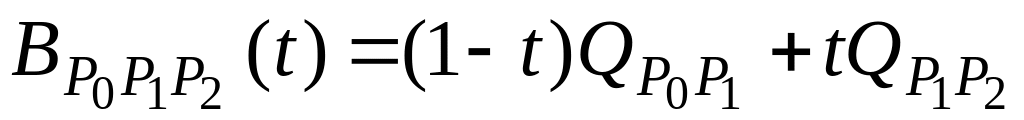
Построение квадратичной кривой Безье

Анимация t: [0; 1]

Очевидно що The velocity vector at t is

B'(t) = -2(1-t)P₀ + 2 (1-t)P₁ - 2 t P₁ + 2t P₂ = 2 [ (1-t) (P₁-P₀) + t (P₂-P₁) ] .

When t=0 the velocity vector is 2(P₁-P₀) and when t=1 it is 2(P₂-P₁). Thus, the path starts at P₀, ends at P₂, and its tangents at P₀ and P₂ intersect at P₁.

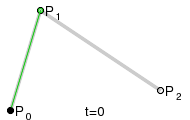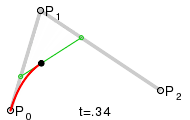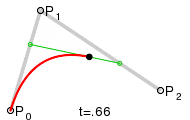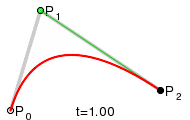
Кубические кривые

В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:

.

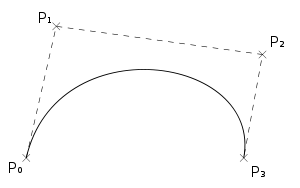
Кубическая кривая Безье

Четыре опорные точки P₀, P₁, P₂ и P₃, заданные в 2-х или 3-мерном пространстве определяют форму кривой.

Линия берёт начало из точки P₀ направляясь к P₁ и заканчивается в точке P₃ подходя к ней со стороны P₂. То есть кривая не проходит через точки P₁ и P₂, они используются для указания её направления. Длина отрезка между P₀ и P₁ определяет, как скоро кривая повернёт к P₃.

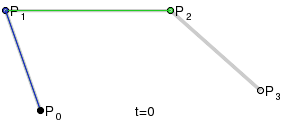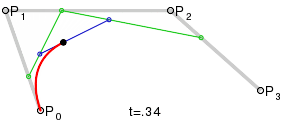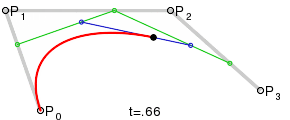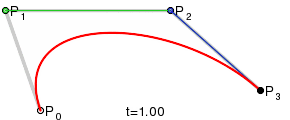
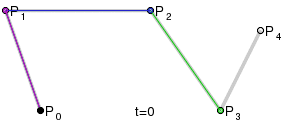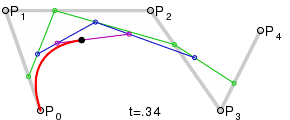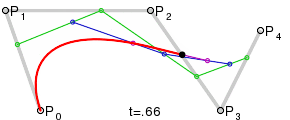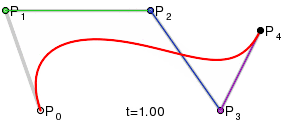
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q₀, Q₁ и Q₂, описывающие линейные кривые, а также точки R₀ и R₁, которые описывают квадратичные кривые: более простое уравнение P0Q0/P0q1=q1p1/p1p2=bq0/q1q0

Построение кубической кривой Безье

Анимация t: [0; 1]

В матричной форме кубическая кривая Безье записывается следующим образом:

,

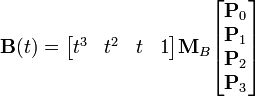где называется базисной матрицей Безье:

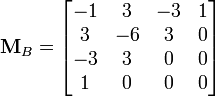
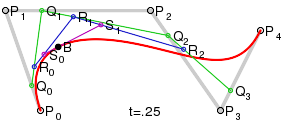
Для кривых четвёртой степени это будут точки Q₀, Q₁, Q₂ и Q₃, описывающие линейные кривые, R₀, R₁ и R₂, которые описывают квадратичные кривые, а также точки S₀ и S₁, описывающие кубические кривые Безье:

Построение кривой Безье 4-й степени