Задача № 7

В данной задаче энергосистему следует представить (рис. 5) в виде двух последовательно соединённых элементов: подсистемы питания потребителя и оставшейся части энергосистемы (районная сеть и электростанция).

Применительно к этим «элементам» возможны четыре гипотезы, образующих полную группу и определяющих их состояние. Для того чтобы найти вероятности этих гипотез можно воспользоваться результатами, полученными при решении задачи № 4. В этой задаче подсчитаны показатели надёжности энергосистемы в целом - Р_С, Q_C и показатели надёжности подсистемы питания потребителя - Р_ПП, Q_ПП. Учитывая схему соединения этих «элементов», показатели надёжности Р_ЭОС, Q_ЭОС первого из них (рис.5) находятся без труда.

Подсчитывать вероятности всех четырёх гипотез, необходимости нет, так как. в дальнейшем интерес представляет только одна из них – «подсистема питания потребителя отказала, а оставшаяся (точнее, «И оставшаяся») часть энергосистемы работоспособна».

При этой гипотезе необходимо определить условную вероятность интересующего события (прекращение электроснабжения потребителя). Нахождение этой условной вероятности вычислений не требует.

По условию задачи исход «опыта» уже известен - электроснабжение потребителя прекратилось. Вероятность такого исхода уже найдена. Теперь требуется переоценить вероятность одной из гипотез (интересующей нас) при известном исходе опыта.

Подобная переоценка производится при помощи формулы Бейеса:

Р(Н_i/А) = ,

где Р(А) - вероятность имевшего место события;

Р(Н_i) – вероятность i-й гипотезы при неизвестном исходе опыта;

Р(А/Н_i) – условная вероятность имевшего место события при i-й гипотезе;

Р(Н_i/А) – вероятность i-й гипотезы, пересчитанная для известного исхода опыта.

Задачи № 8 и 9

Случайными величинами (СВ) называют такие величины (такие количественные результаты опыта), о которых заранее нельзя сказать, какие значения они примут в том или ином опыте

Случайные величины подразделяются на дискретные и непрерывные.

Дискретными называют такие случайные величины, которые в опыте принимают какое-то одно из множества возможных значений, причем эти значения при желании можно перечислить или пронумеровать, т.е. это множество является конечным. Чаще всего (хотя не обязательно) - это целые, неотрицательные значения. Например, количество работоспособных и количество неработоспособных элементов систем электроснабжения, количество перерывов электроснабжения и т.д.

Непрерывными называют такие случайные величины, которые в опыте принимают какое-то одно из возможных значений, причем количество этих значений даже в очень малом интервале бесконечно велико. Иначе говоря, множество возможных значений непрерывной случайной величины является несчётным. Например, уровень напряжения в сети, длительность работы электродвигателя до отказа, ток в линии электропередачи и пр.

Названия случайных величин принято обозначать заглавными буквами латинского алфавита – X, Y; а значения, которые случайные величины принимают в опыте, – строчными - x, y. Например, фразу «напряжение равно 220 В» можно записать следующим образом: U = 220, а фразу «напряжение равно u В»: U = u.

Взаимосвязь между значениями случайной величины и вероятностями их появления устанавливает закон распределения случайной величины. Говорят, что СВ распределена (подчиняется) по тому или иному закону распределения. Существует несколько способов задания закона распределения: ряд распределения, многоугольник распределения, интегральная функция распределения вероятностей, плотность распределения вероятностей и др.

Ряд распределения – это таблица, в которой с одной стороны указаны значения случайной величины, а с другой – их вероятности. В ряду распределения значения случайной величины располагаются упорядочено – по мере их возрастания.

Между всеми возможными значениями случайной величины делится суммарная вероятность этих значений, равная единице. Поэтому сумма всех вероятностей ряда распределения равна единице: = 1

Ряд распределения можно записать только в том случае, если случайная величина является дискретной.

Многоугольник распределения – это графически оформленный ряд распределения. При таком графическом оформлении значения отдельных вероятностей можно было бы не соединять между собой. ломаной линией. Но для увеличения наглядности, чтобы подчеркнуть тенденцию изменения вероятности, их соединяют ломаной пунктирной линией. Пунктирная линия подразумевает, что значения случайной величины – дискретны, и между любой близлежащей парой этих значений других значений нет.

Интегральная функция распределения вероятностей случайной величины - это наиболее универсальный способ задания закона распределения. Его можно применять и для дискретных и для непрерывных случайных величин. Часто, говоря об этом способе, слова «интегральная» и «вероятностей» отбрасывают и используют термин «функция распределения случайной величины» .

Интегральная функция распределения вероятностей представляет собой вероятность того, что некоторая случайная величина Х принимает значение меньшее, чем текущее х: F(х) = Р(Х < х).

Например, если для такой случайной величины, как ток в ЛЭП, функция распределения F(90) = 0,3, то это означает, что вероятность принятия током в ЛЭП значения, меньше 90 А, равна 0,3.

Если для числа отказов в системе электроснабжения интегральная функция распределения F(5) = 0,4, то 0,4 –это вероятность того, что число отказов меньше 5.

Функция распределения вероятностей может быть задана аналитически (в виде формулы), таблично или графически.

Для нахождения значений F(х) к вероятности наименьшего значения случайной величины сначала добавляется вероятность второго значения, затем – третьего и т.д., то есть вероятности как бы накапливаются. Поэтому интегральную функцию распределения иначе называют «функцией накопленных вероятностей».

График интегральной функции дискретной случайной величины - является разрывным (ступенчатым). Скачки соответствуют отдельным дискретным значениям Х, а высоты «ступенек» - соответствующим вероятностям. В местах разрыва функция принимает меньшие значения, т.е. непрерывна слева. В общем виде для дискретной случайной величины можно записать:

F(х) = Р(Х < х) = .

Параметр закона распределения – это числовая характеристика того или иного свойства случайной величины. Важнейшими параметрами являются математическое ожидание и дисперсия.

Математическое ожидание является средним значением СВ (центром распределения СВ) и обозначается – М[Х] или m_Х.

Математическое ожидание дискретной СВ вычисляется как сумма произведений всех n возможных значений х_i этой СВ на вероятности p_i этих значений:

.

Физическая аналогия математического ожидания – абсцисса центра масс системы материальных точек.

По многоугольнику распределения СВ можно приближённо определить математическое ожидание, «на глазок» найдя точку, соответствующую центру тяжести однородного стержня, к которому в точках, соответствующих отдельным значениям СВ, приложены нагрузки пропорциональные вероятностям этих значений.

Математическое ожидание имеет ту же размерность, что и случайная величина.

Важнейшими свойствами математического ожидания являются следующие:

- математическое ожидание неслучайной величины равно этой неслучайной величине;

- неслучайную величину можно выносить за знак математического ожидания;

- математическое ожидание суммы случайных величин равно сумме математических ожиданий этих величин.

Дисперсия случайной величины - характеристика разброса (рассеивания) значений случайной величины около центра распределения

Дисперсия – это второй центральный момент, т.е. математическое ожидание квадрата центрированной случайной величины:

.

Центрированием называется операция нахождения разности между значениями СВ и математическим ожиданием этой величины.

Для нахождения дисперсии дискретной случайной величины может быть использована формула: .

Однако в практических расчетах дисперсию удобнее находить как разность между вторым начальным моментом α₂(х) и квадратом математического ожидания:

D_Х = α₂(х) – m_Х² = М[Х²] - m_Х².

Второй начальный момент ά₂[Х] = М[Х²] = .

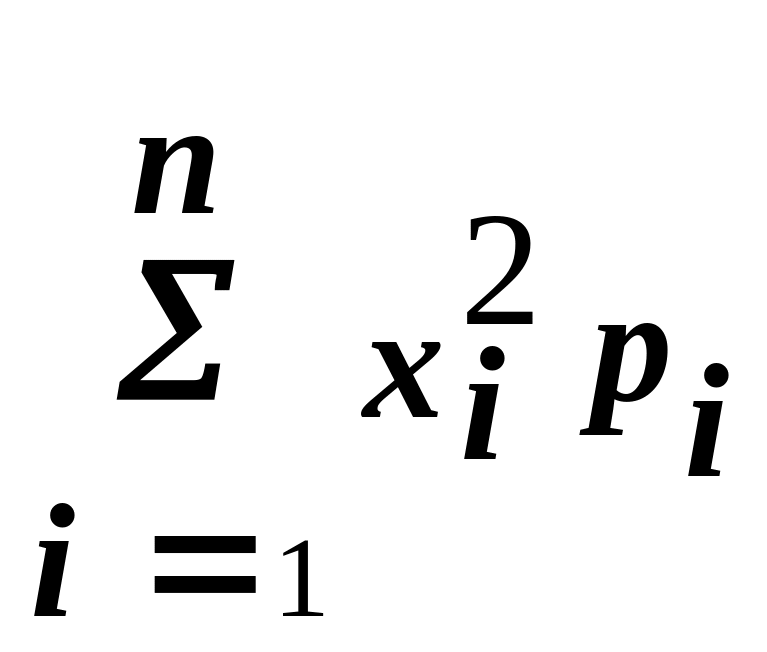Дисперсия принимает любые неотрицательные значения.

Размерность дисперсии равна квадрату размерности случайной величины.

Это свойство дисперсии делает ее неудобным для применения вследствие непривычности получающейся размерности. Например, дисперсия напряжения измеряется в квадратных вольтах, а дисперсия тока в А² и т.д. По этой причине для характеристики рассеивания часто используют среднее квадратическое отклонение (СКО).

Среднее квадратическое отклонение σ_Х является квадратным корнем из дисперсии: .

Размерность СКО совпадает с размерностью СВ.

Важнейшими свойствами дисперсии являются следующие:

• дисперсия неслучайной величины равна нулю;

• неслучайную величину можно выносить за знак дисперсии, возводя её в квадрат;

• дисперсия суммы независимых СВ равна сумме дисперсий этих СВ;

• дисперсия разности независимых СВ равна сумме дисперсий этих СВ;

• дисперсия суммы случайной и неслучайной величины равна дисперсии случайной величины.

Для некоторых широко распространенных законов распределения случайных величин математическое ожидание и дисперсию можно определить более простыми способами, чем указанные выше, применяя полученные для этих законов формулы вычисления основных параметров.

При решении задач 8 и 9 следует принять во внимание, что число отказавших генераторов распределено по биномиальному закону, а количество перерывов электроснабжения - по закону Пуассона, причем биномиальный закон должен быть записан для количества отказавших (а не работающих) генераторов.

Биномиальный закон распределения применим к случайным величинам, которые принимают целые неотрицательные значения: 0, 1, 2, …k …n.

По этому закону будет распределено количество k наблюдений события в серии из n проведенных опытов, если опыты проводятся независимо один от другого и в одинаковых условиях.

В аналитическом виде он задаётся формулой Бернулли (см. задачу №6):

= p^kq^n-k,

где р – это вероятность появления интересующего нас события в опыте, а q – вероятность непоявления этого события в опыте

Для биномиального закона главные параметры можно найти по формулам::

M[k] = np, D[k] = npq.

Закон Пуассона применим к случайным величинам, которые принимают целые неотрицательные значения: 0, 1, 2, …k …n. Причем число n велико (стремится к бесконечности).

В аналитическом виде он задается формулой: P_k= ,

где P_k – вероятность того, что СВ приняла значение равное k;

а - параметр закона Пуассона.

Закон Пуассона является предельным для биномиального, т.е. позволяет вычислять те же вероятности, что и биномиальный закон, но при условии что число опытов стремится к бесконечности, а вероятность появления события в одном опыте стремится к нулю. При этом произведение np = а.

По закону Пуассона так же распределяется количество точек, попадающих на числовую ось, если при этом выполняются условия ординарности, стационарности и независимости (отсутствия последействия). Чаще всего такими точками являются моменты осуществления каких-либо событий, например, отказов в системе электроснабжения.

Характерной особенностью закона Пуассона, отличающей его от других законов, является то, что параметр закона Пуассона одновременно равен и математическому ожиданию и дисперсии случайной величины:

M[k] = D[k] = а.

Для того, чтобы записать ряды распределения по биномиальному закону и закону Пуассона достаточно в одной строке записать первые пять возможных значений случайных величин, а в другой – вычисленные для них по соответствующим формулам вероятности. Для биномиального закона нужно так же вычислить вероятность последнего из возможных значений.

При нахождении параметра а закона Пуассона необходимо использовать значение вероятности безотказной работы (вероятности того, что число отказов равно нулю), полученное при решении задачи № 4 для заданной подстанции. Тогда

P_О = е^-а,

откуда а не сложно определить.

На основании записанных рядов распределения строятся графики: многоугольники распределения и интегральные функции распределения вероятностей.