6.2 Кубічний сплайн

Деяка функція f(x) задана на відрізку  ,що розбитий на частини

 

Кубічним сплайном дефекту 1 називається функція  , яка:

• на кожному відрізку  є многочленом степеня не вище третього;

• має неперервну першу та другу похідні на всьому відрізку  ;

• в точках     виконується рівність 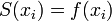  , тобто. сплайн   інтерполює функцію f  в точках  .

Для однозначного задання сплайну вищевказаних умов недостатньо, для побудови сплайна необхідно накласти додаткові вимоги .

Кубічним сплайном називається сплайн,що задовольняє граничним умовам виду:

Теорема: Для будь-якої функції   і будь-якого розбиття відрізка    існує лише один сплайн S(x), ,що задовольняє перечисленим вище умовам.

Ця теорема є наслідком більш загальної теореми Шойнберга-Уітні про умови існування інтерполяційного сплайна.

Побудова

Позначимо: 

На кожному відрізку  функція   є поліномом третього степеня  , коефіцієнти якого треба визначити. Запишемо для зручності   в виді:

тоді

Умови неперервності всіх похідних до 2-го порядку включно записуютьсятак:

а умови інтерполяції в виді

Звідси отримуємо формули для обчислення коефіцієнтів сплайна:

,

Якщо врахувати, що  , то обрахунок   можна провести завдяки  методу прогонки для трьохдіагональної матриці.

7.Задача оберненого інтерполювання

Задача оберненого інтерполювання полягає у знаходженні значення аргументу, що відповідає заданому значенню функції, якого немає в таблиці. Вона обернена до задачі інтерполювання, яка полягає у знаходженні значення функції за аргументом.

Якщо функція   строго монотонна (зростаюча або спадна) на заданій ділянці таблиці, то для неї існує обернена монотонна функція  . У цьому разі обернене інтерполювання зводиться до звичайного інтерполювання для оберненої функції  .

До задачі оберненого інтерполювання відноситься обернене інтерполювання за формулою Гауса.

Інтерполяційна формула Гауса — формула,що використовує в якості вузлів інтерполяції найближчі до точки інтерполювання x узлы . Якщо   , то формула

написана по вузлам  , називається формулою Гауса для інтерполювання вперед, а формула

написана по вузлам  , називається формулою Гауса для інтерполювання назад. В формулах (1) и (2) використані скінченні різниці, що визачаються наступним чином :

Перевага інтерполяційної формули Гауса полягає в тому, що зазначений вибір вузлів інтерполяції забезпечує найкращу оцінку залишкового члена в порівнянні з будь-яким іншим вибором, а впорядкованість вузлів у міру їх близькості до точки інтерполяції зменшує обчислювальну похибку інтерполяції