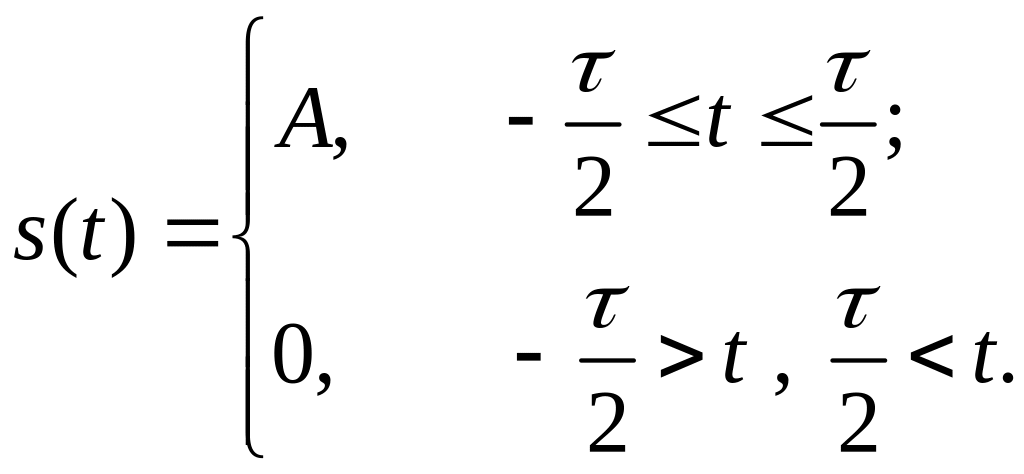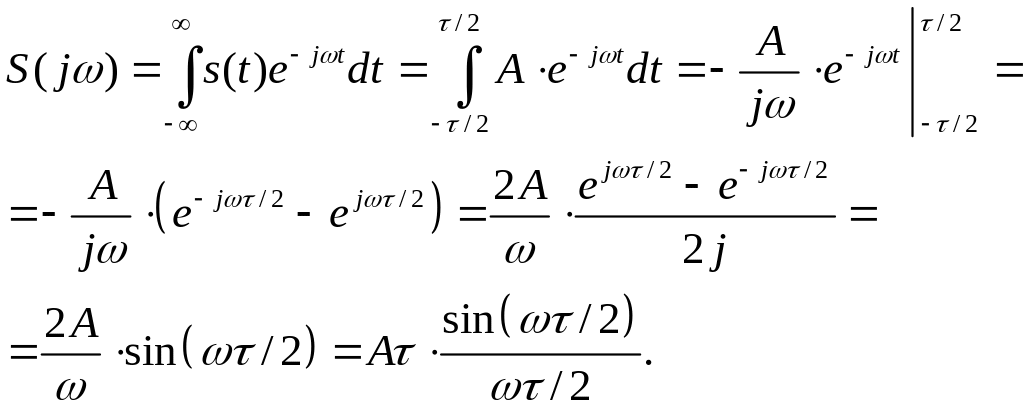1.4 Контрольні запитання і завдання

1. За яких умов періодична функція може бути представлена рядом Фур'є?

2. Які характерні риси має спектр періодичного сигналу?

3. Як можна енергетично тлумачити спектр періодичного сигналу?

4. Що таке перетворення Фур'є?

5. Чим визначається практична ширина спектра періодичної послідовності прямокутних імпульсів за умови, якщо тривалість імпульсів більше половини періоду імпульсів?

6. Які детерміновані сигнали належать до елементарних сигналів?

7. Що розуміють під практичною шириною спектра сигналу? Які критерії використовують для вибору практичної ширини спектра?

Практичне заняття №2 спектри неперіодичних сигналів

2.1 Мета заняття

Метою заняття є вивчення студентами методів спектрального аналізу неперіодичних сигналів.

2.2 Методичні вказівки для самостійної підготовки до заняття [1,3-5].

Будь-який фізичний сигнал є обмеженим у часі та має обмежену енергію згідно з наступною умовою:

(2.1)

де - скінченна величина.

Кожен з неперіодичних сигналів можна розглядати як періодичний з періодом . Завдяки цьому спектральний аналіз періодичних процесів може бути узагальненим і на неперіодичні процеси. При збільшенні інтервали між суміжними частотами у спектрі сигналу та амплітуди спектральних складових зменшуються, а при стають нескінченно малими. При цьому ряд Фур'є, що відображує спектральний опис періодичного сигналу, перетворюється на інтеграл Фур'є, що відображує спектральний опис неперіодичних сигналів.

Нехай , - періодичний та неперіодичний сигнали відповідно. Сигнал відповідає ряду Фур'є:

,	(2.2)
.	(2.3)

При , , , а перетворюється в поточну частоту .

Замінимо суму інтегралом

.

(2.4)

Позначивши інтеграл у квадратних дужках через отримаємо формули прямого й зворотного перетворення Фур'є:

	(2.5)
.	(2.6)

Тут - комплексна спектральна щільність або спектральна характеристика (спектр) неперіодичного сигналу (функція частоти).

Порівнюючи ряд та інтеграл Фур'є, слід зазначити, що, як у випадку ряду, так і у випадку інтеграла Фур'є сигнал може бути представлено у вигляді суми комплексних гармонік з позитивними та негативними частотами.

Комплексні гармоніки ряду мають вигляд

,

де , тобто комплексні амплітуди, що мають кінцеві значення модуля, помножуються на оператор обертання .

Комплексні елементарні гармоніки під знаком інтегралу у виразі (2.6), які мають комплексні амплітуди із нескінченно малим модулем, помножуються на оператор обертання .

На графіках АЧС одиночних сигналів вздовж осі ординат відкладають не амплітуди, а модуль спектральної щільності – відношення нескінченно малої амплітуди до нескінченно малого інтервалу частот, що є кінцевою величиною. На графіках ФЧС одиночних сигналів вздовж осі ординат відкладають аргумент спектральної щільності. Графіки й мають не дискретний, а суцільний характер, тому що частоти зростають неперервно.

Формули для визначення комплексних амплітуд ряду Фур'є (2.3) та обчислення спектральної щільності (2.5) ідентичні. Вони відрізняються друг від друга лише множником і змінною у випадку ряду Фур'є та для інтеграла Фур'є. Межі інтегрування збігаються, тому що в обох випадках вони дорівнюють інтервалу часу, протягом якого функція відмінна від нуля. Функція при одиночному сигналі повинна бути абсолютно інтегрувальною, тобто при досить великому видаленні від її “середини” функція стає нескінченно малою, а межі можуть бути обмежені. Через це між комплексними амплітудами ряду та спектральною щільністю існує наступна залежність:

,

(2.7)

де .

Формула (2.7) означає, що для обчислення комплексних амплітуд ряду Фур'є у випадку періодичного сигналу досить обчислити спектральну щільність одиночного сигналу, з якого утворена періодична послідовність, а потім помножити значення цієї щільності для частот . Це дозволяє переходити від спектра періодичної послідовності імпульсів до спектра відповідного одиночного сигналу і навпаки.

Виділивши дійсну та мниму частини, отримаємо наступну формулу для спектральної щільності сигналу:

,

(2.8)

де , .

Модуль спектральної характеристики визначається співвідношенням

,

(2.9)

і є парною функцією , а фаза спектральної характеристики визначається співвідношенням

.

(2.10)

Функція є непарною до частоти , тому що - парна, а - непарна функції.

Приклад 2.1. Спектр дельта-функції (рис. 2.1).

Рис.2.1 Дельта-функція

Спектр сигналу виду

визначимо, використовуючи формулу (2.5):

.

(2.11)

З урахуванням того, що за допомогою дельта-функції можна відобразити значення реального сигналу в конкретний момент часу у вигляді

,

(2.15)

маємо

.

(2.16)

Отже, АЧС сигналу

,

(2.17)

а ФЧС сигналу

.

(2.18)

Графіки спектрів дельта-функції наведено на рис. 2.2.

Рис.2.2 АЧС і ФЧС дельта-функції

Спектральна щільність дельта-функції на всіх частотах однакова. Цим пояснюється, наприклад, те, що розряд блискавки, що відповідає дельта-функції, створює перешкоди радіоприйому на всіх частотах. Початкові фази елементарних гармонійних складових є такими, що одночасне проходження гармонік через амплітудне значення має місце у момент часу , коли сума гармонік утворює нескінченно велику величину. Для всіх інших значень часу ця сума дорівнює нулю.

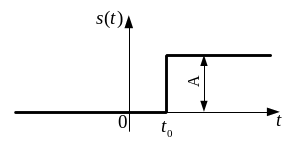
Приклад 2.2. Спектр функції вмикання. Графік сигналу, що описується функцією вмикання

(2.19)

наведено на рис.2.3. Тут 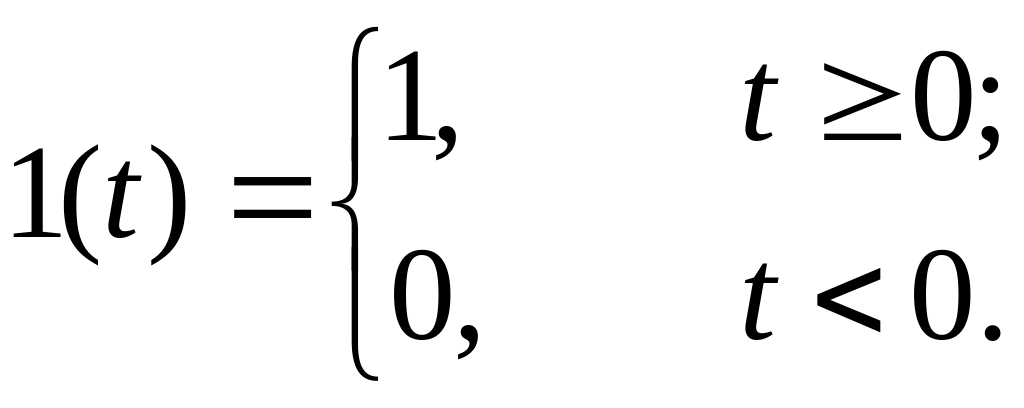- функція Хевісайда.

Рис.2.3 Функція вмикання

Функція вмикання не є абсолютно інтегрувальною, тому застосовувати пряме перетворення Фур'є до цієї функції не можна. Для визначення спектра розглянемо експонентний імпульс

(2.20)

графік якого представлений на рис. 2.4.

Рис.2.4 Експонентний імпульс

Використовуючи (2.5), запишемо формулу для спектральної щільності експонентного імпульсу

Очевидно, що

.

Отже, спектр амплітуд має вигляд:

,

а спектр фаз:

.

Графіки спектрів експонентного імпульсу наведено на рис. 2.5.

Рис.2.5 АЧС і ФЧС експонентного імпульсу

Вихідну функцію вмикання (2.19) можна представити у вигляді експонентної функції (2.20) у якої . Тоді спектральна щільність функції вмикання може бути виражена в такий спосіб:

.

Отже, АЧС та ФЧС функції вмикання має відповідно вигляд:

,
,

де знак “ - ” відповідає області позитивних частот, а знак “+” - області негативних частот.

Графіки спектрів функції вмикання наведені на рис. 2.6.

Рис.2.6 АЧС і ФЧС функції вмикання

Спектральна щільність зростає зі зменшенням частоти. На дуже високих частотах (коротких хвилях) спектральна щільність є малою. Цим пояснюється та обставина, що так звані “промислові перешкоди” радіоприйому найбільш інтенсивні на довгих хвилях. У метровому діапазоні хвиль промислові перешкоди є незначними.

Початкові фази всіх елементарних гармонійних складових дорівнюють , тому гармоніки змінюються за законом синуса. У момент часу відбувається формування переднього фронту функції вмикання.

Графік сигналу, що описується функцією вмикання із запізнюванням, наведено на рис. 2.7.

Рис.2.7. Функція вмикання із запізнюванням

Спектр такого сигналу дорівнює

,

тобто АЧС не змінюється

,

а ФЧС

,

буде відповідати графікові, що наведено на рис. 2.8.

Рис.2.8 ФЧС функції вмикання із запізнюванням

Приклад 2.3. Спектр одиночного прямокутного імпульсу.

(2.20)

Розглянутий сигнал наведено на рис. 2.9.

Рис.2.9 Одиночний прямокутний імпульс

Використовуючи (2.5), запишемо формулу для спектральної щільності одиночного прямокутного імпульсу:

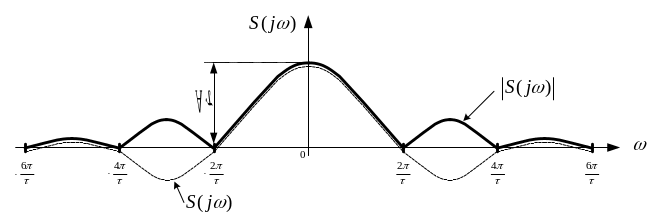
Таким чином, спектр одиночного прямокутного імпульсу (2.20) є речовинним. Його графік визначається законом зміни величини . Ця величина при має максимальне значення, що дорівнює одиниці. Зі зростанням частоти немонотонно зменшується, проходячи через нуль при , де . Графік зміни спектральної щільності наведено на рис. 2.10а пунктиром. Суцільною лінією показано модуль спектральної щільності , тобто амплітудно-частотний спектр. При спектральна щільність дорівнює площі імпульсу . Чим більше ця величина (більше енергія сигналу), тим більше спектральна щільність сигналу.

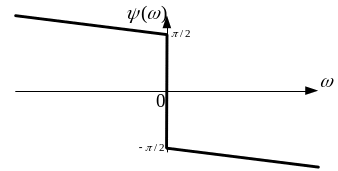
На мал. 2.10б наведено ФЧС одиночного прямокутного імпульсу. Позитивним значенням відповідають початкові фази, що дорівнюють нулю або парному числу , а негативним – початкові фази, що дорівнюють непарному числу .

Слідство. Дельта-функцію можна розглядати як граничну форму прямокутного імпульсу тривалості й амплітуди . Тоді спектральну щільність дельта-функції можна виразити в такий спосіб:

Отже, АЧС сигналу

,

а ФЧС сигналу

.

а)

б)

Рис.2.10. АЧС і ФЧС одиночного прямокутного імпульсу
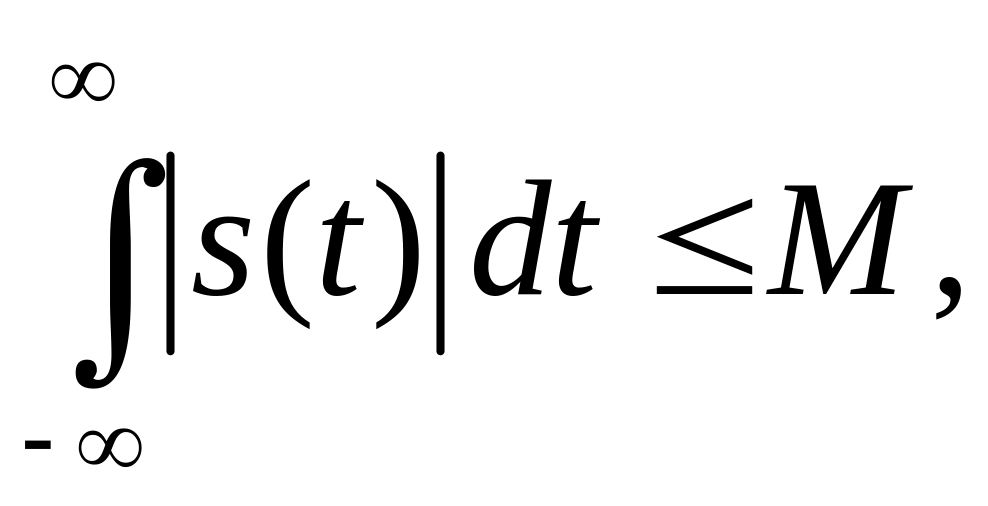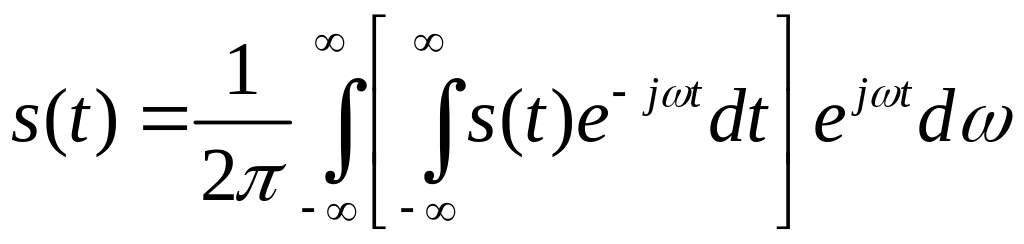
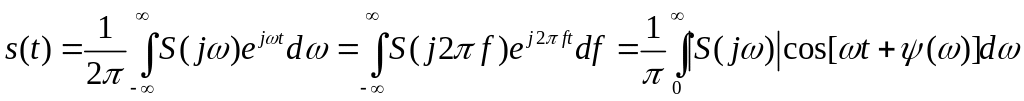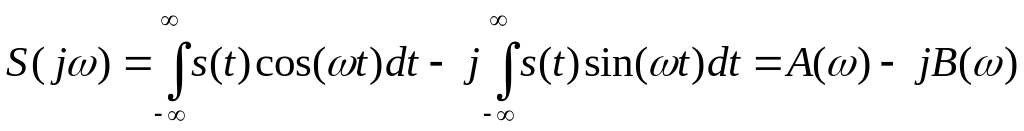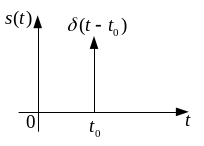
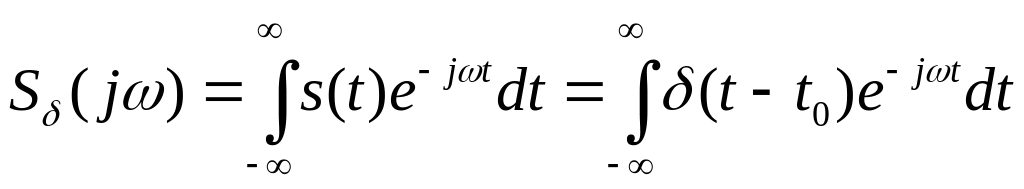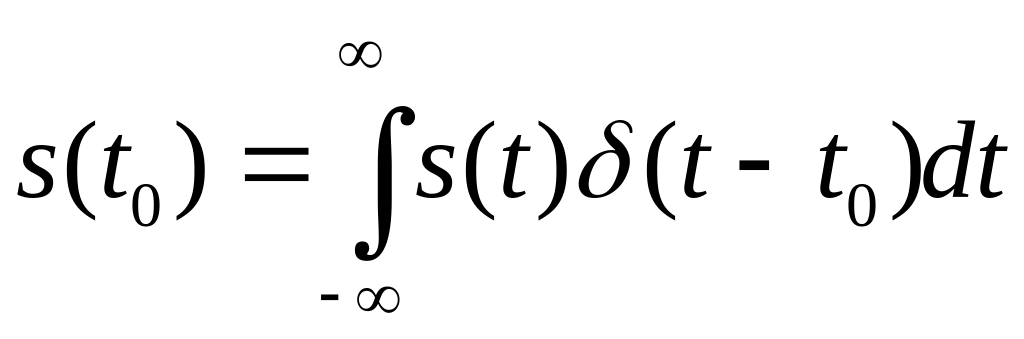
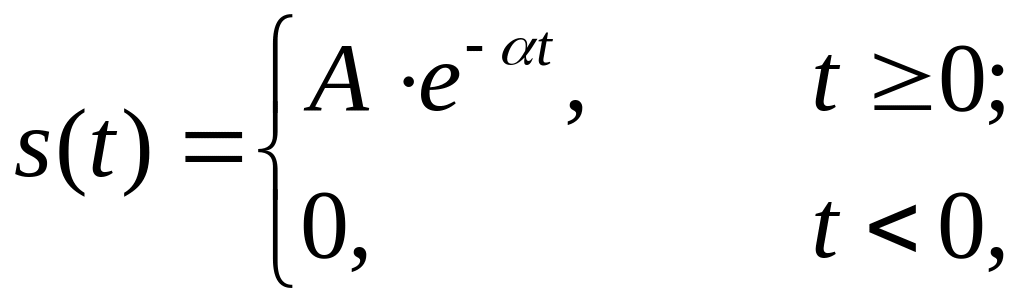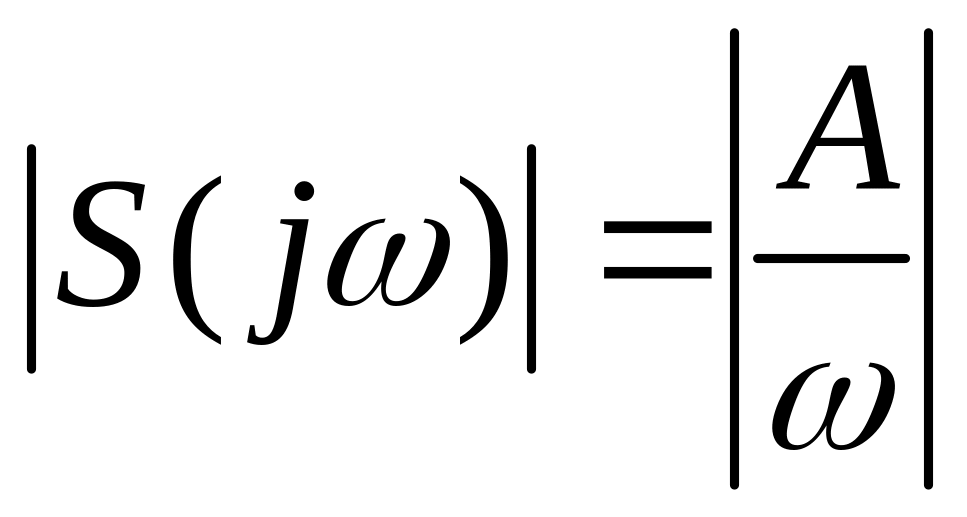
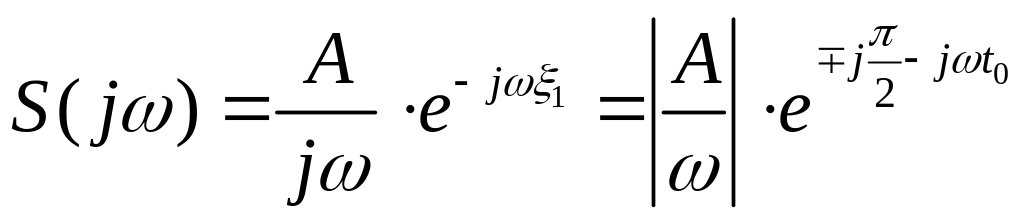