Інтеграл – одне з центральних понять не тільки математичного аналізу, а і всієї математики.

Як відомо з механіки, коли тіло вільно падає в початковий момент часу швидкість тіла дорівнює нулю, то в довільний момент часу тіло пройде шлях

.

Ця формула була знайдена Галілеєм експериментально. За допомогою операції диференціювання знайдемо швидкість у будь-який момент

,

а також прискорення

Більш типовою для механіки є інша, обернена задача: нехай точка рухається вздовж числової вісі, її координата, а її швидкість в момент t. Якщо припустити, що відома функція часу, то необхідно вирахувати для будь-якого за умовою, що задано

Таким чином, по заданій треба знайти функцію , яку називають первісною для функції .

Задачу пошуку первісної можна зустріти і при розв'язанні геометричних задач. Так, у курсі алгебри та аналізу середньої школи введено поняття криволінійної трапеції як фігури, що обмежена графіком функції , відрізками прямих та , і відрізком осі . Якщо на відома первісна для неперервної функції ( , де суцільний проміжок, інтервал, відрізок або напівінтервал), і –шукана площа криволінійної трапеції, то на інтуїтивному рівні, без строгого доведення, одержано

і функція , така, що , а коли  , то площа частини криволінійної трапеції, що лежить зліва від вертикальної прямої, яка проходить через точку , є первісна для . При цьому .

У деяких випадках первісну неважко знайти. При такому підході випливає запитання: якщо розривна функція на , наприклад, , ,

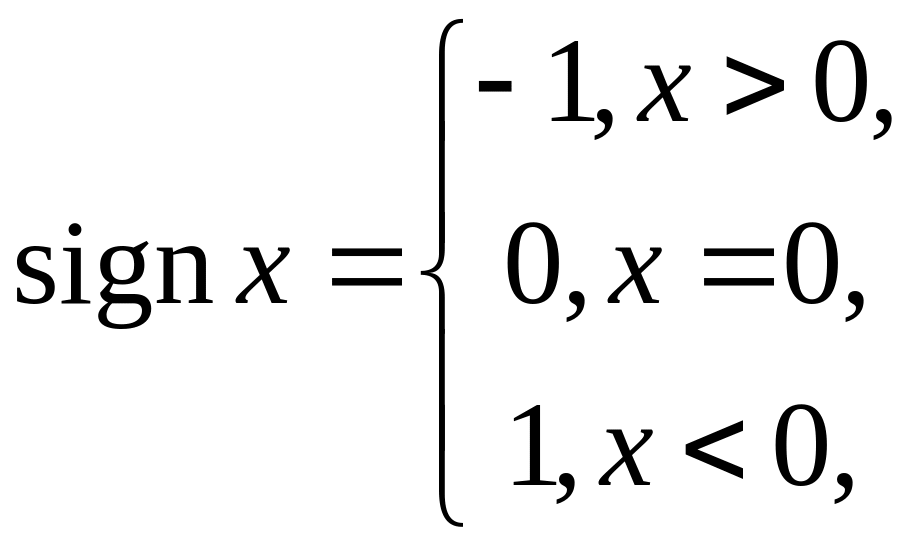
то площу "криволінійної трапеції" легко знайти, а чи існує первісна для цієї функції? А якщо існує, то як її знайти?

В одному із своїх творів Архімед обчислив площу параболічного сегменту . Формули для обчислення площі цієї фігури в геометрії немає. Архімед вважав, що

,

тобто відрізок ділиться на рівних частин і на кожному відрізку криволінійна трапеція замінюється прямокутником з висотою . Тоді

,

а оскільки

,

то

.

Зрозуміло, що чим більше , тим точніше права частина визначає величину . Згідно з Архімедом, величина площі параболічного сегменту між параболою , віссю на дорівнює .

Створення інтегрального числення з його виходами в геометрію, механіку, фізику – діло XVII століття, в основному Ньютона та Лейбніца. Похідну Ньютон називав флюксією, а первісну – флюєнтою. Лейбніцу належать позначення і , а також правила невизначеного інтегрування.

Якщо Архімед міркував на рівні , то точне значення інтеграла як границі інтегральних сум вперше дав Коші (1821). Саме він поставив запитання про існування інтеграла від неперервної функції, але його доведення не було коректним. Необхідні та достатні умови інтегруємості не тільки неперервної, а навіть розривної функції, були отримані Ріманом, Лебегом протягом другої половини ХІХ століття. У звя’зку з деякими спеціальними задачами нове поняття інтеграла ввів Стілт’єс в 1894 році, а в 1902 році найбільш широке поняття інтеграла ввів Лебег, яке зробило можливим описання клас у первісних по їх внутрішнім властивостям.

У подальшому інтегральне числення, побудоване тільки для інтеграла Рімана, оскільки теорія інтеграла Лебега потребує теорії міри, є складною для розуміння студентами технічних вузів. Але при дослідженні застосувань інтеграла Рімана будуть розглянуті такі задачі, що приводять до невласних інтегралів. Останні тісно пов'язані з поняттям числових, функціональних, зокрема, степеневих рядів.

Розділ і Невизначений інтеграл

§1. Первісна для функції

Нехай І – множина типу відрізка (сегменту), інтервалу, напівінтервалу скінченного або нескінченного.

Означення 1. Функція називається первісною для функції , якщо існує на І і .

Приклад 1.1 є первісною для на . Дійсно,

.

Приклад 1.2. Функція не буде первісною для на проміжку , оскільки рівність не виконується в точці . Але в кожному з проміжків і функція є первісною для .

Зауваження. При розв’язанні багатьох задач, як правило, мають справу з більш узагальненим випадком. Наприклад, для функції на інтервалі первісною буде . Ця функція невизначена, коли , і тому не можна казати про похідну в точці . Але , коли і , коли , . У зв’язку з цим кажуть, що функція є первісною для на . Взагалі, функцію називають первісною для , , якщо , і , коли , 0. Аналогічно визначається первісна і на проміжках типу .

Відмітимо основні властивості первісної, відомі зі школи.

Теорема 1. Якщо є первісна для функції , то теж буде первісною для функції , де , .

Дійсно,

.

Теорема 2. Якщо і дві первісні для однієї і тієї ж функції , то (кажуть, що вони відрізняються на сталу на множині ).

Дійсно, функція на будь-якому задовольняє умовам теореми Лагранжа , aле , а тому .

Таким чином, загальний вид первісних для функції на проміжку

,

де довільна стала, а одна із первісних для функції на проміжку .

Ця властивість первісних має наступний геометричний зміст: графіки будь-яких двох первісних для функції одержуються один через другий паралельним переносом вздовж осі .

Приклад 1.3. Нехай . Припустимо, що існує первісна , тобто . Тоді , але за визначенням похідної

.

За теоремою Лагранжа , а тому,

,

де між та .

Як відомо, функція , коли х прямує до 0 , не має границі. А тому для функції на множині не існує первісної.

У таких випадках застосовують узагальнену первісну як функцію , де на множині за виключенням скінченої кількості точок із .

За таким означенням неелементарна функція на множині має первісну . Зазначимо, що елементарна функція.

Чи завжди елементарна функція має первісною також елементарну функцію?

Приклад 1.4. Нехай . Функція неперервна на всій числовій осі і

Оскільки повинна бути неперервною на R і на множині для , первісною буде , то коли покладемо для функції , де підберемо так, щоб була неперервною в точці 0.

Оскільки

,

а

,

то, за умови

одержимо, що .

Таким чином, для функції первісною буде

Дійсно, коли , то , а коли , то ,

а тому .

Первісна , визначена формулою (1.1), для елементарної функції , вже не буде елементарною.

§2. Невизначений інтеграл

Операцію переходу від функції до її первісної називають невизначеним інтегруванням і записують символом

який називають невизначеним інтегралом від функції на даному проміжку. Знак називають знаком невизначеного інтеграла, підінтегральною функцією, підінтегральним виразом, змінною інтегрування.

Таким чином, якщо будь-яка первісна для функції на проміжку, то на цьому проміжку

тобто будь-яку іншу первісну можна одержати з конкретної , додаючи деяку сталу.

У відповідності з означенням символу невизначеного інтеграла, він визначає функцію , похідна якої дорівнює підінтегральній функції . Виходячи з цього і законів диференціювання, пропонуємо коротку таблицю невизначених інтегралів, яку можна одержати із таблиці похідних найпростіших елементарних функцій.

;

4) ;

5) ;

6. ;

7. ;

8. ;

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

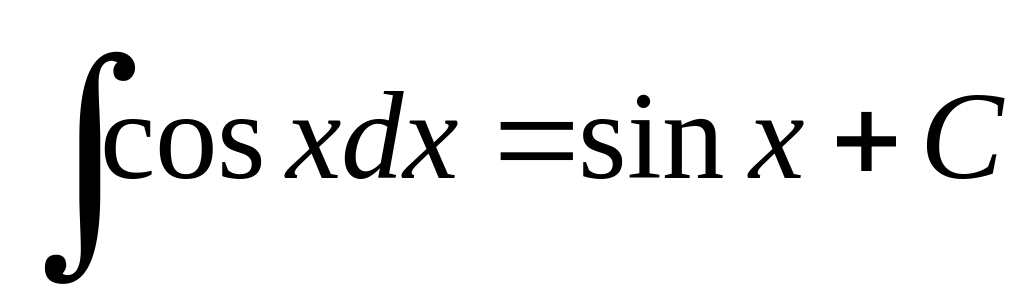Кожна із формул 1)-16) розглядається на тих проміжках із , на яких визначена функція . Якщо таких проміжків декілька, то стала С може змінюватись від одного до іншого проміжку.

Приклад 2.1. Перевіримо, наприклад, вірність формули 12):

Передусім, зробимо важливе зауваження (відоме зі школи як правило 3 знаходження первісної): якщо первісна для функції , то функція є первісна для функції , тобто

А тому:

Приклад 2.2.

Приклад 2.3.

Приклад 2.4.

Приклад 2.5 і т.п.

Поряд з формулами 1)-16) рекомендуємо знати і формули

17)

18)

які досить часто зустрічаються на практиці.

Приклад 2.6.

Приклад 2.7.

Приклад 2.8.

Як наслідок із означення невизначеного інтеграла маємо:

Формули 2) і 3) встановлюють взаємність операції диференціювання і невизначеного інтегрування. Ці операції взаємно обернені з точністю до сталої , що з’являється у формулі 3).

Формула 4) означає, що первісну для лінійної комбінації функцій можна шукати як лінійну комбінацію первісних для цих функцій. Для подальшого домовимося довільну сталу С в формулі 4) писати один раз, яку додають до кінцевого результату.

Приклад 2.9.

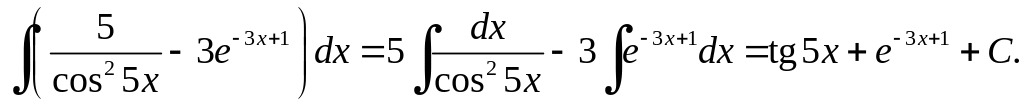
Наведена низка розібраних прикладів показує, що при знаходженні первісних, на відміну від похідних, де достатньо знати таблицю і правила, мало знати таблицю первісних, часто доводиться виконувати різноманітні перетворення.

Більш того, якщо похідною елементарної функції знову є елементарна функція, то перехід до первісної для елементарної функції може привести до функції, яка не є композицією елементарних. У тому випадку, коли первісна існує, але не є елементарною функцією, кажуть, що „невизначений інтеграл

не береться”. Взагалі, клас елементарних функцій визначений досить довільно, як функції, які вивчали у школі. При розв’язанні прикладних задач зустрічаються спеціальні функції, властивості яких вивчені не гірше від , значення табульовані і приведені в посібниках. Прикладом такої функції є інтегральний синус , яка є первісною для функції , такою, що , коли . Інші приклади так званих „інтегралів, що не беруться”, будуть приведені пізніше.