
- •Розділ II Визначений інтеграл
- •§1. Означення визначеного інтеграла за Коші-Ріманом
- •§2. Необхідна умова існування визначеного інтеграла
- •§3. Властивості визначеного інтеграла
- •Приклад 3.1.
- •Звернемо увагу, що зворотне твердження не завжди вірне. Приклад 3.2. Функція
- •§4. Визначений інтеграл зі змінною верхньою границею
- •Основним наслідком цієї леми є
- •§5. Формула Ньютона-Лейбніца
- •Зокрема, коли одержимо
- •§6 Основні правила визначеного інтегрування
- •Приклад 6.1.
- •§7. Деякі нетипові задачі на означений інтеграл
- •§8. Наближені методи обчислення визначених інтегралів
Розділ II Визначений інтеграл
§1. Означення визначеного інтеграла за Коші-Ріманом
Нехай
![]() функція,
визначена на відрізку
функція,
визначена на відрізку
![]() прямої
прямої
![]() зі значеннями в
зі значеннями в
![]() .
Розглянемо спосіб означення інтеграла
від функції
.
Розглянемо спосіб означення інтеграла
від функції
![]() за допомогою сум Коші- Рімана.
за допомогою сум Коші- Рімана.
Будемо
казати, що задається розбиття
![]() сегменту
на частинні інтервали, якщо задані точки
сегменту
на частинні інтервали, якщо задані точки
![]() такі, що
такі, що
![]() ,
,
![]() .
.
Позначимо
через
![]() .
Тоді величину
.
Тоді величину
![]()
називають рангом або діаметром розбиття .
Довільним
чином виберемо по одній точці
![]() на кожному відрізку
на кожному відрізку
![]() ,
та складемо суму виду
,
та складемо суму виду
 .
.
Позначимо
її через
![]() ,
або коротко
,
або коротко
![]() .
Ця сума називається інтегральною
сумою Рімана функції
.
Ця сума називається інтегральною
сумою Рімана функції
![]() на відрізку
.
на відрізку
.
Якщо
невід'ємна
функція на
,
то цілком ясно, що інтегральна сума
приблизно визначає площу криволінійної
трапеції як фігури, що обмежена зверху
графіком функції
![]() ,
знизу − відрізком
осі
,
знизу − відрізком
осі
![]() ,
а з боків відрізками прямих
,
а з боків відрізками прямих
![]() та
та
![]() .
Коли
.
Коли
![]() (тим самим
(тим самим
![]() ),
то зрозуміло, що є сенс вважати: площа
криволінійної трапеції дорівнює границі
інтегральної суми
,
„якщо остання існує”. Відмітимо, що
коли
не завжди
.
),
то зрозуміло, що є сенс вважати: площа
криволінійної трапеції дорівнює границі
інтегральної суми
,
„якщо остання існує”. Відмітимо, що
коли
не завжди
.
Означення.
Дійсне число
![]() називають границею
інтегральної суми
називають границею
інтегральної суми
 ,
коли
,
якщо для будь-якого
,
коли
,
якщо для будь-якого
![]() існує
існує
![]() ,
таке, що для всіх
,
діаметри
,
таке, що для всіх
,
діаметри
![]() яких менші
яких менші
![]() ,
та будь –яких
,
та будь –яких
![]() ,
виконується нерівність
,
виконується нерівність
![]()
або
 .
.
У цьому випадку коротко пишуть
 .
.
Число
називають визначеним
інтегралом
від функції
на відрізку
і позначають
 позначення Лейбніца.
позначення Лейбніца.
Таким чином,
 ,
,
число
![]() називають нижньою границею інтеграла,
називають нижньою границею інтеграла,
![]() верхньою,
верхньою,
![]() змінною
інтегрування,
змінною
інтегрування,
![]() підінтегральною
функцією,
підінтегральною
функцією,
![]() підінтегральним
виразом.
підінтегральним
виразом.
Якщо
для функції
існує
 ,
то функція
називається інтегрованою за Ріманом
на
.
Клас таких функцій позначається через
,
то функція
називається інтегрованою за Ріманом
на
.
Клас таких функцій позначається через
![]() .
.
Отже,
якщо
![]() невід'ємна
функція, то площу
невід'ємна
функція, то площу
![]() криволінійної трапеції можна обчислити
через визначений інтеграл від функції
на відрізку
.
криволінійної трапеції можна обчислити
через визначений інтеграл від функції
на відрізку
.
Відмітимо,
що коли
![]() ,
то для будь якого розбиття
,
то для будь якого розбиття
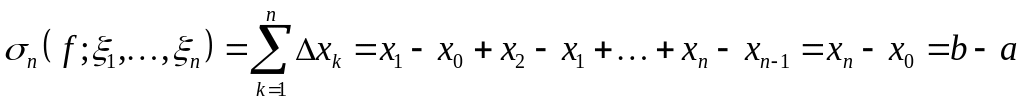 ,
,
а тому

що
зрозуміло з геометричної точки зору:
площа прямокутника зі стороною
![]() та висотою
та висотою
![]() .
.
Зауваження.
Перше означення інтеграла як границі
інтегральних сум належить Коші. Для
неперервної функції
![]() він розглянув суми
він розглянув суми
 ,
,
і довів, що ця послідовність фундаментальна, а тому існує її границя, і поклав
 .
.
Подальше
узагальнення інтеграла належить Ріману,
який замість сум
![]() увів більш загальні суми
увів більш загальні суми
![]() .
.
§2. Необхідна умова існування визначеного інтеграла
Теорема.
Якщо
![]() ,
то функція
обмежена на
.
,
то функція
обмежена на
.
Доведення.
Припустимо, що
необмежена на
.
Проведемо розбиття
відрізку
і нехай на
![]() функція
не є обмеженою. Запишемо інтегральну
суму у вигляді
функція
не є обмеженою. Запишемо інтегральну
суму у вигляді
 .
.
Те,
що
необмежена на
,
означає, що для будь – якого, досить
великого,
![]() на
знайдеться точка
на
знайдеться точка
![]() така, що
така, що
![]() .
.
Візьмемо
послідовність
![]() .
Тоді для
.
Тоді для

Зрозуміло, що
![]() ,
,
а тому
![]()
і
![]() .
.
Це
означає, що вибором проміжних точок
![]() можливо інтегральну суму зробити за
модулем більшою будь-якого наперед
заданого додатнього числа, а тому
інтегральні суми не будуть мати скінченої
границі, коли
.
За умовою
,
що означає існування скінченої границі.
Одержали протиріччя.
можливо інтегральну суму зробити за
модулем більшою будь-якого наперед
заданого додатнього числа, а тому
інтегральні суми не будуть мати скінченої
границі, коли
.
За умовою
,
що означає існування скінченої границі.
Одержали протиріччя.
Наслідок. Якщо визначена і необмежена на , то вона неінтегруєма за Ріманом на .
Наприклад,

необмежена
на
![]() ,
а тому неінтегруєма на
.
,
а тому неінтегруєма на
.
Наступний приклад показує, що обмежена функція може бути неінтегруємою за Ріманом на .
Приклад 2.1. Нехай

де
![]() множина
раціональних чисел,
множина
раціональних чисел,
 .
.
У
будь-якому відрізку є як раціональні,
так і ірраціональні точки. Виберемо
спочатку всі
![]() ,
а тому
,
а тому
 .
.
Якщо
тепер взяти всі
![]() ,
то
,
то
![]() і
і
 .
.
А тому не існує границі множини інтегральних сум, коли .
Зрозуміло,
що функція
![]() (функція Діріхле) неінтегруєма на
,
але обмежена.
(функція Діріхле) неінтегруєма на
,
але обмежена.
Без
доведення відмітимо достатню умову
існування визначеного інтеграла від
обмеженої функції
:
якщо
така, що для будь-якого
можливо вказати скінчену кількість
інтервалів, які покривають множину
точок розриву цієї функції, і сума довжин
цих інтервалів дорівнює
![]() ,
то функція
інтегруєма на
,
то функція
інтегруєма на
![]() .
.
Тоді зрозуміло, що:
Обмежена і неперервна функція всюди на за виключенням скінченої кількості точок (точок розриву), інтегруєма на .
Обмежена і монотонна функція інтегруєма на .
Якщо обмежені функції та
 такі, що
такі, що
 ,
за виключенням скінченої кількості
точок, і функція
,
то
,
за виключенням скінченої кількості
точок, і функція
,
то
 і
і
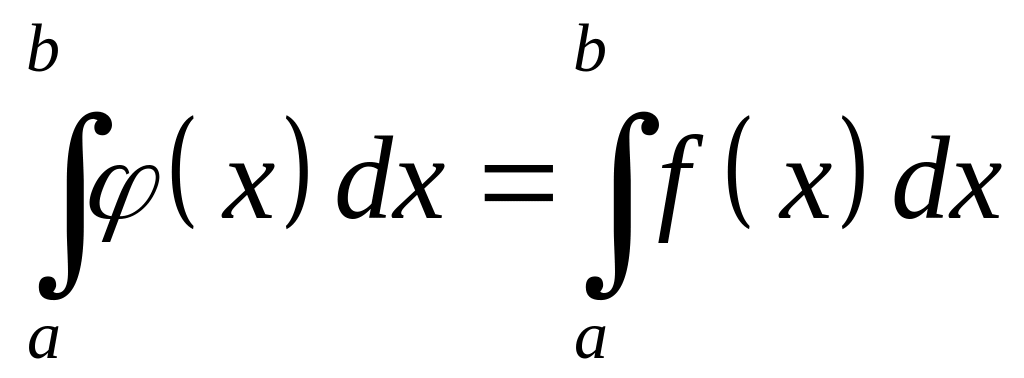 .
.
Приклад 2.2.

Функція
![]() .
.
Приклад 2.3. Функція

інтегруєма
на
![]() .
Точки розриву цієї функції
.
Точки розриву цієї функції
![]()
Для
будь-якого
на
![]() існує нескінчена кількість точок
розриву, а зовні його
скінчена, нехай їх кількість дорівнює
існує нескінчена кількість точок
розриву, а зовні його
скінчена, нехай їх кількість дорівнює
![]() .
Кожну з них можна накрити інтервалом
довжиною
.
Кожну з них можна накрити інтервалом
довжиною
![]() ,
а тому всі точки розриву на
можна накрити інтервалами, сума довжин
яких
,
а тому всі точки розриву на
можна накрити інтервалами, сума довжин
яких
![]() .
.
