
- •I. Линейная алгебра Лекция № 1. § 1. Матрицы.
- •Линейные операции над матрицами. Сложение матриц
- •Разность матриц
- •Произведение матрицы на число
- •Произведение матриц
- •Лекция № 2. § 2. Определители. Определитель второго порядка
- •Свойства определителя второго порядка
- •Определитель третьего порядка
- •Вычисление определителя третьего порядка.
- •Определители высших порядков
- •Системы линейных алгебраических уравнений (слау). Лекция № 3. Слау. Решение систем линейных уравнений методом Крамера.
- •Решение систем линейных уравнений методом Крамера.
- •Теорема. (Правило Крамера):
- •Система трех линейных уравнений с тремя неизвестными.
- •Лекция № 4. Метод Гаусса. Решение систем линейных уравнений методом Гаусса.
- •Лекция № 5. Обратная матрица. Матричный способ решения систем. Обратная матрица
- •Матричный способ решения систем
Системы линейных алгебраических уравнений (слау). Лекция № 3. Слау. Решение систем линейных уравнений методом Крамера.
Определение: Системой линейных алгебраических уравнений, содержащей m-линейных уравнений c n-неизвестными, называется система вида
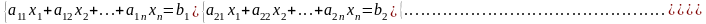 (1),
(1),
Где
числа
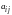 ,
,
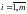 ,
,
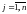 называются коэффициентами системы,
числа
-свободными членами.
называются коэффициентами системы,
числа
-свободными членами.
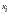 - неизвестные.
- неизвестные.
Обозначим:
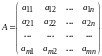 -
матрица системы (основная матрица),
-
матрица системы (основная матрица),
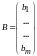 -
матрица сводных членов,
-
матрица сводных членов,
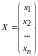 -
матрица неизвестных.
-
матрица неизвестных.
Тогда, пользуясь правилами умножения матриц, система записывается в матричном виде:
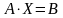 (2)
(2)
Определение:
Матрица, полученная из матрицы
А, присоединением столбца свободных
членов, называется расширенной
матрицей системы линейных уравнений.
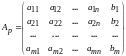 или
или
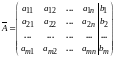 .
.
Определение:
Решением системы
называется набор значений неизвестных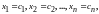 ,
при подстановке которых в систему (1)
все уравнения системы обращаются в
верные числовые равенства. Всякое
решение системы можно записать в виде
матрицы – столбца
,
при подстановке которых в систему (1)
все уравнения системы обращаются в
верные числовые равенства. Всякое
решение системы можно записать в виде
матрицы – столбца
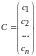 .
.
Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.
Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением.
Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.
Определение: Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение.
Определение: Система линейных уравнений называется однородной, если свободные члены равны нулю.
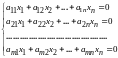
Однородная система всегда совместна, т.к. всегда имеет нулевое решение.
Решение систем линейных уравнений методом Крамера.
Рассмотрим систему n - линейных уравнений с n неизвестными
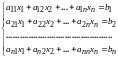 .
.
Теорема. (Правило Крамера):
Теорема. Если определитель матрицы системы из n – линейных уравнений с n неизвестными
не равен нулю
 ,
то система имеет единственное решение
и это решение находится по формуле:
,
то система имеет единственное решение
и это решение находится по формуле:
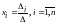 ,
где
,
где
 - определитель
матрицы системы, составленный из
коэффициентов при неизвестных, а
- определитель
матрицы системы, составленный из
коэффициентов при неизвестных, а
 -
определитель матрицы, получаемой из
матрицы системы заменой i-го
столбца столбцом свободных членов
-
определитель матрицы, получаемой из
матрицы системы заменой i-го
столбца столбцом свободных членов
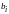 .
.
- формула Крамера.
Система трех линейных уравнений с тремя неизвестными.
Система трех
линейных уравнений с тремя неизвестными
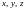 :
:
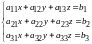 (1).
(1).
Система (1)
неоднородная, если хотя бы один
из свободных членов
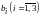 ,
отличен от нуля.
,
отличен от нуля.
Определение: Определитель, составленный из коэффициентов при неизвестных системы, называется главным определителем системы:
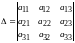 - главный определитель
системы. (2)
- главный определитель
системы. (2)
Определители
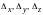 получаются из главного определителя
системы
получаются из главного определителя
системы
 ,
если в нем заменить соответственно
коэффициенты при x, y
и z свободными членами
,
если в нем заменить соответственно
коэффициенты при x, y
и z свободными членами
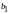 ,
,
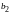 ,
,
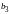 .
.
 (3)
(3)
Решение системы (1) определяется формулами:
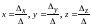 - формулы Крамера.
(4)
- формулы Крамера.
(4)
Система (1) имеет единственное решение, определяемое формулами (4).
Замечание.
Система уравнений называется совместной и определенной, когда она имеет решение, и притом единственное.
Если , то система уравнений решение, и притом единственное,.
Если
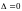 ,
а хотя бы один из определителей
не равен нулю, то система (1) решений не
имеет (т. е. несовместна).
,
а хотя бы один из определителей
не равен нулю, то система (1) решений не
имеет (т. е. несовместна).
Система (1) также может совсем не иметь решений; но если система (1) при этих условиях имеет хотя бы одно решение, то она имеет бесконечно много различных решений.
Замечание.
Совместная система
является неопределенной, если допускает
бесчисленное множество решений. Случай,
когда
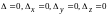 .
.
Система (5) – однородная (все свободные члены равны нулю):
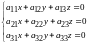 .
(5)
.
(5)
Если
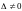 ,
а
,
а
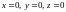 ,
то система имеет единственное решение.
,
то система имеет единственное решение.
Если , система помимо нулевого решения имеет бесконечно много ненулевых решений.
Задачи
Задача
1. Решить систему
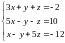 .
.
Решение
Здесь
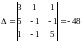 .
.
Так как , система имеет решение, и притом единственное.
Найдем :
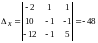 ,
,
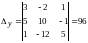 ,
,
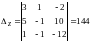 .
.
Тогда по формулам
(4) определяем решение системы
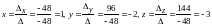 .
.
Ответ: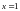 ;
;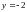 ;
;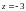 .
.
Задача
2. Решить систему
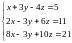 .
.
Решение
Здесь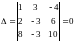 .
.
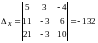
Так как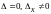 ,
то система несовместна.
,
то система несовместна.
Задача
3. Решить систему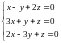 .
.
Решение
Здесь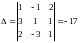 .
Так как
и система однородная, то система имеет
единственное решение
.
Так как
и система однородная, то система имеет
единственное решение
 ,
,
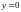 ,
,
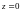 .
.
