
- •17.5. Віддаль від точки до площини
- •§18. Пряма в просторі
- •18.1. Загальне рівняння прямої
- •18.2. Канонічне рівняння прямої
- •18.3. Рівняння прямої, що проходить через дві задані точки
- •18.4. Кут між двома прямими
- •18.5. Взаємне розміщення прямої і площини
- •§19. Криві другого порядку
- •19.1. Коло і його рівняння
- •19.2. Еліпс і його рівняння
- •19.3. Гіпербола та її рівняння
- •19.4. Асимптоти гіперболи
- •19.5. Парабола та її рівняння
- •§ 20. Перетворення прямокутних координат
- •20.1. Перенесення початку координат
- •20.2. Поворот осей координат
- •§21. Полярна система координат
п очатку
координат. Якщо через
очатку
координат. Якщо через
![]() позначимо одиничний вектор нормалі
позначимо одиничний вектор нормалі
![]() ,
то координати
будуть (cosα,cosβ,cosγ).
На основі §8 їх називають направляючими
косинусами нормального вектора. Візьмемо
довільну точку
,
то координати
будуть (cosα,cosβ,cosγ).
На основі §8 їх називають направляючими
косинусами нормального вектора. Візьмемо
довільну точку
![]() на площині
на площині
![]() і позначимо радіус - вектор
і позначимо радіус - вектор
![]() через
через
![]() .
Тоді
.
Тоді
![]() .
Тепер на основі формули (2.15) маємо
.
Тепер на основі формули (2.15) маємо
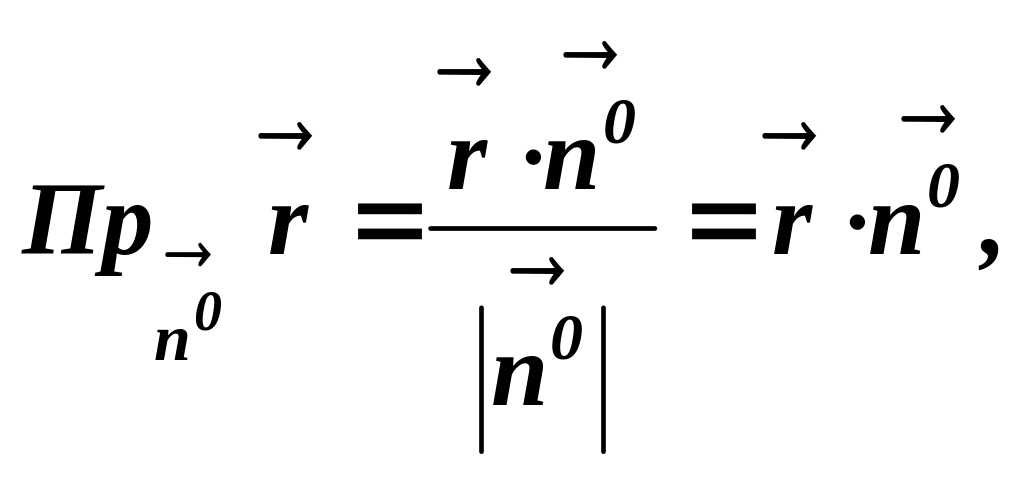
бо
![]() Значить, ми одержимо, що
Значить, ми одержимо, що
![]() або
або
![]() .
(2.81)
.
(2.81)
Рівняння
(2.81) називається нормальним рівнянням
площини у векторній формі. Розпишемо
рівняння (2.81) у координатній формі,
одержимо
![]() .
(2.82).
.
(2.82).
В
цьому рівнянні
![]() віддаль від площини до початку координат
і
віддаль від площини до початку координат
і
![]() .
(2.83)
.
(2.83)
Щоб
загальне рівняння площини привести до
нормального вигляду, потрібно загальне
рівняння площини помножити на сталий
множник
![]() . Одержимо
. Одержимо
![]() , де
, де
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
Піднісши перші три рівності до квадрату і додавши їх, враховуючи (2.83), одержимо
![]() ,
або
,
або
![]() .
(2.84)
.
(2.84)
В формулі (2.84) необхідно брати знак протилежний знаку вільного члена в загальному рівнянні площини, так як , де - завжди додатне як віддаль.
Отже, щоб рівняння (2.72) привести до нормального вигляду , треба помножити його на нормувальний множник (2.84).
17.5. Віддаль від точки до площини
Н ехай
задано нормальне рівняння площини
:
і точка
ехай
задано нормальне рівняння площини
:
і точка
![]() поза площиною. Потрібно обчислити
віддаль від точки
поза площиною. Потрібно обчислити
віддаль від точки
![]() до площини
. (мал. 2.46).
до площини
. (мал. 2.46).
Розв’язування.
Проведемо через точку
площину
![]() паралельну до площини
(мал. 46). Нормальне рівняння площини
запишемо так
паралельну до площини
(мал. 46). Нормальне рівняння площини
запишемо так
![]() де
де
![]() віддаль площини
від початку координат. Шукана віддаль
дорівнює
віддаль площини
від початку координат. Шукана віддаль
дорівнює
![]() .
Тому що точка
.
Тому що точка
![]() знаходиться на площині
,
то
знаходиться на площині
,
то
![]() і значить
і значить
![]() .
Взагалі
.
Взагалі
![]() (2.85)
(2.85)
або
![]() .
(2.86)
.
(2.86)
§18. Пряма в просторі
В просторі, так як і на площині, одну і ту ж пряму можна задати різними по формі рівняннями.
18.1. Загальне рівняння прямої
Пряму
![]() в просторі можна розглядати як лінію
перетину двох площин
і
в просторі можна розглядати як лінію
перетину двох площин
і
![]() (мал.47). Тому загальним рівнянням прямої
є система двох рівнянь першого степеня
, а саме
(мал.47). Тому загальним рівнянням прямої
є система двох рівнянь першого степеня
, а саме
![]()
 (2.87)
(2.87)
Координати
прямої
будуть задовольняти обом рівнянням
системи (2.87). Система (2.87) визначає пряму
лінію
при умові, що нормальні вектори
![]() і
і
![]() неколінеарні, бо тільки в цьому випадку
площини перетинаються.
неколінеарні, бо тільки в цьому випадку
площини перетинаються.
18.2. Канонічне рівняння прямої
П оложення
прямої лінії в просторі визначається
однозначно, якщо відома точка
M0(x0
y0
z0,)
,через яку вона проходить , і відомо
напрямний вектор
оложення
прямої лінії в просторі визначається
однозначно, якщо відома точка
M0(x0
y0
z0,)
,через яку вона проходить , і відомо
напрямний вектор
![]() ,
якому пряма
паралельна (мал.48). Візьмемо на прямій
довільну точку
,
якому пряма
паралельна (мал.48). Візьмемо на прямій
довільну точку
![]() і позначимо
через
,
а вектор
і позначимо
через
,
а вектор
![]() через
через
![]() З малюнка (48) видно , що
З малюнка (48) видно , що
![]() ,
,
або
![]() .
(2.88)
.
(2.88)
Вектор
![]() колінеарний із направляючим вектором
колінеарний із направляючим вектором
![]() ,
тому
,
тому
![]() ,
(2.89)
,
(2.89)
де
![]() -
числовий параметр. Тоді (2.88) запишемо у
вигляді
-
числовий параметр. Тоді (2.88) запишемо у
вигляді
![]() .
(2.90)
.
(2.90)
Рівняння (2.90) називається векторним рівнянням прямої в просторі. Розпишемо рівняння (2.90) в координатній формі
![]() .
(2.91)
.
(2.91)
Рівняння
(2.91) називаються параметричними рівняннями
прямої. Якщо параметр
змінюється, то точка
рухається по прямій
![]()
Виключивши параметр із рівнянь (2.91) , одержимо
![]() Звідси
Звідси
![]() .
(2.92)
.
(2.92)
Рівняння
(2.92) називаються канонічними рівняннями
прямої в просторі, а координати
![]() і
вектора
-
направляючими коефіцієнтами прямої.
і
вектора
-
направляючими коефіцієнтами прямої.
В
канонічних рівняннях (2.92) величини
і
не можуть одночасно перетворюватися в
нуль, так як
![]() ,
але деякі із них можуть дорівнювати
нулю.
,
але деякі із них можуть дорівнювати
нулю.
Нехай,
наприклад,
![]() ,
то із рівнянь (2.91) одержимо таку систему
,
то із рівнянь (2.91) одержимо таку систему
 (2.93)
(2.93)
Кожне із цих двох рівнянь визначає площину, а система рівнянь (2.92) визначає пряму. В цьому випадку рівняння (2.92) можна записати умовно так:
![]() .
(2.94)
.
(2.94)
Система
рівнянь (2.93) або (2.94) визначає пряму, яка
перпендикулярна до вісі
![]() ,
так як
.
Якщо які-небудь два направляючих
коефіцієнти рівні нулю, наприклад,
m=0,n=0,
p≠0,
то із рівняння (2.91) одержимо, що
,
так як
.
Якщо які-небудь два направляючих
коефіцієнти рівні нулю, наприклад,
m=0,n=0,
p≠0,
то із рівняння (2.91) одержимо, що
![]() (2.95)
(2.95)
Рівняння (2.92) умовно запишеться так:
![]() .
(2.96)
.
(2.96)
Пряма,
яка визначається системою (2.95), або
(2.96) паралельна осі
![]() і перпендикулярна до осей
і
і перпендикулярна до осей
і
![]() .
.
Канонічні рівняння прямої (2.92) можна представити як сукупність двох рівнянь, наприклад
![]() і
і
![]() .
(2.97)
.
(2.97)
Кожне
із цих рівнянь представляє площину.
Перша площина паралельна вісі
,
так як в рівнянні відсутня координата
![]() ,
а друга паралельна осі
.
,
а друга паралельна осі
.
Таким чином, пряму можна розглядати як перетин двох площин, тобто канонічні рівняння прямої (2.92) записали у загальному вигляді прямої (2.97).
