Примітка. При доведенні даної теореми використали транспонування добутку матриць за формулою

Зауважимо, що в канонічній формі (2.48) є власними числами матриці .

Приклад 2. Привести квадратичну форму до канонічного вигляду з допомогою ортогональної матриці і знайти її.

Розв’язування. Матриця даної квадратичної форми має вигляд . Запишемо систему типу (2.39) для знаходження власних чисел і власних векторів

(2.49)

Характеристичне рівняння даної системи має вигляд

або

Розв’язавши дане рівняння знаходимо

Значить канонічний вигляд даної квадратичної форми є .

Знайдемо ортогональну матрицю.

Стовпчиками ортогональної матриці, яка приводить квадратичну форму до канонічного вигляду є ортонормовані власні вектор-стовпчики матриці

Спочатку знайдемо нормований власний вектор-стовпчик матриці з власним значенням Для цього із системи (2.49) маємо систему для знаходження координат вектора

Із даної системи знаходимо або .

Значить при довільному , відмінному від нуля, стовпчик є власним вектором-стовпчиком матриці а стовпець є нормованим власним вектором-стовпчиком матриці (Тут використано, що 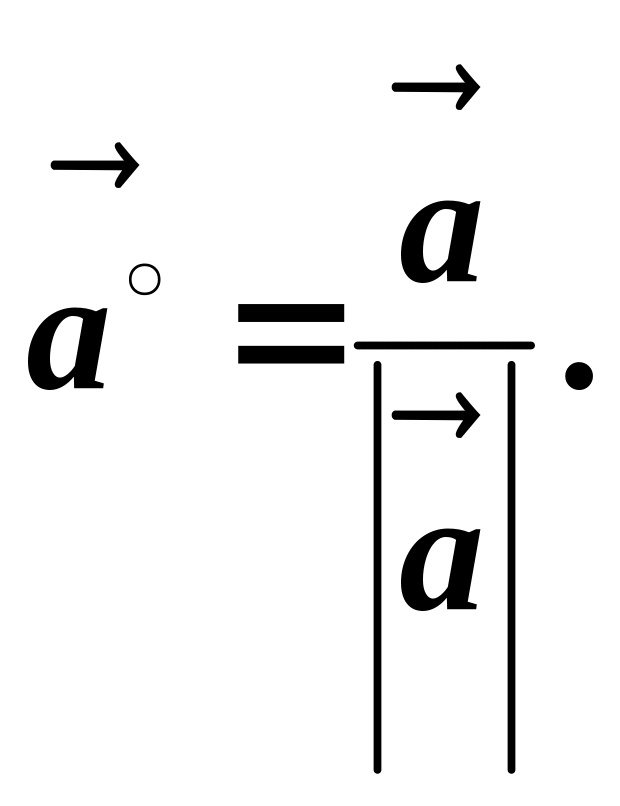Аналогічно знаходимо вектор-стовпчик матриці з власним значенням , а саме із системи:

Знаходимо або при довільному , яке відмінне від нуля, стовпчик є власним вектором матриці Стовпчик є нормованим власним вектором матриці Значить шукана матриця має вигляд

Зауваження.Легко перевірити, що для даного приклада 2.

Розглянемо на прикладі ще один метод приведення квадратичної форми до канонічного вигляду.

Метод Лагранжа приведення квадратичної форми до канонічного вигляду заключається в послідовному виділенні повних квадратів.

Приклад 3. Привести до канонічного вигляду квадратичну форму методом Лагранжа. Спочатку виділимо повний квадрат при змінній , коефіцієнт при якій відмінний від нуля.

І так, невироджене лінійне перетворення

приводить дану канонічну форму до канонічного вигляду

Канонічний вигляд квадратичної форми не є однозначним, так як одна й та ж квадратична форма може бути приведена до канонічного вигляду багатьма способами. Однак одержані різними способами квадратичні форми мають ряд спільних властивостей.

Сформулюємо одну із цих властивостей, яка виражає закон інерції квадратичних форм, що заключається в наступному: всі канонічні форми, до яких приводиться дана квадратична форма, мають:

1. одне й те ж число нульових коефіцієнтів;

2. одне й те ж число додатніх коефіцієнів;

3. одне й те ж число від’ємних коефіцієнтів.

Означення1.Квадратична форма називається додатньо визначеною, якщо для всіх дійсних значень використовується нерівність .

Означення 2. Якщо є додатньо визначеною формою, то квадратична форма називається від’ємно визначеною.

Необхідні та достатні умови додатньої (від’ємної) визначеності квадратичної форми дає наступна теорема.

ТЕОРЕМА 2. Для того, щоб квадратична форма була додатньо (від’ємно) визначеною, необхідно й досить, щоб всі власні значення ( матриці були додатніми(від’ємними).

Дану теорему приводимо без доведення.

В багатьох випадках для встановлення знаковизначеності квадратичної форми зручно застосовувати критерії Сільвестра.

ТЕОРЕМА 3.Для того,щоб квадратична форма була додатньо визначеною, необхідно і досить, щоб всі головні мінори матриці цієї форми були додатніми, тобто

, де , …

Слід зауважити, що для від’ємно визначених квадратичних форм знаки головних мінорів чергуються, починаючи з знаку “мінус” для мінора першого порядку.

Наприклад, квадратична форма L в прикладі 2 є додатньо визначеною на основі теореми 2, так як корені характеристичного рівняння λ₁=6 і λ₂=1 є додатніми.

Другий спосіб. Так як головні мінори матриці A.

є додатніми, то за критерієм Сільвестра дана квадратична форма є додатньо визначеною.

§16. Пряма лінія на площині

Рівняння лінії є важливим поняттям аналітичної геометрії. Нехай на площині ми маємо деяку лінію (криву) (мал.22).

О значення. Рівнянням лінії (кривої) на площині називається рівняння, якому задовольняють координати і кожної точки, що знаходиться на цій лінії і не задовольняють координати іншої точки, що не знаходиться на цій лінії.

В загальному випадку рівняння лінії будемо записувати у вигляді F(x,y)=0 або y=f(x) Якщо точка M(x,y) рухається по лінії, то її координати змінюються і тому ці координати називаються біжучими.

16.1. Рівняння прямої з кутовим коефіцієнтом.

Нехай пряма l (мал.23) перетинає вісь ординат в точці

A(0,b) і утворює з додатнім напрямом вісі Ox кут φ (0< φ< ).

В ізьмемо на прямій довільну точку З точки проведемо пряму паралельну до перетину з відрізком Позначимо через -кутовий коефіцієнт. Таким чином, величини і повністю визначають положення прямої на площині. Знайдемо рівняння прямої за заданими параметрами і . Іншими словами покажемо, яким рівнянням пов’язані координати довільної точки прямої. З прямокутного трикутника знаходимо

. (2.50)

З рівності (2.50), вважаючи , одержимо

. (2.51)

Рівняння (2.51) називається рівнянням прямої з кутовим коефіцієнтом.

М ожна легко довести, що формула (2.51) також справедлива для випадку, коли

Значить, координати довільної точки прямої задовольняють рівнянню (2.51).

Розглянемо частинні

випадки рівняння .

а) Якщо , то одержимо -рівняння прямої , що проходить через початок координат (мал.24). Коли , то кут - гострий, а коли , то кут тупий.

б ) Якщо і рівняння прямої, паралельної вісі , має вигляд , а рівняння вісі буде (мал.25).

в ) Якщо то не існує і пряма перпендикулярна вісі тобто вертикальна пряма не має кутового коефіцієнта. Нехай ця пряма відсікає на вісі відрізок, що дорівнює (мал.26). Тоді рівняння її буде , а рівняння вісі буде

16.2.Рівняння прямої, що проходить через задану точку в даному напрямку

Нехай задана точка і потрібно написати ріваняння прямої лінії, що проходить через цю точку.

Н ехай пряма , що проходить через точку , утворює з віссю кут (мал.27).

Тому що точка знаходиться на прямій, то її координати задовольняють рівнянню (2.51), тобто

. (2.52)

Віднімаючи рівняння (2.52) від (2.51), одержимо рівняння шуканої прямої

. (2.53)

Рівняння (2.53) звуть в’язкою прямих, де - довільне число. Через точку проходить безліч прямих, крім прямої, паралельної вісі

16.3.Рівняння прямої, що проходить через дві задані точки

Н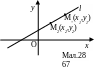 ехай задано дві точки і .

Для одержання рівняння прямої (мал.28) запишемо рівняння прямої, що проходить через точку

, а саме .

Оскільки точка знаходиться на прямій , то підставивши координати цієї точки в рівняння в’язки прямих(2.53), одержимо . З цієї рівності знайдемо кутовий коефіцієнт прямої

(2.54)

Тепер підставивши вираз для , тобто (2.54) в рівняння (2.53) і одержимо шукане рівняння прямої

(2.55)

Примітка. Якщо точки і лежать на прямій , яка паралельна осі , тобто , то рівняння прямої буде . Коли згадані точки лежать на прямій, яка паралельна вісі , тоді і рівняння прямої буде

Приклад 1. Скласти рівняння прямої, що проходить через точки і

Розв’язування. Використовуючи формулу (2.55), запишемо

або .

Розкривши пропорцію, маємо . Спростивши, одержимо .

16.4. Рівняння прямої у відрізках

Нехай пряма відсікає від початку координат на осі відрізок , а на осі відрізок , тоді пряма проходить через дві точки і .

В икориставши формулу (2.55) для точок і , одержимо і після спрощення маємо

. (2.56)

Рівняння (2.56) називається рівнянням прямої у відрізках.

Приклад 2. Скласти рівняння прямої, що проходить через точку A(1;2), яка відтинає на додатній осі відрізок у два рази більший як на додатній осі

Розв’язування.У рівності (2.56) за умовою Підставляючи координати точки A(1;2) і у рівняння (2.56), одержимо , або і

Тоді рівняння шуканої прямої буде .

16.5. Кут між двома прямими

Н ехай задано дві прямі і :

,

,

і потрібно знайти кут між ними (мал.40).

Із мал.40 видно, що , причому , , , .

Тоді

або (2.57)

де стрілка на мал. 40 означає, що кут береться проти годинникової стрілки від до .

Формула (2.57) є формула для знаходження кута між двома прямими.

Якщо l₁l₂ то і . Тоді із формули (2.57) маємо, що

(2.58)

Умова (2.58) є необхідною і достатньою умовою паралельності двох прямих.

Якщо то тоді і не існує. Перейдемо до

Тепер формула (2.57) запишеться так

і коли , то . Одержимо умову перпендикулярності двох прямих:

(2.59)

Висновок. Прямі і паралельні тоді і тільки тоді, коли їх кутові коефіцієнти рівні і ці прямі перпендикулярні, коли добуток їх кутових коефіцієнтів дорівнює “–1”.

Приклад 3. Знайти кут між прямими і

Розв’язування. Знаходимо і . Підставивши значення цих кутових коефіцієнтів у формулу (2.57), одержимо

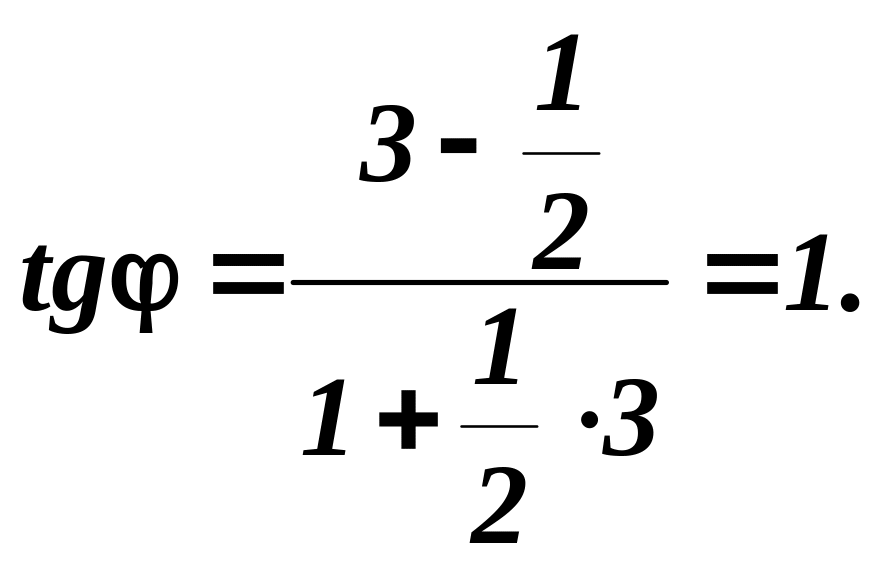
Звідси знаходимо .

Приклад 4. Затрати перевезень двома засобами транспорту виражаються функціями і , де - віддаль перевезень в сотнях кілометрів, а - транспортні витрати. Починаючи з якої віддалі , найбільш економічним є другий засіб транспорту?

Р озв’язування. Намалюємо графіки заданих функцій і побачимо, що вони перетинаються в точці (5;200). Щоб перевірити даний результат, розв’яжемо систему рівнянь

,

або ,

З даного малюнка видно, що при віддалі, яка перевищує 500 км найбільш економічним є другий засіб транспорту.

16.6. Загальне рівняння прямої та його дослідження.

Н ехай задана точка через яку проходить пряма і вектор , який перепендикулярний до прямої (мал.41). На прямій беремо довільну точку . Тому що вектор є перепендикулярним до вектора , то скалярний добуток цих векторів дорівнює нулю, тобто

. (2.60)

Рівняння (2.60) є векторне рівняння прямої . Розпишемо це рівняння в координатній формі. Оскільки то рівняння (2.60) перепишеться у вигляді

Розкривши дужки, одержимо

, (2.61)

де .

Рівняння (2.61) називається загальним рівнянням прямої. Дослідимо як розміщена пряма, що задана рівнянням (2.61), якщо деякі коефіцієнти і будуть рівні нулю.

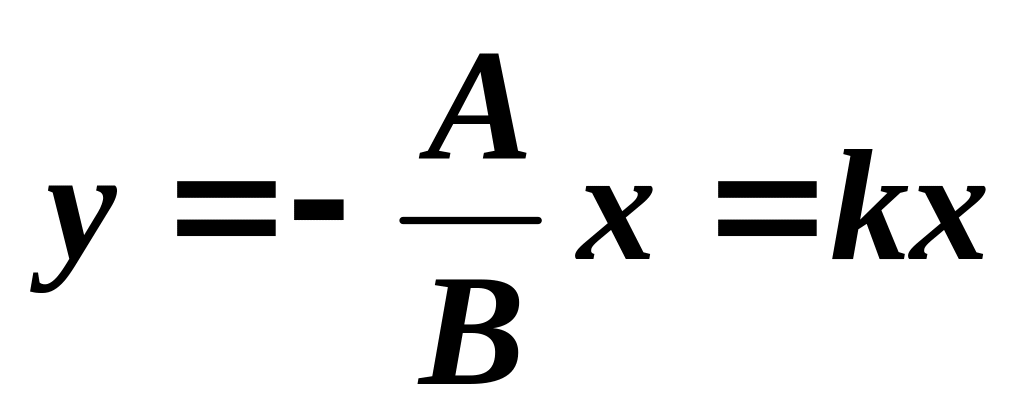1. Якщо , то рівняння (2.61) має вигляд або , де

Значить, якщо вільний член , а саме , то пряма проходить через початок координат.

2. Якщо , то рівняння прийме вигляд або , тобто пряма паралельна осі

3. Якщо , то рівняння (2.61) має вигляд або є рівнянням прямої, паралельної осі ординат.

4. Якщо , то рівняння прийме вигляд , звідси Це і є рівняння осі

5. Якщо , то рівняння (2.61) буде мати вигляд 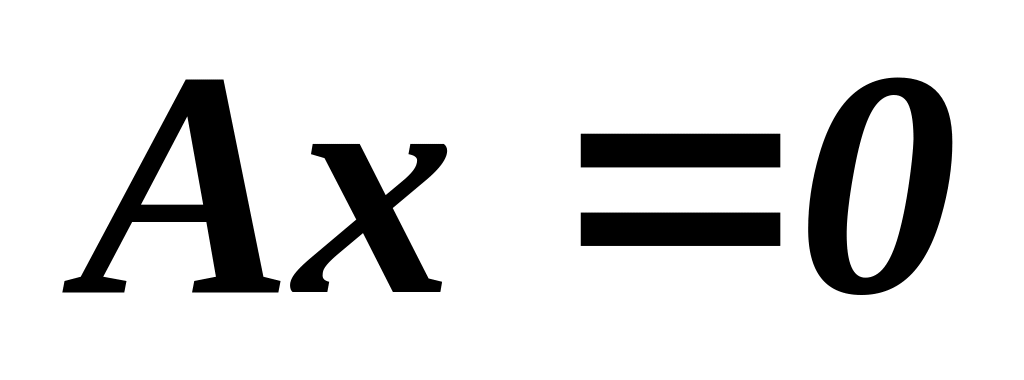або . Це рівняння осі

Якщо задані дві прямі і загальними рівняннями

, ,

, .

то щоб знайти координати точки перетину цих прямих, які повинні задовольняти рівняння кожної прямої, то потрібно розв’язати систему рівнянь

Якщо прямі і паралельні, то їх кутові коефіцієнти і рівні. Отже, або .

Значить, умова паралельності прямих, які задані загальними рівняннями, є пропорціональність коефіцієнтів при невідомих.

Умова перпендикулярності прямих в цьому випадку має вигляд або .

Отже, для прямих які задані загальними рівняннями, умовою перпендикулярності є рівність нулю суми добутків коефіцієнтів при змінних і .

16.7. Нормальне рівняння прямої

Нехай положення прямої на площині визначається двома

величинами (параметрами прямої) : довжиною і напрямком

перпендикуляра ОР, опущеного із початку координат на пряму і величиною кута , який утворює даний перпендикуляр з віссю (мал.42).

Н а прямій візьмемо довільну точку . Позначимо довжину перпендикуляра через , а орт нормалі через . Проекція радіус-вектора на нормаль буде завжди рівною .

Таким чином, пряма визначається як геометричне місце точок площини, проекції радіус-векторів яких на нормаль дорівнює сталій величині .

На основі скалярного добутку маємо

. (2.62)

Рівняння (2.62) є нормальним рівнянням прямої у векторній формі.

Тому що , координати , вектор то в координатній формі рівняння (2.62) буде мати вигляд

. (2.63)

Якщо пряма лінія задана загальним рівнянням

то це рівняння можна звести до нормального рівняння прямої (2.63).Помножимо загальне рівняння прямої на деякий множник

(2.64)

Одержане рівняння і загальне рівняння прямої рівносильні. Щоб рівняння (2.64) було нормальним, тобто мало вигляд (2.63) потрібно, щоб виконувалися рівності

(2.65)

Перші дві рівності в (2.65) піднесемо до квадрату і додамо. Тоді одержимо, що

, (2.66)

називається нормувальним множником.

Третя рівність (2.65) встановлює знак множника , а саме знак є протилежним знакові вільного члена

Приклад 4. Привести до нормального вигляду рівняння

Розв’язування. Знаходимо нормувальний множник

(вибираємо знак плюс, так як

Помноживши на дане рівняння, одержимо

Одержане рівняння і є нормальним рівнянням прямої. В цьому рівнянні .

16.8. Віддаль від точки до прямої

Нехай маємо пряму l, задану рівнянням і точку М₀ (х₀,у₀) Потрібно знайти віддаль від цієї точки до прямої l.

Через точку проведемо пряму паралельну прямій

Шукану віддаль від точки до прямої позначимо через Тому що а , то

Якщо б точка знаходилася на тій же віддалі від прямої , але з другого боку, то тоді

Таким чином, шукана віддаль визначається рівністю

або .

Нормальне рівняння прямої паралельної має вигляд

. (2.67)

Т ому що точка знаходиться на прямій , то її координати задовольняють рівнянню (2.67), тобто

і звідси .

Підставляючи значення в рівність , одержимо (2.68)

Формула (2.68) є формулою віддалі від точки до прямої, заданої нормальним рівнянням.

Якщо ж пряма задана загальним рівнянням, то віддаль від точки знаходиться за формулою

. (2.69)

Приклад. Знайти віддаль від точки до прямої

Розв’язування. Тепер підставляємо замість і координати точки , тобто в формулу (2.69) і знаходимо шукану віддаль