ПТЦА Лекция____ Лист____

ФОРМАТЫ ПРЕДСТАВЛЕНИЯ ДАННЫХ В ЭВМ

Рассмотреть:

1. Фиксированная точка.

2. Плавающая точка.

3. Упакованный и зонный формат.

4. Представление алфавитно-цифровой информации.

ВЫПОЛНЕНИЕ ОПЕРАЦИЙ АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ И СДВИГА В ЭВМ

Важнейшей функцией большинства вычислительных устройств является выполнение арифметических и логических операций. Для этого в ЭВМ вводят специальные функциональные блоки (один, а в современных процессорах несколько) арифметическо-логических устройств (АЛУ).

Основной операцией в ЭВМ является операция сложения. По способу ее выполнения АЛУ могут быть параллельного, последовательного и параллельно-последовательного действия.

При вычислении суммы двух чисел возможны два случая:

• слагаемые имеют одинаковые знаки;

• слагаемые имеют разные знаки.

В соответствии с этим алгоритмы получения суммы для каждого из вариантов значительно отличаются между собой.

Так, алгоритм получения суммы двух чисел с одинаковыми знаками может быть представлен следующим образом:

1. Сложить два числа.

2. Сумме присвоить знак одного из слагаемых.

В то же время алгоритм получения алгебраической суммы может быть представлен следующим образом:

1. Сравнить знаки слагаемых и, если они одинаковы, то выполнить сложение по предыдущему алгоритму.

2. Сравнить слагаемые по абсолютной величине, если знаки слагаемых разные.

3. Если есть необходимость, переставить числа местами (чтобы вычитать из большего меньшее).

4. Произвести вычитание двух чисел.

Из этого следует, что первый алгоритм значительно проще второго. Следовательно, желательно преобразовать отрицательные числа таким образом, чтобы операцию вычитания заменить сложением, т.е. выполнять суммирование двух чисел следующим образом: S = A + (- B)

Для этого необходимо изобразить положительные и отрицательные числа единым натуральным кодом, что возможно достичь единственным образом при использовании систем счисления с положительным основанием и симметричной базой либо с отрицательным основанием и неотрицательной базой.

При использовании однородных позиционных систем счисления с положительным основанием и неотрицательной базой натуральным кодом можно представить только положительные числа и нуль (т.е. в этом случае нет единого натурального кода для положительных и отрицательных чисел). Это приводит к тому, что проблему представления чисел со знаком приходится решать при помощи специальных кодов: прямого, обратного и дополнительного.

1. Прямой код

Прямым кодом отрицательного двоичного числа называется его изображение в естественной форме записи, у которой в знаковом разряде ставится единица. Прямой код положительного двоичного числа совпадает с его обычным изображением в естественной форме, т.к. знак кодируется нулем.

Правила сложения чисел в прямом коде не отличаются от обычных правил сложения, т.е. если оба слагаемых имеют одинаковые знаки, то их числовые разряды складываются, а сумме приписывается знак одного из них. Если слагаемые имеют разные знаки, то из числовых разрядов большего по абсолютной величине числа вычитается меньшее, а сумме приписывается знак большего слагаемого. При этом числовые разряды кода обрабатываются отдельно от знаковых разрядов, так как последние не имеют веса.

Рассмотреть 4 случая получения суммы при | A | > | B | и | A | + | B | < 1.

| A |= 0.10110; | B | = 0.00101

1. А > 0; B > 0; C > 0;

2. А > 0; B < 0; C > 0;

3. А < 0; B > 0; C < 0;

4. А > 0; B < 0; C < 0.

Таким образом, в прямом коде знаковый разряд и цифровую часть числа нельзя рассматривать как единое целое, а выполнение операции сложения затруднено тем, что необходимо кроме сумматора иметь в составе АЛУ и вычитатель кодов чисел. Эти недостатки настолько серьезны, что прямой код для выполнения операций алгебраического сложения не применяется, но он удобен для операций умножения и деления.

2. Дополнительный код

Замена операции вычитания операцией сложения основана на применении некоторых вспомогательных положительных чисел, однозначно связанных с исходными отрицательными числами, в связи с чем эти вспомогательные числа можно считать исходными, но некоторым образом закодированными.

Эти числа находятся как дополнение модулей заданных отрицательных операндов до некоторого граничного числ а

Х_гр = | X_max | + 10^-n = 10ⁿ;

n –количество разрядов в целой части.

[X]_доп = Х_гр - | X |.

Пусть 0 ≤ X ≤ X_max = 99

Х_гр = 99 + 1 = 100 = 10².

Пусть Х₁ = 84, Х₂ = - 63.

[X]_доп = 100 – 63 = 37.

Х₁ + [X₂]_доп = 84 + 37 = 121 => 21

Действительно,

Х₁ + [X₂]_доп = 84 + (100 - 63) = 121 – 100 = 21

Д ля нахождения дополнительного кода отрицательного числа вычитание производится из одного и того же числа. Поэтому можно предложить следующий алгоритм.

Сумма взаимообратных цифр равна старшей цифре системы счисления.

Замена в некотором отрицательном числе всех цифр на взаимообратные равносильна сложению исходного числа с максимальным числом в заданном разряде.

Таким образом, для получения дополнения отрицательного числа следует все цифры исходного числа заменить на взаимообратные и к полученному таким образом «обратному числу» добавить единицу младшего разряда.

Следовательно, в ЭВМ с использованием десятичной системы счисления для образования дополнительного кода необходимо иметь в памяти 5 пар взаимообратных цифр.

Для двоичной системы счисления эта процедура гораздо проще. Для целых чисел Х_гр = 2ⁿ, где n – вес несуществующего в данном числе разряда, расположенного слева от знакового разряда. Для дробных чисел граничным числом является 1.

Дополнительный код отрицательного числа это его дополнение до граничного числа.

Для получения дополнительного кода отрицательной двоичной дроби необходимо в ее знаковом разряде записать 1, все цифры исходного числа заменить на инверсные (1 на 0 и 0 на 1) и прибавить единицу младшего разряда к преобразованному числу. Или, что тоже самое, младшую единицу и все нули справа от нее оставить без изменения, а разряды слева от этой единицы заменить на инверсные.

Обратный переход от дополнительного кода к его естественному изображению производится аналогично.

3. Обратный код

При замене операции вычитания операцией сложения можно воспользоваться инверсией отрицательного операнда, получаемой заменой его цифр на взаимообратными.

Обратным кодом отрицательного двоичного числа будем называть его дополнение по модулю до Х_max, получаемое по следующему правилу: в знаковом разряде проставляется 1, а во всех остальных разрядах цифры заменяются н а взаимообратные.

[Х]_{обр. отриц.} = Х + Х_max.

Основное достоинство – простота формирования.

Недостатки:

1. Два изображения 0.

2. Циклический перенос из знакового разряда при сложении, который необходимо прибавить к младшему разряду суммы.

Алгебраическое сложение чисел с фиксированной точкой в ЦВМ производится в одном из машинных кодов - обратном или дополнительном. При этом знаковый разряд и цифровая часть числа рассматриваются как единое целое.

Главное достоинство обратных и дополнительных кодов - правильный знак суммы.

Возможны 4 случая:

X₁>0 X₂>0 X₃= X₁+X₂>0

X₁>0 X₂<0 X₃= X₁+X₂>0 |X₁|>|X₂|

X₁>0 X₂<0 X₃= X₁+X₂<0 |X₁|<|X₂|

X₁<0 X₂<0 X₃= X₁+X₂<0

Пример:

X₁=Зн.10101 X₂=Зн.00101 (Четыре варианта знаков чисел).

(Рассмотреть суммы этих чисел в естественной форме, прямом, обратном, и дополнительных кодах).

Определение переполнения разрядной сетки при сложении. Модифицированные коды

В силу ограниченности разрядной сетки АЛУ при сложении чисел с одинаковыми знаками может возникать ее переполнение – результат не помещается в разрядную сетку. Результат переполняет разрядную сетку если перенос в знаковый разряд присутствует, а перенос из знакового разряда отсутствует (положительное переполнение), или перенос в знаковый разряд отсутствует, а из знакового разряда присутствует (отрицательное переполнение). Наличие или отсутствие одновременно обоих переносов говори о правильности полученного результата, т.е. сумма помещается в разрядную сетку АЛУ.

Для определения такого факта используются модифицированные обратный и дополнительный коды, в которых знак представляется двумя разрядами: знак плюс кодируется «00», минус - «11».

При положительном переполнении знаковые разряды принимают значение «01», при отрицательном переполнении – «10».

Привести примеры.

Особенности сложения чисел, представленных в форме с плавающей запятой

Операция сложения чисел, представленных в форме с плавающей запятой распадается на 4 этапа:

1. Выравниваются порядки слагаемых (меньший порядок увеличивается до большего, а мантисса преобразуемого числа сдвигается вправо (число денормализуется)). В машине определяется Р₁-Р₂, а потом ясно, что и куда сдвигать.

2. Производится преобразование мантисс слагаемых в один из модифицированных кодов.

3. Мантиссы суммируются по правилам сложения дробных чисел с фиксированной запятой.

4. В случае надобности мантисса суммы переводится в прямой код, производится нормализация суммы и округление мантиссы

Преобразовывать всегда нужно меньшее слагаемое, т.е. то у которого порядок меньше, чтобы не произошло переполнения разрядной сетки мантиссы преобразуемого числа. При сложении мантисс может произойти «временное, кажущееся» переполнение разрядной сетки, которое можно устранить путем сдвига мантиссы результата вправо и увеличением порядка результата.

Коме того, при сложении чисел, представленных в форме с плавающей запятой возможны следующие особые случаи, которые вызывают прерывания работы процессора:

• переполнение порядка (выход величины порядка за пределы разрядной сетки в положительную сторону);

• исчезновение порядка (выход величины порядка за пределы разрядной сетки в отрицательную сторону);

• потеря значимости (получение нулевой мантиссы при ненулевом порядке).

Операционный автомат и микропрограмма сложения чисел, представленных в форме с фиксированной запятой

Пусть необходимо построить операционное устройство для выполнения сложения чисел, представленных в форме с фиксированной запятой. Исходные операнды поступают на вход устройства последовательно за два такта по шине DI(0:7) в следующем формате:

Результат должен быть выдан на шину DO(0:7) в таком же формате. В случае переполнения необходимо сформировать сигнал признака переполнения OV.

Тогда структурная схема ОУ будет иметь вид.

Напишем микропрограмму и построим операционный автомат сложения чисел с фиксированной запятой.

Операционное устройство (ОУ) может быть представлено в виде композиции двух автоматов: операционного (ОА) и управляющего (УА) (рис.1).

Для построения ОУ, выполняющего операцию сложения чисел, представленных в форме с фиксированной запятой, необходимо выбрать алгоритм выполнения заданной операции. Как известно, для выполнения арифметических операций над числами в ЭВМ используются прямой, обратный и дополнительные к оды чисел. При этом основную операцию сложения в ОА выполняет сумматор. Наибольшее распространение получили сумматоры обратного и дополнительного кодов. Будем считать, что для выполнения операции сложения будет использоваться комбинационный сумматор чисел, представленных в дополнительном коде. Суммирование будем выполнять в модифицированном дополнительном коде (два разряда для представления знака числа). Для этого в сумматор вводится дополнительный разряд.

Можно предложить следующий алгоритм выполнения операции сложения чисел, представленных в форме с фиксированной запятой.

0. Принять операнды по входной шине на регистры А и В.

1. Перевести операнды в дополнительный модифицированный код.

2. Выполнить сложение полученных кодов операндов на сумматоре дополнительного кода.

3. Проверить на отсутствие переполнения разрядной сетки. Если есть переполнение – установить признак переполнения в 1. Переход на п.6.

4. Перевести результат в прямой код.

5. Выдать результат на выходную шину.

6. Конец.

Микропрограмма содержит исходные данные для построения ОУ. На ее основе можно построить операционный и управляющий автоматы, а, следовательно, и все операционное устройство в целом.

Для построения управляющего автомата строится кодированная ГСА и синтез УА проводится одним из ранее рассмотренных методов.

Для построения ОА используются следующие списки:

1. Список слов и их типов, которые были использованы при написании микропрограммы (ее описательная часть). Он имеет следующий вид.

• РгА(0:7) – внутреннее слово с памятью;

• РгВ(0:7) – внутреннее слово с памятью;

• РгС(0:8) – внутреннее слово с памятью;

• OV – внутреннее и выходное слово с памятью;

• DI(0:7) – входное слово без памяти;

• DO(0:7) – выходное слово без памяти.

2. Список микроопераций.

   • y₁: РгА:= DI;

   • y₂: РгB:= DI;

   • y₃: РгА:= РгА(1:7)+1;

   • y₄: РгB:= РгB(1:7)+1;

   • y₅: РгС:= РгА(0).РгА + РгВ(0).РгВ;

   • y₆: OV := 1;

   • y₇: РгC:= РгC(2:8)+1;

   • y₈: DO:= РгC(1:8).

3. Список логических условий.

• x₁ = РгА(0);

• x₂ = РгB(0);

• x₃ = С(0)  С(1);

• x₄ = РгС(0).

Структурная схема ОА будет иметь следующий вид.

Если разметить ГСА как автомат Мили, то можно сделать вывод, что в зависимости от знаков операндов микропрограмма выполняется от 4 – 7 тактов. Написав другую микропрограмму, можно получить ОУ, выполняющую операцию, сложения за 2 такта (один из которых занимает прием первого слагаемого в ОА).

Также можно предложить различные промежуточные варианты, отличающиеся быстродействием и затратами оборудования.

Умножение чисел с фиксированной точкой.

Существуют 2 основных способа умножения:

1. Умножение, начиная с младших разрядов множителя

2. Умножение, начиная со старших разрядов множителя

Рассмотрим умножение на примере двоичных чисел.

О

0,101

0,101

——

101

000

101

———

0,011001

собенности умножения двоичных чисел в 2-й системе счисления:

1. Каждое частичное произведение представляет собой либо 0 либо множимое, сдвинутое на соответствующее количество разрядов влево или вправо в зависимости от способа умножения.

2. Т.о. умножение в 2-й системе счисления естественным образом сводится к двум операциям: сложению и сдвигу, т.е. для выполнения операции умножения нужен сумматор и сдвигатель (сдвиговый регистр).

3. Количество значащих цифр в произведении равно сумме значащих цифр в обоих сомножителях.

4. Знак произведения определяется как сумма по mod 2 знаковых размеров сомножителей.

Операция умножения состоит из ряда последовательных операций сложения частичных произведений. Операциями сложения управляют разряды множителя: если в очередном разряде множителя есть «1», то к сумме частных произведений добавляется множимое с соответствующим сдвигом; если в разряде множителя «0», то множимое не прибавляется.

В зависимости от того, что сдвигается (множимое или сумма частичных произведений) различают 4 метода реализации умножения.

1. Умножение, начиная с младших разрядов множителя, со сдвигом суммы частичных произведений вправо и при неподвижном множимом.

Р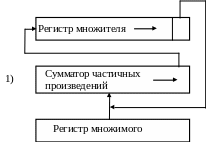 егистр множителя и сумматор частичных произведений при этом должны иметь цепи сдвига вправо. Регистр множимого может не иметь цепей сдвига.

Так как по мере сдвига множителя вправо старшие разряды регистра множителя освобождаются, он может быть использован для хранения младших разрядов произведения, поступающих из младшего разряда сумматора частичных произведений по мере выполнения умножения. После окончания умножения старшие разряды произведения находятся в регистре сумматора, младшие – в регистре множителя.

При данном методе все три регистра имеют одинаковую длину, равную разрядности сомножителей. Этот метод нашел наибольшее применение в ЭВМ.

2. Умножение, начиная с младших разрядов множителя, при сдвиге множимого влево и неподвижной сумме частичных произведений.

Регистр множителя должен иметь цепи сдвига вправо, регистр множимого – цепи сдвига влево.

При этом методе регистр множимого и сумматор частичных произведений должны иметь двойную длину. Метод требует больше оборудования, но никаких преимуществ не дает, поэтому его применение нецелесообразно.

3. Умножение, начиная со старших разрядов множителя, при сдвиге суммы частичных произведений влево и неподвижном множимом.

Р егистр множителя регистр сумматора частичных произведений должны иметь цепи сдвига влево.

При этом методе сумматор частичных произведений должен иметь двойную длину. Метод требует дополнительного по сравнению с первым методом оборудования. Несмотря на это он применяется в некоторых АЛУ, так как позволяет без дополнительных цепей сдвига выполнять и деление. Для выполнения операции деления на оборудовании метода 1 необходимы дополнительные цепи сдвига влево в регистре множимого (частного) и в сумматоре частичных произведений (разностей).

4. Умножение, начиная со старших разрядов множителя, при сдвиге множимого вправо и неподвижной сумме частичных произведений.

Р егистр множителя должен иметь цепи сдвига влево, регистр множимого – цепи сдвига вправо.

При этом методе регистр множимого и сумматор частичных произведений должны иметь двойную длину. Однако, как и третий метод, он не требует дополнительных цепей сдвига для выполнения деления.

При четвертом методе, в котором сумма частичных произведений неподвижна, можно совмещать во времени операции сдвига и сложения и за этот счет увеличить быстродействие АЛУ при выполнении умножения (деления).

При любом методе умножения операция обычно начинается с анализа на «0» сомножителей. При равенстве нулю хотя бы одного сомножителя умножение не производится, а произведению присваивается нулевое значение.

Рассмотрим более подробно наиболее распространенный метод умножения чисел, начиная, с младших разрядов со сдвигом суммы частичных произведений вправо.