14

ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПРОГРАММА И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К РЕШЕНИЮ ЗАДАЧ ПО МЕТОДАМ ОПТИМИЗАЦИИ

“Принцип лагранжа в гладких

КОНЕЧНОМЕРНЫХ ЗАДАЧАХ”

Составили: Бигильдеев С.И., Ухоботов В.И.

ЧЕЛЯБИНСК

1983

Многие задачи на отыскание минимального или максимального значения некоторой величины сводятся к задаче о нахождении экстремума функции многих переменных при наличии ограничений типа равенств и неравенств. Необходимым условием экстремума в таких задачах является правило множителей Лагранжа.

Зададим функции , i=0,1,…,m, …,k и некоторое множество . Рассматривается следующая задача:

Определение 1.1. Точка называется точкой абсолютного минимума задач , если она удовлетворяет ограничениям (I.2),(I.3),(I.4) и для любой точки , удовлетворяющей этим же ограничениям, выполняется неравенство .

Замечание. Точки абсолютного минимума задачи будем, следуя [1], обозначать absmin .

Так как не существует сколько-нибудь общих методов нахождения точек абсолютного минимума, то обычно ищут точку локального минимума, а затем проверяют – является ли она точкой absmin или нет.

Определение 1.2. Точка называется точкой локального минимума задач , если она удовлетворяет ограничениям (1.2),(1.3),(1.4) и существует некоторая окрестность точки , что для любой точки из этой окрестности и удовлетворяющей ограничениям (I.2),(I.3),(I.4), выполнено неравенство .

Замечание. Точки локального минимума задачи будем обозначать locmin .

Пример 1. На рис.1 точка – точка абсолютного минимума функции , а точка – точка локального минимума.

(ξ)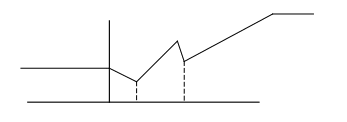

Упражнение. Доказать, что если  absmin , то  locmin .

2.Существование решения.

После того, как реальная задача формализована в виде задачи , естественно возникает вопрос о существовании решения. Этот вопрос обычно решается с помощью теоремы Вейерштрасса (см. [1], стр.23; [2], стр.95).

Теорема Вейерштрасса. Пусть функции (i=0,.....,k) являются непрерывными и существует число , при котором множество

является замкнутым непустым и ограниченным. Тогда существует точка  absmin .

3.Необходимые условия локального минимума.

Установив, с помощью теоремы Вейерштрасса или каким-то другим способом, факт существования точки абсолютного минимума, переходим к следующему этапу решения задачи – отбор всех точек, “подозреваемых” в экстремальности. Это осуществляется с помощью необходимых условий локального минимума, которые называются правилом множителей Лагранжа (см. [1-4]).

^

Теорема (см [4],§4). Пусть 1) точка =( ) я

^

вляется точкой локального минимума задачи

^

^

(ξ)

(ξ)

(ξ)

и внутренней точкой множества ; 2) функции (i=0,1,...,k) имеют непрерывные частные производные в некоторой окрестности точки .

Тогда существуют числа _, не все равные нулю, такие, что выполнены следующие условия:

1)условие стационарности

(3.1)

2)условие согласования знаков

(3.2)

3)условие пополняющей нежесткости

(3.3)

Замечание. Числа носят название множителей Лагранжа.

Составим функцию Лагранжа для задачи .

Тогда условия стационарности можно записать в следующем виде

Замечание. При нахождении точек локального минимума с помощью правила множителей Лагранжа имеем n+k+1 неизвестных , n уравнений (3.1), m уравнений связи (1.2) и k-m уравнений (3.3). Таким образом, число неизвестных больше на единицу, чем число уравнений, которые имеются для их определения. Однако, условия (3.1), (3.2), (3.3) не изменятся, если все множители Лагранжа умножить на одно и то же положительное число, то есть они определяются с точностью до положительного коэффициента пропорциональности. Поэтому особый интерес представляет случай . Тогда можно считать, что . В общем случае нельзя считать, что (см. пример из [2] стр. 48).

4.Достаточные условия и ответ задачи.

После того, как с помощью необходимых условий найдены все “подозреваемые” в экстремальности точки, следует выбрать из них точки абсолютного минимума. Иногда бывает полезным следующий приём: если только одна точка “подозреваемая” на экстремальность, и если известно, что существует точка абсолютного минимума в задаче , то эта “подозреваемая” точка и будет решением задачи .

Пусть найдено решение . После этого нужно осуществить “выход” из формализованной задачи . Это значит, что нужно “перевести” полученное решение на тот язык, на котором была сформулирована исходная задача.

5.Программа решения задач.

Рекомендуется при решении задач на нахождение минимальных значений придерживаться следующей программы (см. [2], стр.94).

1.Формализация задачи.