
- •Вектор скорости
- •Ускорение, направлено в сторону вогнутости траектории.
- •Пример 3. При условии предыдущей задачи определить ускорение в т. А1, а2 и груза 4 через 1,5 с. После начала вращения. Время разгона равно 2 с., движение считаем равноускоренным.
- •2. Плоское или плоскопараллельное движение
- •5. Решая систему двух уравнений, найдем
- •Абсолютное ускорение
Кинематика
Кинематикой называют раздел теоретической механики, в котором изучают механическое движение, рассматриваемое без учета сил, приложенных к движущимся объектам. Другими словами, кинематика исследует изменения положения тел в пространстве, происходящие с течением времени.
Кинематика точки
Способы задания движения: естественный, векторный и координатный.
Движение тела или материальной точки считают известным, если существует возможность определить их положение относительно выбранной системы отсчета в любой момент времени. Задание движения точки может быть осуществлено естественным или
координатным способами. Геометрическое место всех положений движущейся точки М называют её траекторией.
Естественный способ определения движения точки
П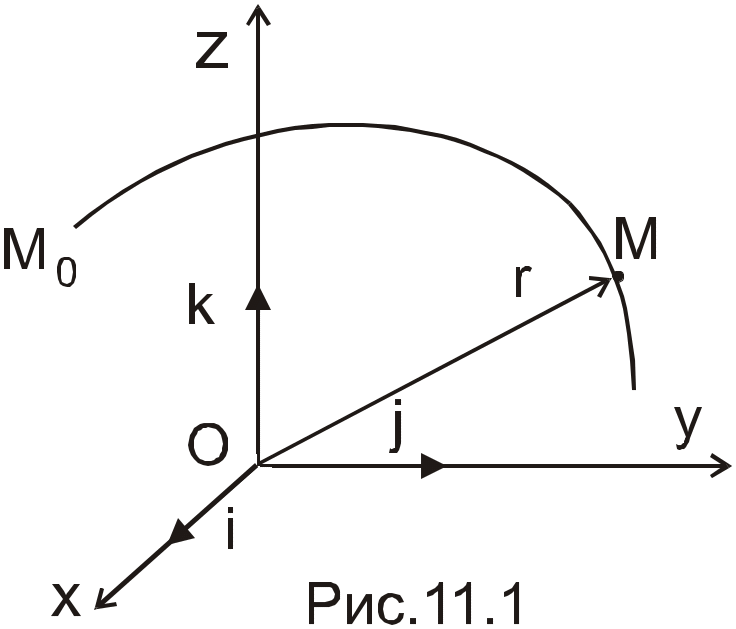 ри
естественном способе определения
движения точки должны быть известны ее
траектория и дуговая координата как
функция времени s=s(t).
Должно быть указано также начало отсчета
и положительное направление движения.
ри
естественном способе определения
движения точки должны быть известны ее
траектория и дуговая координата как
функция времени s=s(t).
Должно быть указано также начало отсчета
и положительное направление движения.
Скорость точки направлена по касательной к траектории, а ее величина и направление определены величиной и знаком производной
![]() .
.
![]()
В екторный
способ задания движения
екторный
способ задания движения
Положение
точки М в пространстве определяется её
радиус–вектором
![]() .
Траекторией является геометрическое
место концов вектора
.
Траекторией является геометрическое
место концов вектора
![]()
Вектор скорости
Скоростью точки М, определяющей как быстро и в каком направлении она движется в данный момент времени t, называют предел
![]()
Вектор скорости равен первой производной от радиуса-вектора точки по времени.
Так
как предельным положением секущей ММ1
является касательная к траектории
точки, то и вектор ее скорости
![]() в данный момент времени t
направлен по касательной к траектории
в сторону движения.
в данный момент времени t
направлен по касательной к траектории
в сторону движения.
Вектор ускорения
В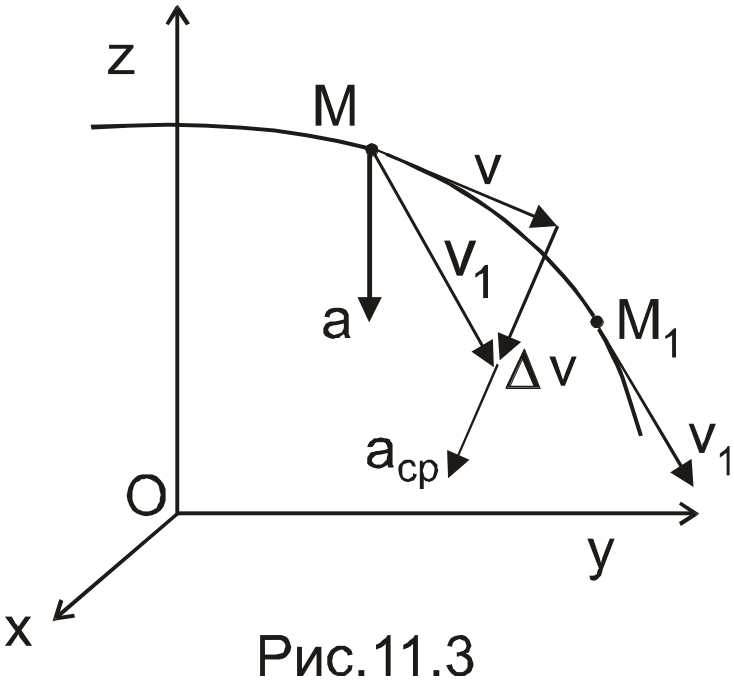 еличину
еличину
![]() называют средним ускорением точки за
время
называют средним ускорением точки за
время
![]() .
Предел отношения
.
Предел отношения
![]() ,
,
характеризующий изменение скорости в данный момент времени t, называют ускорением точки. Вектор ускорения равен первой производной от вектора скорости точки по времени или второй производной от радиуса-вектора точки по времени.
Ускорение, направлено в сторону вогнутости траектории.
Координатный способ задания движения
В
прямолинейной системе координат Oxyz
вектор
![]() может быть представлен в виде
может быть представлен в виде
![]() ,
,
![]() координаты точки
М, определяющие закон ее движения в
зависимости от времени t
;
координаты точки
М, определяющие закон ее движения в
зависимости от времени t
;
![]() -
нормированный базис Oxyz.
-
нормированный базис Oxyz.
1. Проекции скорости на оси координат равны первым производным от соответствующих координат точки по времени:
![]()
2. Проекции ускорения на оси координат равны первым производным от проекций скоростей точки или вторым производным от соответствующих координат точки по времени:

Величины (модули) скорости и ускорения в декартовой ортогональной системе координат определяют по формулам
![]() ,
,
а
направления
![]() и
характеризуют их направляющие косинусы
и
характеризуют их направляющие косинусы
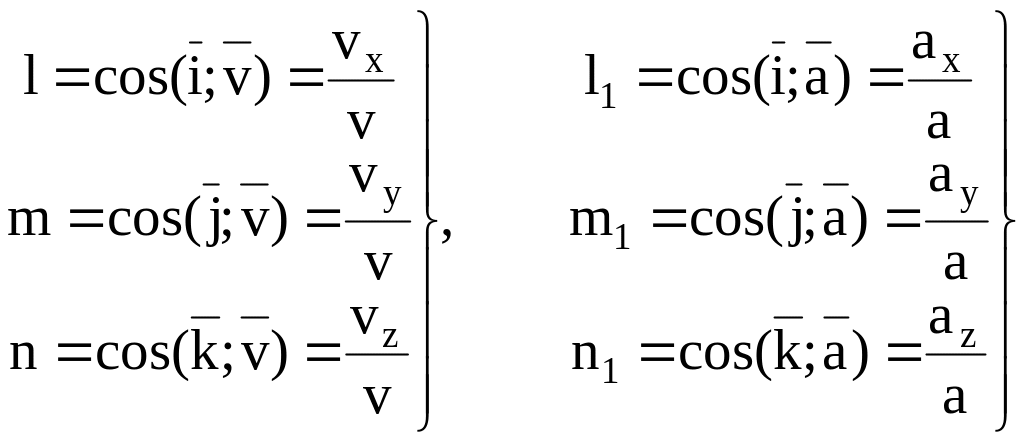 .
.
Задание движения в естественных осях
Предельное
положение прямой, проходящей через
точки М
и М1
траектории L
точки М, когда М1
стремится к М, определяет касательную
к этой кривой в точке М. Обозначим
![]() - единичный направляющий вектор
касательной к L
в точке М.
- единичный направляющий вектор
касательной к L
в точке М.
Соприкасающаяся плоскость в точке М кривой L определяется как предельное положение плоскости, содержащей в себе касательную в точке М кривой и любую точку М1 на ней, когда М1 стремится к М.
Нормаль
![]() к кривой в точке М, лежащую в соприкасающейся
плоскости, называют главной
нормалью к
кривой в т.М. Нормаль
к кривой в точке М, лежащую в соприкасающейся
плоскости, называют главной
нормалью к
кривой в т.М. Нормаль
![]() к кривой, перпендикулярную соприкасающейся
плоскости, называют бинормалью.
к кривой, перпендикулярную соприкасающейся
плоскости, называют бинормалью.
Прямоугольную
систему взаимно ортогональных осей,
направленных по
![]() называют естественными
осями кривой L.
Направление вектора скорости принимают
за положительное направление касательной
.
называют естественными
осями кривой L.
Направление вектора скорости принимают
за положительное направление касательной
.
П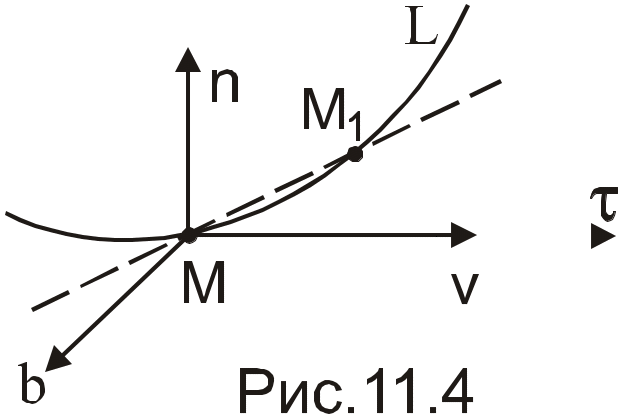

 оложительное
направление главной нормали считают в
сторону вогнутости кривой, а бинормаль
направляют так, чтобы получившаяся
система осей
являлась правой.
оложительное
направление главной нормали считают в
сторону вогнутости кривой, а бинормаль
направляют так, чтобы получившаяся
система осей
являлась правой.
К ривизной
«k»
кривой L
в точке М
называют предел
ривизной
«k»
кривой L
в точке М
называют предел
![]() .
.
Радиусом кривизны «» кривой L в точке М называют величину обратную ее кривизне в этой точке
![]() .
.
Так,
например, дуга окружности длиной s,
опирающаяся на центральный угол
![]() :
:
![]() ,
,
где
R
– радиус окружности, то радиус
кривизны
для окружности
![]()
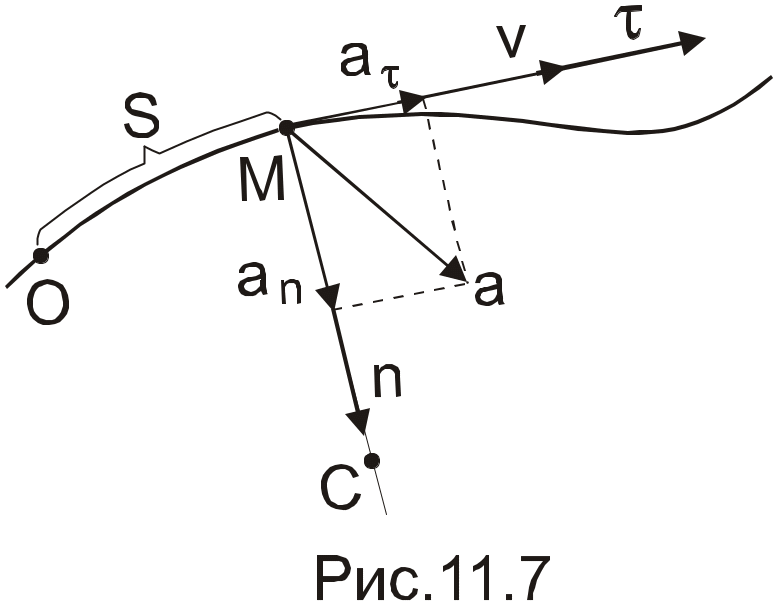
Ускорение
точки можно разложить на тангенциальное
![]() ,
направленное по касательной к траектории
и характеризующее изменение величины
скорости, и нормальное
,
направленное по касательной к траектории
и характеризующее изменение величины
скорости, и нормальное
![]() ,
направленное по главной нормали к центру
кривизны траектории и определяющее
изменение направления
.
,
направленное по главной нормали к центру
кривизны траектории и определяющее
изменение направления
.
 Так
как в естественных осях траектории
скорость может быть представлена в виде
Так
как в естественных осях траектории
скорость может быть представлена в виде
![]() ,
то, дифференцируя это соотношение по
времени, получим ускорение:
,
то, дифференцируя это соотношение по
времени, получим ускорение:
![]() ,
Касательное ускорение
(проекция ускорения точки на касательную)
равно первой производной от величины
скорости от времени:
,
Касательное ускорение
(проекция ускорения точки на касательную)
равно первой производной от величины
скорости от времени:
![]()
Нормальное ускорение
![]()
Абсолютная
величина
![]() может быть определена по формуле
может быть определена по формуле
![]() .
.
Задача. По заданным уравнениям движения точки
x
= 2t
(см),
![]() (см)
(см)
определить ее траекторию, положение, скорость, ускорение, касательное и нормальное ускорения, радиус кривизны траектории в заданное время t1 = 2c.
Решение.
 .Уравнение
траектории получим, исключив из уравнений
движения время:
.Уравнение
траектории получим, исключив из уравнений
движения время:
![]() -
парабола с вершиной в точке (0,-2).
-
парабола с вершиной в точке (0,-2).
Построим
траекторию по точкам:

2.Величина
скорости точки
![]() ;
;
![]() см/с;
см/с;
![]() ;
при t1=2с,
vx=2
см/с vy=6см/с;
;
при t1=2с,
vx=2
см/с vy=6см/с;
![]()
3.
Величина ускорения точки
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
4.Касательное
ускорение
![]() ; при t1
= 2с
; при t1
= 2с
![]() .
.
5.Нормальное
ускорение
![]() ;
;
при
t1
= 2c
:
![]() .
.
6.Радиус
кривизны траектории
![]()
![]() ;
при t1
= 2c
;
при t1
= 2c
![]() см.
см.
Кинематика твердого тела
Твердые тела можно рассматривать как совокупность точек, расстояния между которыми в процессе их перемещения остаются неизменными. Угол между пересекающимися прямыми, связанными с телом, сохраняется без изменения, а параллельные прямые остаются параллельными при его движении. Положение точек твердого тела полностью определено, если известно положение трех его точек, не лежащих на одной прямой.
1. Простейшие движения твердого тела
К простейшим относятся поступательное и вращательное движение тела вокруг неподвижной оси.
1.1. Поступательное движение. При поступательном движении любой отрезок прямой (например, отрезок АВ), проведенный в твердом теле, остается параллельным самому себе.
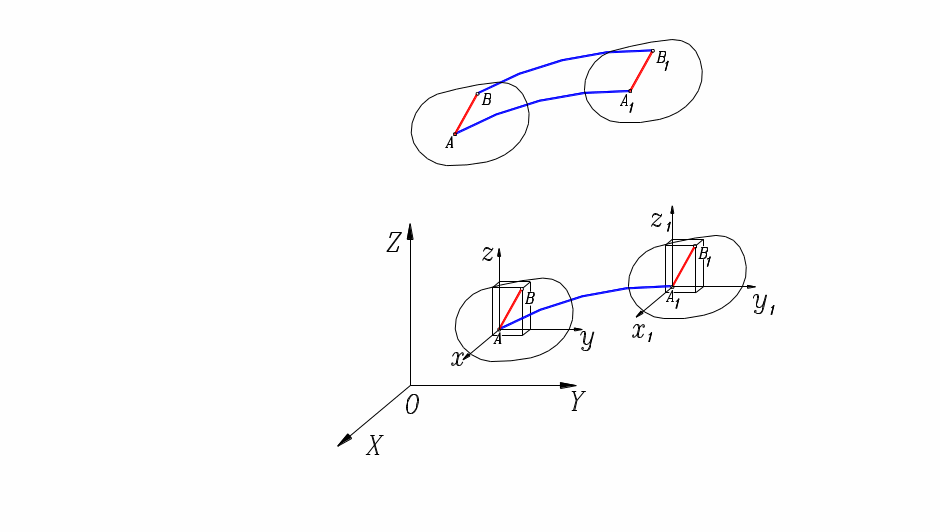
Выберем подвижную систему отсчета Axyz , оси которой связаны с данным телом и передвигаются вместе с ним.
Т. к. при поступательном движении оси координат остаются параллельными своему начальному направлению, координаты любой точки (например т. В) твердого тела в подвижной системе отсчета остаются постоянными, а ее движение тождественно движению т. А.
Следовательно, траектории движения всех точек одинаковы. Одинаковыми по модулю и направлению будут также скорости и ускорения твердого тела при его поступательном движении.
Поступательное движение твердого тела полностью определяется движением одной его точки.
Все точки тела движутся по идентичным траекториям, а их скорости и ускорения одинаковы.
Скорости и ускорения при простейших движениях точек тела при его
поступательном движении
Равномерное прямолинейное движение (v=const) по оси Х
x=x0+vt, a=0.
Равномерное криволинейное движение (v=const)
s=s0+vt,
![]()
где s − дуговая координата; s0 − дуговая координата в начальный момент времени при t=0.
Равноускоренное движение (a=const)
v=v0+
аτ
t
![]()
здесь v0 − начальная скорость при t=0.
1.2. Вращательное движение твердого тела
Вращательным движением называется такое движение, при котором любые две точки, принадлежащие телу, остаются неподвижными.
П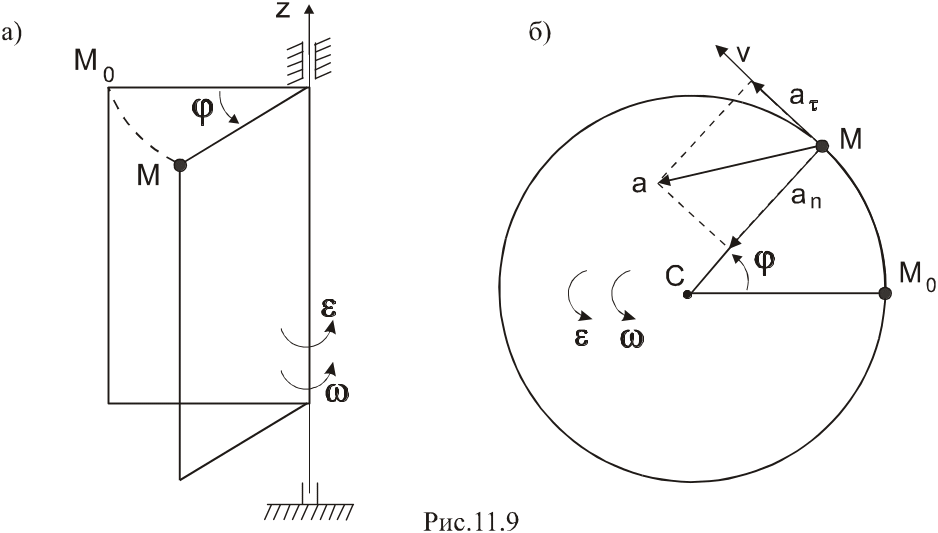 рямая,
соединяющая эти точки называется осью
вращения все точки этой прямой также
остаются неподвижными. Остальные точки
тела движутся по окружностям в параллельных
плоскостях, перпендикулярных оси
вращения, а их центры расположены на
оси вращения.
рямая,
соединяющая эти точки называется осью
вращения все точки этой прямой также
остаются неподвижными. Остальные точки
тела движутся по окружностям в параллельных
плоскостях, перпендикулярных оси
вращения, а их центры расположены на
оси вращения.
Такое движение вполне определяется углом поворота тела относительно некоторого начального положения:
![]()
За
время t
угол
изменяется на величину .
Отношение
к t
называют средней угловой скоростью
тела за время t
,
![]() .
.
Угловая скорость тела:
![]() .
.
Угловая скорость тела равна первой производной от угла поворота по времени.
Отношение
к t
называют средним угловым ускорением
![]() .
Угловое ускорение:
.
Угловое ускорение:
![]()
Угловое ускорение тела равно первой производной от угловой скорости по времени.
Перемещения
S
и скорости точек
![]() можно
определить из соотношений:
можно
определить из соотношений:
S
=![]() ;
;
здесь R − радиус вращения.
![]() .
.

Нормальное
(центростремительное)
![]() и
тангенциальное (вращательное)
и
тангенциальное (вращательное)
![]() ускорения
определим из соотношений:
ускорения
определим из соотношений:
![]() ,
,
![]() ;
;
![]() ,
,
![]()
Полное ускорение точки:
![]() .
.
Модули скоростей и ускорений точек вращающегося тела пропорциональны расстояниям от этих точек до оси вращения.
Равнопеременное вращение тела
При равнопеременном вращении твердого тела вокруг неподвижной оси: ε= const
Так
как
![]()
После интегрирования с учетом начальных условий получим:
ω=ω0+ε t
φ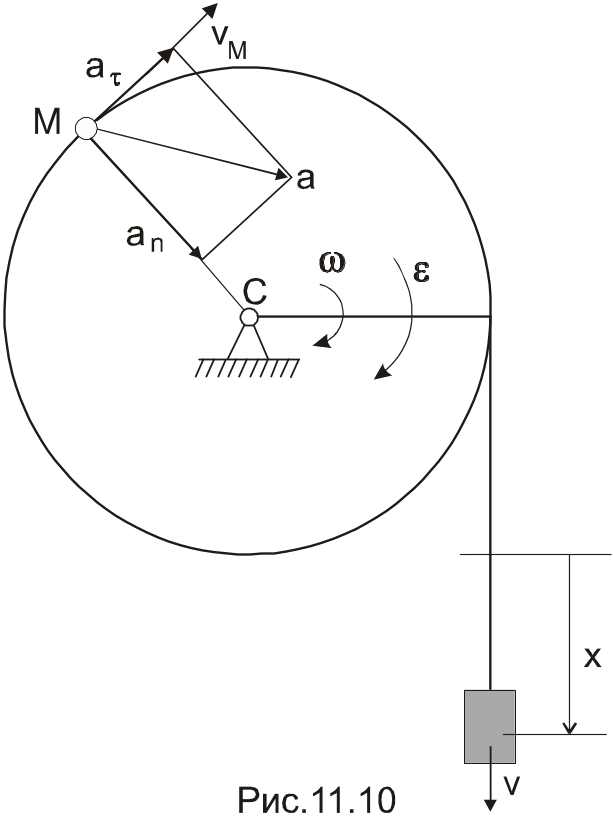 =φ0
+ω0t+ε
t2/2,
здесь ω0
и φ0
− угловая скорость и угол поворота в
начальный момент времени при t=0.
=φ0
+ω0t+ε
t2/2,
здесь ω0
и φ0
− угловая скорость и угол поворота в
начальный момент времени при t=0.
Пример
1.
Груз, опускаясь согласно уравнению
![]() (м), приводит посредством троса в движение
барабан радиуса R
= 0,2м (рис.11.10). Определить скорость и
ускорение точки М барабана при t1=
2с.
(м), приводит посредством троса в движение
барабан радиуса R
= 0,2м (рис.11.10). Определить скорость и
ускорение точки М барабана при t1=
2с.
Решение. Скорость груза равна скорости точки М барабана
![]() Угловая
скорость барабана:
Угловая
скорость барабана:
![]() .
.
Угловое
ускорение
![]() .
.
При
t1=2c:
![]() ,
,
![]() ;
;
![]()
Нормальное ускорение:
![]() ,
,
Тангенциальное ускорение:
![]() ,
,
Полное ускорение:
![]() .
.
Пример 2. Вал 1 с зубчатым колесом 1 при вращении делает n=300 об./мин. Колесо 1 находится в зацеплении с зубчатым колесом 2. Радиусы делительных окружностей колес составляют R1=10 см, R2=50 см. На валу 2 смонтирован барабан 3 радиуса R3= 20 см, который вращается вместе с зубчатым колесом 2. Найти скорость перемещения груза 4, подвешенного на тросе.

Решение. 1. Угловая скорость колеса 1:
ω1= n/ 30 = 10 с−1
2. Линейные скорости точек, колес 1, 2 в точках контакта А равны в любой момент времени:
vA=ω1R1=ω2R2 = 100 см/с
такую же скорость имеют точки А1, А2 .
3. Угловая скорость колеса 2 и барабана 3:
ω2= ω1R1 /R2= 2 с−1
4. Скорость перемещения груза 4, такую же скорость имеют точки на наружной поверхности барабана (например, т. А3):
v4=ω2R3= 40 см/с
