
- •Глава 4.
- •Глава 6.
- •Глава 9.
- •Глава 10.
- •Глава 11.
- •Глава 12.
- •Глава 13.
- •Глава 14.
- •Глава 15.
- •Глава 16
- •Глава 18
- •Глава 1.
- •§ 1. Аксиомы и принципы статики твёрдого тела.
- •§ 2. Момент силы относительно произвольного центра, оси.
- •§ 3. Пара сил и её свойства.
- •§ 4.Главный вектор и главный момент системы сил. Правило Пуансо.
- •§ 5. Приведение системы сил к простейшему виду.
- •§ 6. Уравнения равновесия тела.
- •Глава 2. Центр параллельных сил и центр тяжести.
- •§ 1. Центр параллельных сил.
- •§ 2. Центр тяжести, методы определения координат центра тяжести.
- •Глава 3. Равновесие при наличии сил трения.
- •§ 1. Трение скольжения Угол трения, конус трения.
- •§ 2. Задача об опрокидывании тела. Трение качения.
- •Кинематика
- •Глава 4. Кинематика точки.
- •§ 1. Способы задания движения точки. Уравнения движения точки; траектория.
- •§ 2. Натуральный триэдр траектории.
- •§ 3. Скорость точки.
- •§ 4. Ускорение точки.
- •§ 5. Поступательное движение твердого тела.
- •Глава 5. Вращение твердого тела вокруг неподвижной оси.
- •§ 1 Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси.
- •§ 2. Векторные формулы скорости и ускорения точек тела, вращающегося вокруг неподвижной оси.
- •Глава 6. Кинематика плоского движения твердого тела
- •§ 1. Уравнения плоского движения.
- •§ 2. Скорости точек плоской фигуры.
- •§ 3. Мгновенный центр скоростей плоской фигуры.
- •§ 4. Ускорения точек плоской фигуры.
- •Глава 4. Вращение тела вокруг неподвижной точки. Общий случай движения тела.
- •§ 1. Определение положения твердого тела, имеющего неподвижную точку.
- •§ 2 Углы Эйлера, матрицы поворота.
- •§ 3. Угловая скорость и угловое ускорение твердого тела, имеющего неподвижную точку.
- •§ 4. Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижного центра.
- •Глава 6.
- •§ 5. Определение положения твердого тела в пространстве.
- •§ 6. Скорости и ускорения в общем случае движения твердого тела.
- •Глава 8. .Кинематика относительного движения точки и тела.
- •§ 1. Абсолютное, относительное и переносное движения.
- •§ 2. Теорема о сложении скоростей в относительном движении.
- •§ 3. Сложение ускорений, теорема Кориолиса.
- •§ 4. Сложение вращений твёрдого тела.
- •§ 5. Общий случай движения тела (для скоростей).
- •Динамика точки и твёрдого тела
- •Глава 9. Динамика точки.
- •§ 1. Основные положения и аксиомы динамики
- •§ 2. Дифференциальные уравнения движения материальной точки.
- •§ 3. Динамики относительного движения точки.
- •Глава 10. Количество движения системы.
- •§ 1. Уравнения динамики системы материальных точек и твёрдого тела.
- •§ 2. Теорема об изменении количества движения системы материальных точек.
- •§ 3. Теорема о движении центра масс.
- •Глава 11. Кинетический момент системы и твёрдого тела.
- •§ 1. Теорема об изменении главного момента количества движения системы материальных точек.
- •§ 3. Кинетический момент тела, вращающегося относительно неподвижной точки.
- •§ 3. Момент инерции относительно произвольной оси. Тензор инерции.
- •§ 4. Главные оси инерции и главные моменты инерции.
- •§ 5. Вычисление моментов инерции.
- •§ 6. Преобразование моментов инерции.
- •§ 7. Кинетический момент твердого тела.
- •Глава 12. Дифференциальные уравнения движения твердого тела.
- •§ 1. Дифференциальные уравнения вращения твердого тела.
- •§ 2. Общий случай движения твердого тела.
- •§ 3. Динамика плоско-параллельного движения тела.
- •§ 4. Реакция оси вращающегося тела.
- •§ 5. Задача о физическом маятнике.
- •Глава 13. Кинетическая энергия системы и твёрдого тела.
- •§ 1. Кинетическая энергия системы материальных точек.
- •§ 2. Кинетическая энергия твердого тела.
- •§ 3. Работа силы. Мощность.
- •§ 4. Примеры вычисления потенциальной энергии и работы
- •§ 5. Теорема об изменении кинетической энергии.
- •§ 6. Закон сохранения механической энергии.
- •Динамика несвободной системы. __________________________________________________________Глава 14. Возможные перемещения.
- •§1. Связи, классификация связей, число степеней свободы.
- •§2. Возможные перемещения.
- •§ 3. Принцип освобождаемости. Идеальные связи.
- •§ 4. Статический принцип возможных перемещений.
- •§ 5. Динамический принцип возможных перемещений. Общее уравнение динамики.
- •Глава 15. Уравнение Лагранжа второго рода и его приложения.
- •§ 1. Вывод уравнения Лагранжа второго рода.
- •§ 2. Диссипативная функция.
- •§ 8. Представление кинетической энергии как функции обобщённых скоростей.
- •§ 9. Интеграл энергии.
- •Малые колебания системы с одной степенью свободы.
- •Глава 16 Свободные колебания системы с одной степенью свободы.
- •§ 1. Устойчивость равновесия голономной системы в консервативном силовом поле.
- •§ 2. Малые свободные колебания системы с одной степенью свободы.
- •§ 3. Свободные колебания системы с учётом линейно-вязкого сопротивления.
- •Глава 17.
- •§ 1. Вынужденные колебания без сопротивления. Биения, резонанс.
- •§ 2. Вынужденные колебания системы с учётом линейно-вязкого трения.
- •§ 3. Динамические характеристики вынужденных колебаний.
- •Некоторые задачи статики и динамики точки и твёрдого тела.
- •Некоторые задачи статики и динамики точки и твёрдого тела.
- •Глава 18 Уравнения статики деформируемого твёрдого тела.
- •§ 1. Дифференциальные уравнения равновесия нерастяжимой нити.
- •§ 2. Статика деформируемых прямых стержней.
- •Глава 19. Элементарная теория удара
- •§ 1. Теорема импульсов и её приложения в теории удара.
- •§ 2. Задача Герца о прямом и центральном ударе двух тел.
- •§ 3. Теоремы об изменении количества движения и кинетического момента при ударе.
- •§ 4. Удар, действующий на тело, вращающегося вокруг неподвижной оси.
- •§ 5. Условия отсутствия ударных реакций. Центр удара.
- •1.Статика.
- •2. Кинематика.
- •3. Динамика точки и твердого тела:
- •4. Динамика несвободной системы.
- •5. Колебания системы около положения устойчивого равновесия.
- •Дополнительные вопросы, включаемые по согласованию с выпускающими кафедрами: Динамические характеристики вынужденных колебаний. Нелинейные колебания точки. Метод Ван дер Поля.
- •3. Теорема о движении центра масс.
- •6. Теорема об изменении кинетической энергии.
§ 5. Динамический принцип возможных перемещений. Общее уравнение динамики.
Свободная точка описывается дифференциальным уравнением
![]() ,
(4.15)
,
(4.15)
где - равнодействующая задаваемых сил, приложенных к точке . Рассмотрим несвободную систему с идеальными голономными связями. Обозначая, как и раньше, массы точек через , равнодействующую задаваемых сил через , ускорение точки - , реакции связей через , возможные перемещения через . Тогда уравнения движения точки запишется в виде
![]() .
(4.16)
.
(4.16)
Вычитая (4.16) из (4.15), получим
![]()
Умножим каждое из полученных уравнений на возможное перемещение и просуммируем по всем точкам системы
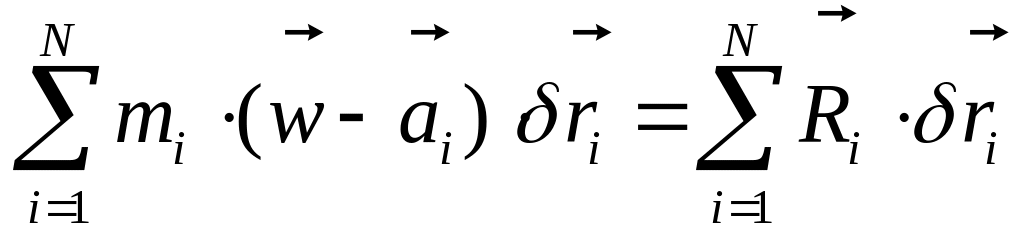 .
(4.17)
.
(4.17)
В случае идеальных связей правая часть уравнения (3.17) равна нулю, тогда с учётом (3.15) имеем
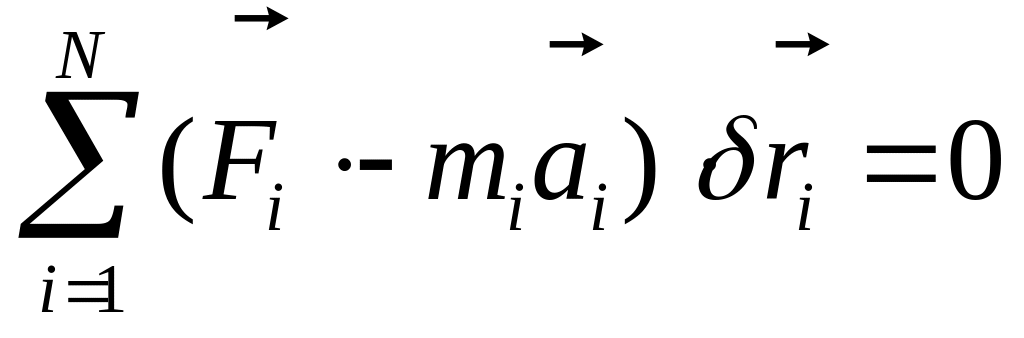 .
(4.18)
.
(4.18)
Это основное, как мы дальше увидим, для всей динамики несвободной системы полученное уравнение получило название общего уравнения динамики.
Глава 15. Уравнение Лагранжа второго рода и его приложения.
§ 1. Вывод уравнения Лагранжа второго рода.
Уравнения
Лагранжа второго рода представляют
дифференциальные уравнения несвободной
системы, составленные в обобщенных
координатах. Наибольшее распространение
получили уравнения в неависимых
обобщенных координатах, — их обычно и
называют уравнениями Лагранжа второго
рода, а иногда просто уравнениями
Лагранжа, так как уравнениями Лагранжа
первого рода пользуются сравнительно
редко. Рассмотрим систему с n
степенями
свободы, подчиненную идеальным голономным
связям. Положение системы в пространстве
будем определять n
независимыми обобщенными координатами
![]() .
Вектор-радиус
любой точки системы может быть выражен
через обобщенные координаты и время,
если связи нестационарны, по формулам
,
а возможные перемещения определятся
как вариации вектор-радиусов;
.
Вектор-радиус
любой точки системы может быть выражен
через обобщенные координаты и время,
если связи нестационарны, по формулам
,
а возможные перемещения определятся
как вариации вектор-радиусов;
.
Так как все обобщённые координаты считаем независимыми, то все представляют произвольные бесконечно малые величины. Докажем предварительно два тождества Лагранжа. Составим выражения векторов скоростей точек системы:
 (4.19)
(4.19)
Производные
обобщенных координат по времени, т. е.
величины
![]() называются обобщенными скоростями.
Формулы (4.19) показывают, что скорость
любой точки линейно выражается через
обобщенные скорости, Поэтому, обозначая
через к
произвольный индекс, изменяющийся от
1 до n,
будем иметь:
называются обобщенными скоростями.
Формулы (4.19) показывают, что скорость
любой точки линейно выражается через
обобщенные скорости, Поэтому, обозначая
через к
произвольный индекс, изменяющийся от
1 до n,
будем иметь:
 (4.20)
(4.20)
Это первое тождество Лагранжа. Докажем второе тождество
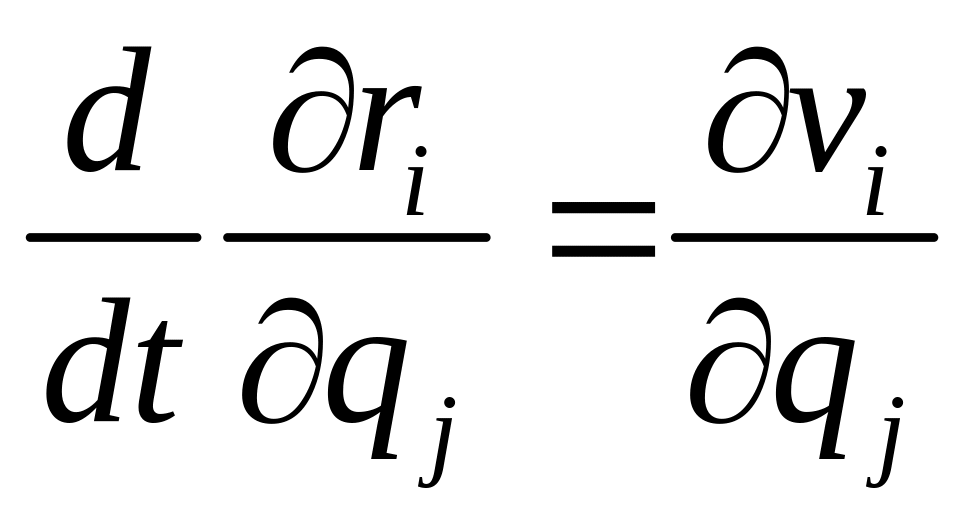 (4.21)
(4.21)
Для
этого, дифференцируя обе части (4.19) по
![]() ,
получим
,
получим
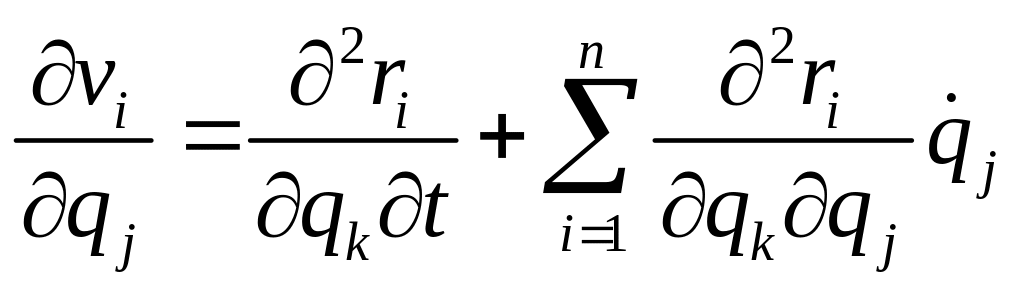
С другой стороны, составим непосредственно
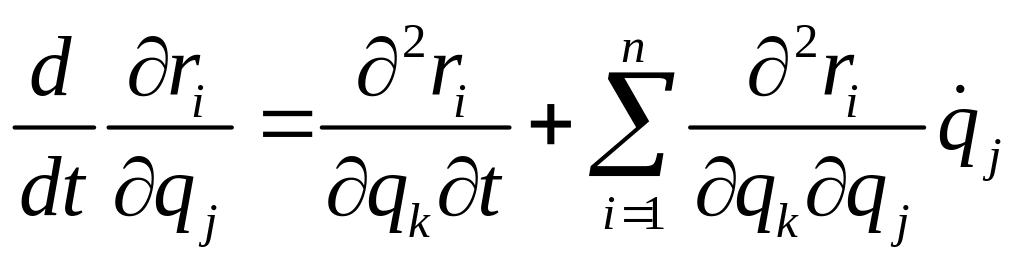
Сравнивая последние два равенства, убеждаемся в справедливости соотношения (4.21). Обратимся к общему уравнению динамики (4.18) и перепишем его в виде
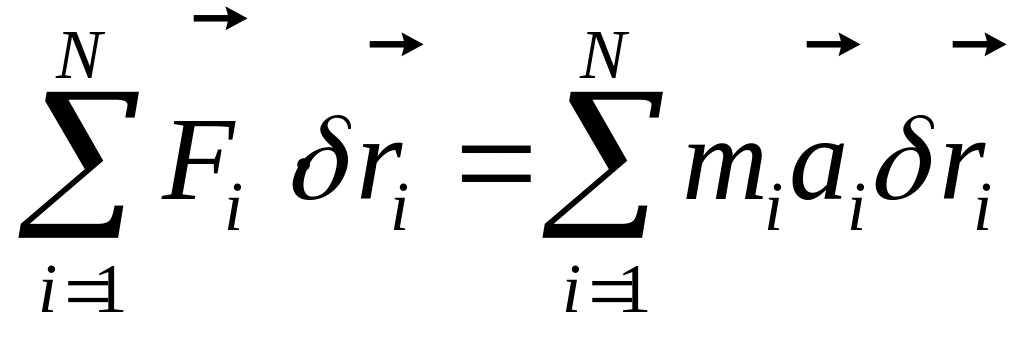 (4.22)
(4.22)
Первая
сумма уже была выражена через обобщенные
координаты (4.11); она равна
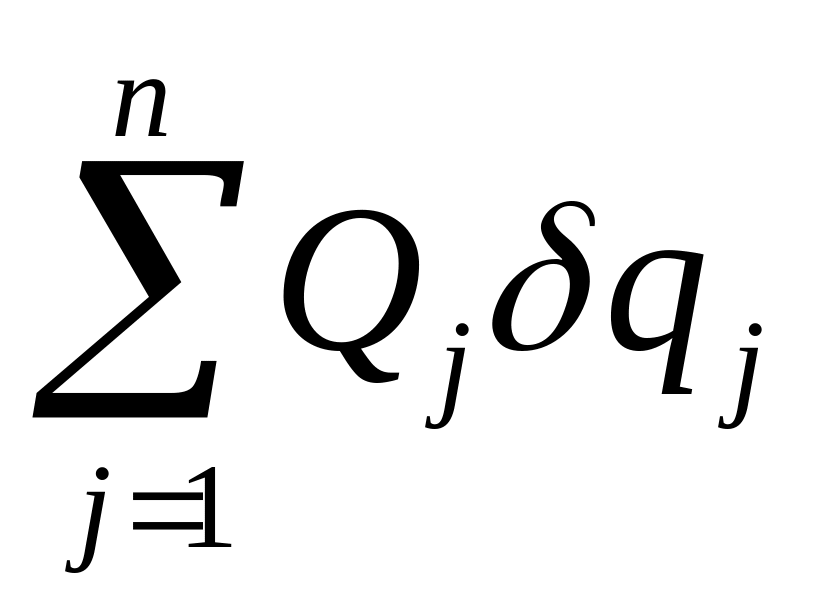 ,
где Qj
— обобщенная сила. Что касается второй
суммы в уравнении (4.22), то ее можно
преобразовать, пользуясь (4.9) и меняя
порядок суммирования:
,
где Qj
— обобщенная сила. Что касается второй
суммы в уравнении (4.22), то ее можно
преобразовать, пользуясь (4.9) и меняя
порядок суммирования:
 (3.23)
(3.23)
скалярное произведение под знаком суммы преобразуется к виду
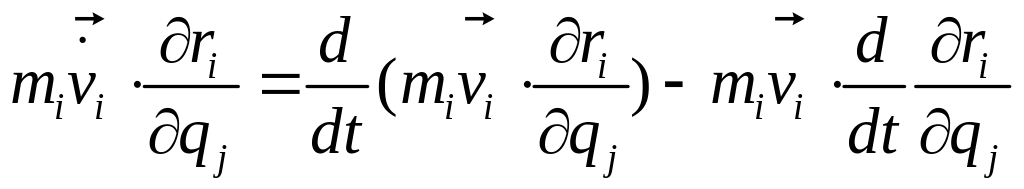 (4.23)
(4.23)
или по формулам (4.20) и (4.21)):

Подставляя
последнее выражение в круглую скобку
правой части равенства (4.23) и замечая,
что сумма
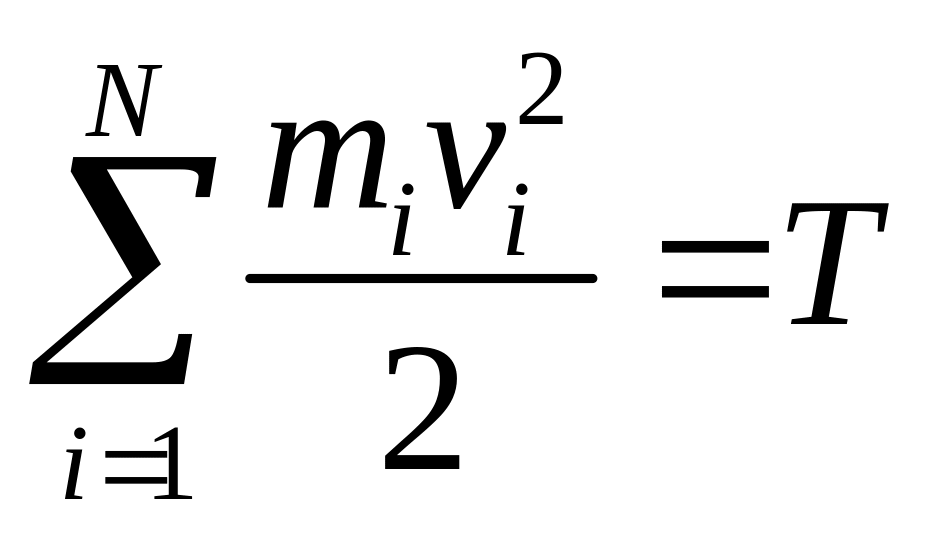 определяет кинетическую энергию системы,
получим:
определяет кинетическую энергию системы,
получим:

Уравнение (4.18) теперь перепишется так:
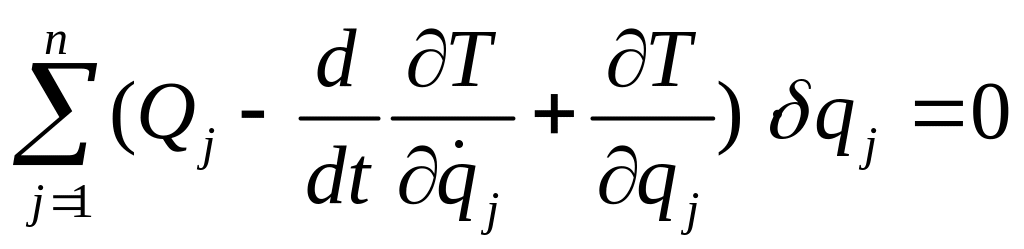 (4.24)
(4.24)
Последнее равенство может выполняться при произвольных , только если все круглые скобки равны нулю. Таким образом, мы приходим к уравнениям Лагранжа второго рода, составленным в независимых обобщенных координатах для системы с голономными связями:
 (4.25)
(4.25)
Уравнения (4.25) представляют совокупность n (по числу степеней свободы) обыкновенных дифференциальных уравнений второго порядка с n независимыми обобщенными координатами, являющимися искомыми функциями времени. Оператор
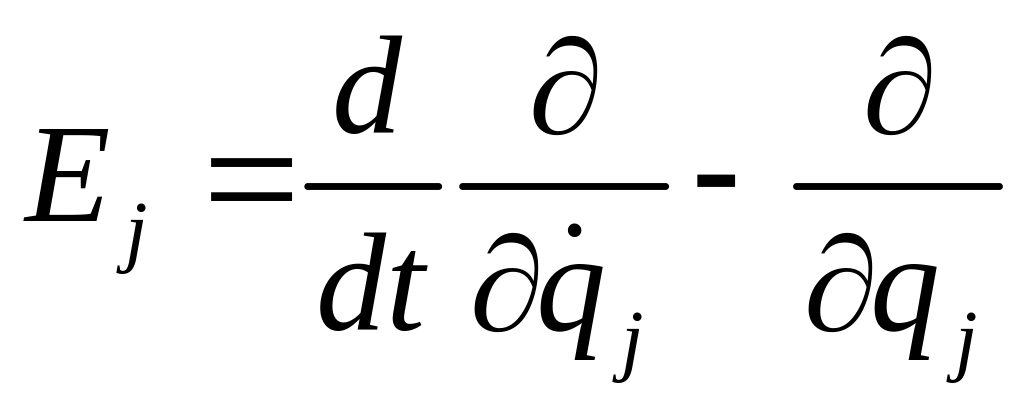 (4.26)
(4.26)
носит
название оператор Эйлера-Лагранжа.
Уравнению Лагранжа второго рода можно
дать и другое доказательство. Как
указывалось выше, положение любой точки
можно представить в виде
![]() ,
где n
- число независимых обобщённых координат,
равное, в нашем случае, числу степеней
свободы системы. Тогда
,
где n
- число независимых обобщённых координат,
равное, в нашем случае, числу степеней
свободы системы. Тогда
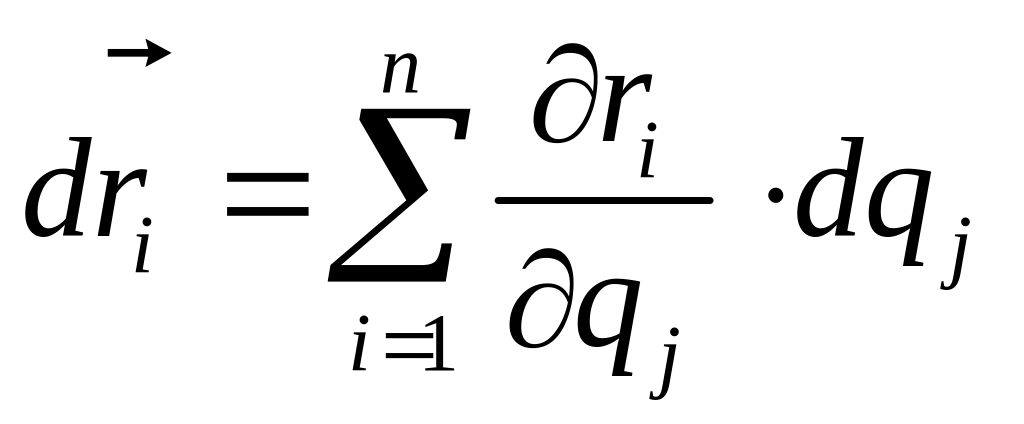 и величину
и величину
![]() можно
представить как направление вдоль
координатной линии
.
Спроектируем основное уравнение динамики
точки на это направление
можно
представить как направление вдоль
координатной линии
.
Спроектируем основное уравнение динамики
точки на это направление
![]()
(при этом есть сумма всех сил: внешних и внутренних, действующих на точку) и сложим все полученные проекции.
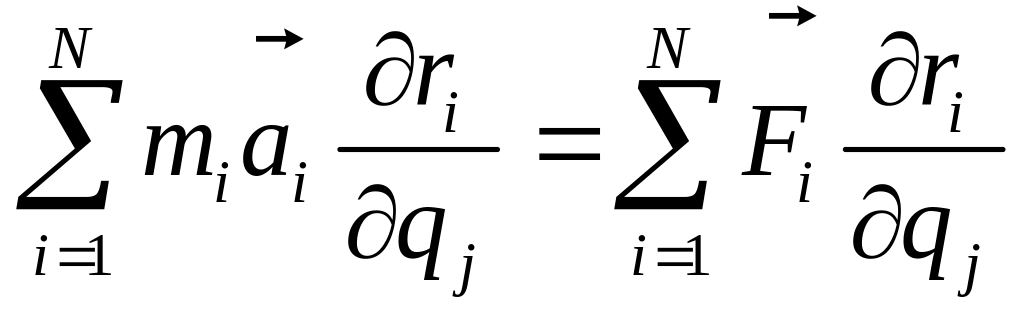 (4.27)
(4.27)
Справа в выражении (4.27) стоит по (4.11) обобщённая сила, а слева выражение (4.23). Проведя аналогичные преобразования, получаем уравнение Лагранжа второго рода.
.
Пример.
Рассмотрим задачу о колебаниях стержня
массы m
и длины l,
подвешенного в точке D
к вращающемуся вокруг вертикальной оси
АВ
стержню АВD.
Момент инерции стержня АВD
равен J.
За обобщённые координаты выберем углы
![]() и φ.
Кинетическая энергия системы в общем
виде запишется в форме
и φ.
Кинетическая энергия системы в общем
виде запишется в форме
![]()
 ,
,
Здесь
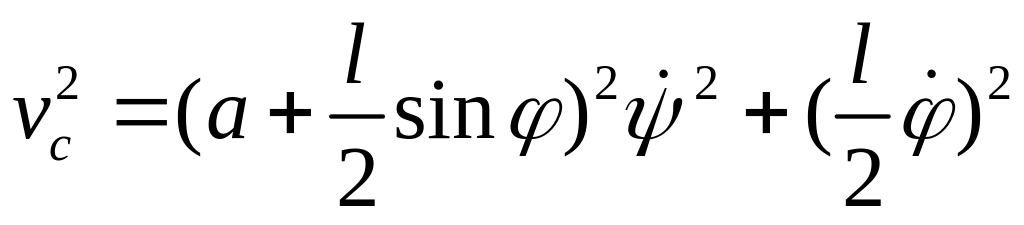 - скорость центра стержня,
- скорость центра стержня,
![]() - вектор угловой скорости стержня,
- вектор угловой скорости стержня,
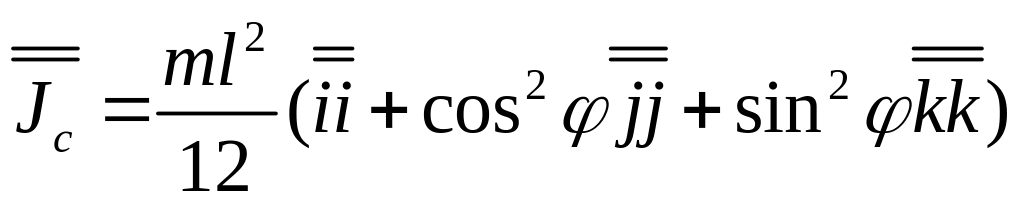 -тензор инерции стержня относительно
центра С.
Подставив введённые обозначения в
формулу для кинетической энергии,
получим
-тензор инерции стержня относительно
центра С.
Подставив введённые обозначения в
формулу для кинетической энергии,
получим
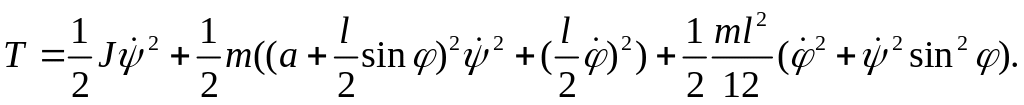
Проведя несложные преобразования, запишем кинетическую энергию в виде
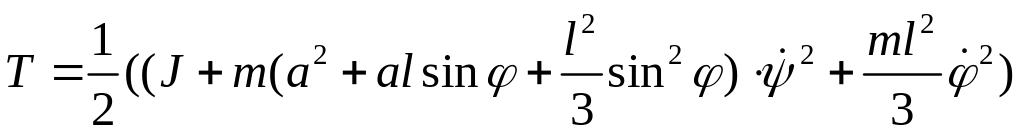
Совсем
нетрудно получить и выражение для
возможной работы сил:момента
![]() и силы тяжести
и силы тяжести
![]() .
.
 .
.
Обобщённые
силы будут
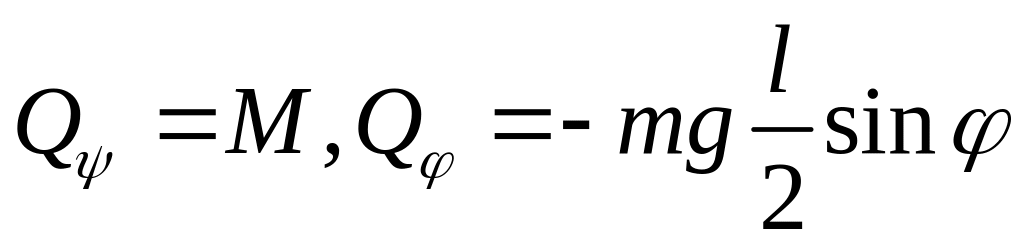 .
Составим уравнения движения с помощью
уравнения Лагранжа второго рода:
.
Составим уравнения движения с помощью
уравнения Лагранжа второго рода:
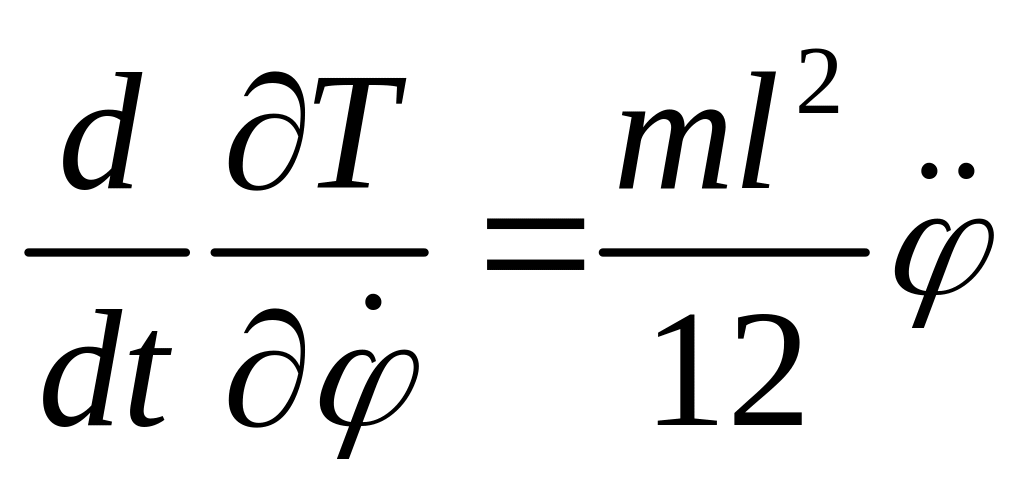 ;
обозначим
;
обозначим
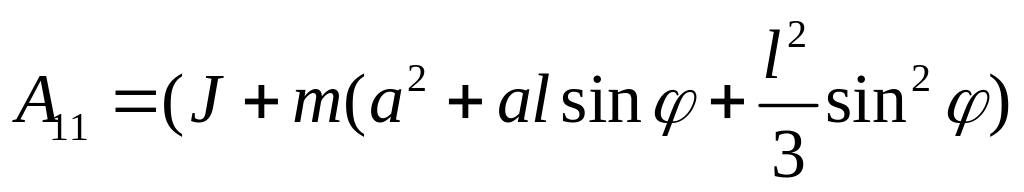 ,
и
,
и
 ,
тогда
,
тогда
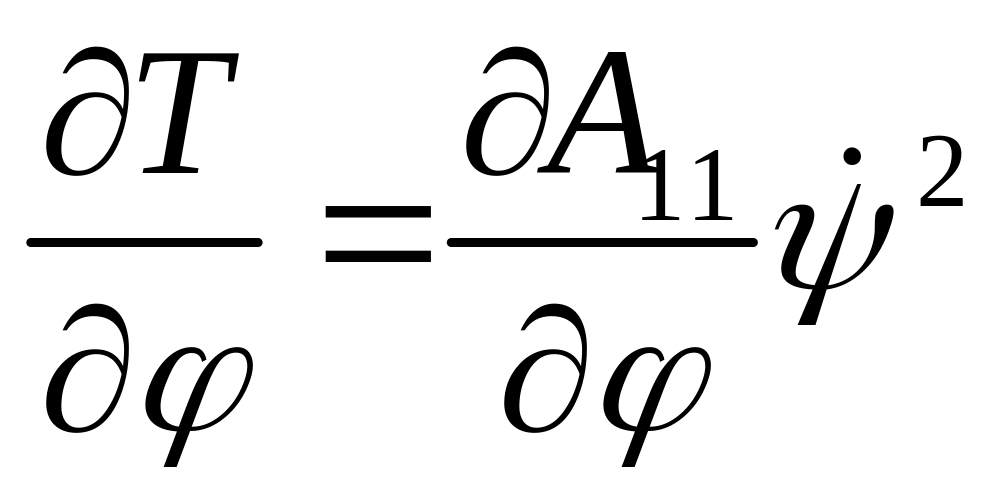 и первое уравнение имеет вид
и первое уравнение имеет вид
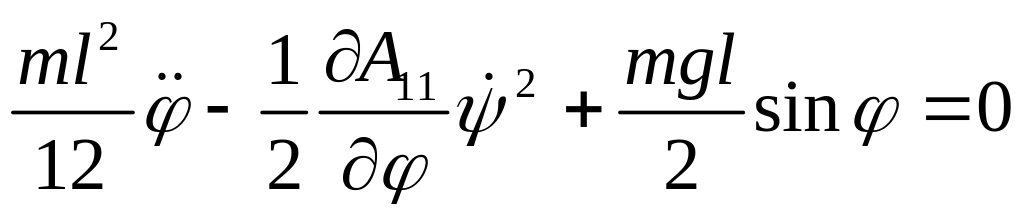 .
.
Второе уравнение будет
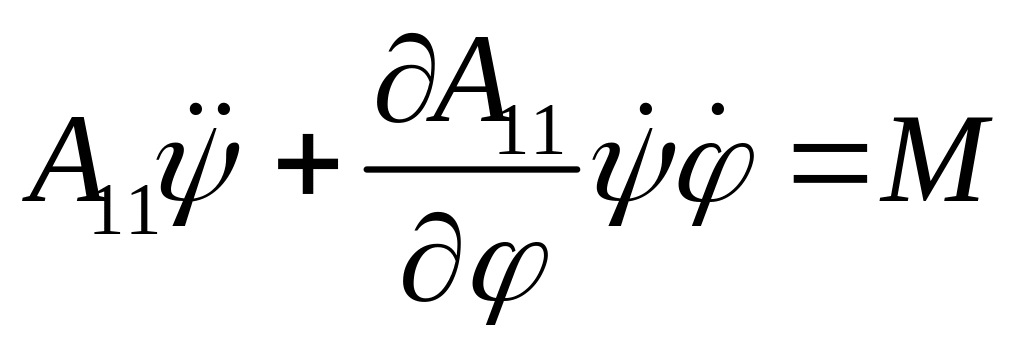 .
.
