Обыкновенными дифференциальными уравнениями (ОДУ) можно описать явления и процессы в самых различных областях естествознания: это и движение системы материальных точек, и прохождение тока через электрические цепи, и развитие популяций животных и др. Вначале мы остановимся на методах решения задачи Коши для ОДУ первого порядка.

1 Методы решения для уравнения первого порядка

Задачей Коши (или начальной задачей) для одного ОДУ первого порядка называется задача решения следующей системы равенств:

(1.1)

Здесь - заданная функция двух переменных. Второе из равенств (1.1) называется начальным условием.

1.1. Метод Эйлера. Пусть решение задачи (1.1) – функцию - требуется получить на отрезке (точка совпадает с левой границей отрезка – точкой ). Разобьём отрезок на маленьких отрезков шириной узлами . Предположим, что решение задачи Коши известно в узле заданного отрезка. Аппроксимируем производную в этом узле при помощи одной из формул численного дифференцирования: ; подставим это выражение в левую часть уравнения (1.1). Преобразуя, получим:

(1.2)

Здесь и далее через обозначаем значение функции в точке . Тогда (1.2) можно переписать в виде

(1.3)

Это и есть формула метода Эйлера. Формула (1.3) показывает, что значение неизвестной функции в точке отрезка интегрирования можно подсчитать по известному значению функции в предыдущей точке . Выясним геометрический смысл формулы (1.2). Как следует из ОДУ (1.1), геометрический смысл его правой части – это тангенс угла наклона касательной к кривой . Тогда вычисление по формуле (1.2) означает, что на плоскости мы проводим отрезок прямой из точки с координатами к точке с координатами . Двигаясь таким образом от узла к узлу на отрезке , мы построим ломаную линию, которая приближает гладкую кривую – решение . Понятно, что чем меньше расстояние между узлами, тем точнее эта ломаная приближает решение. В пределе при стремлении ломаная должна сливаться с кривой – точным решением задачи (1.1). Для того чтобы выяснить, насколько точным является это приближение, сравнивают формулу (1.3) с разложением в ряд Тейлора решения задачи (1.1) в окрестности точки . Нетрудно получить, что

(1.4)

т.е. формула метода Эйлера (1.2) совпадает с разложением в ряд Тейлора (1.4) вплоть до слагаемых, пропорциональных в первой степени при . В этом смысле говорят, что метод Эйлера является методом первого порядка точности.

Пример 1. Дана задача Коши: , . Найти её решение в точке при помощи метода Эйлера. Сравнить теоретическую и реальную погрешность, если точное решение есть функция

(1.5)

Решение. Применим формулу (1.3) при . Получим: = . Для сравнения полученного решения с точным решением разложим функцию (1.5) при в ряд Тейлора в окрестности точки . Получим: . Как видно, точное решение отличается от приближённого на величину порядка при - в полном соответствии с предсказаниями теории.

1.2. Модифицированный метод Эйлера. Попробуем уменьшить погрешность формулы метода Эйлера. Для этого в выражении (1.2) вместо функции возьмём функцию , где , . Если снова привлекать геометрическую интерпретацию, то можно сказать, что теперь отрезок прямой из точки мы проводим в точку с координатами под углом, под которым касательная к кривой проходит в точке . Итак, запишем формулу модифицированного метода Эйлера:

Подставляя сюда вместо их значения, получим:

(1.6)

Для того чтобы оценить порядок погрешности формулы (1.6), разложим стоящую в ней функцию (как функцию двух переменных) в ряд Тейлора в окрестности точки . Продолжая формулу (1.6), получим:

(1.7)

Здесь нижние индексы обозначают частные производные по соответствующим переменным. Сравнивая формулу (1.7) с решением задачи Коши методом Тейлора, можно заметить, что они совпадают вплоть до слагаемых порядка при . В этом смысле говорят, что модифицированный метод Эйлера является методом второго порядка точности. Итак, модификация (1.6) метода Эйлера позволяет строить решение задачи Коши с точностью, которая на порядок выше точности обычного метода Эйлера.

Пример 2. Дана задача Коши: , . Найти её решение в точке при помощи модифицированного метода Эйлера. Сравнить теоретическую погрешность с реальной, если точное решение есть функция, которая задаётся формулой (1.5).

Решение. Применим формулу (1.6) при . Получим: =

. Для сравнения полученного решения с точным решением разложим функцию (1.5) при в ряд Тейлора в окрестности точки . Получим: . Как видно, точное решение отличается от приближённого на величину порядка при - в полном соответствии с предсказаниями теории.

1.3. Методы Рунге-Кутта. Метод Эйлера, модифицированный метод Эйлера и обширное множество других методов решения задачи Коши для ОДУ первого порядка относятся с семейству методов Рунге-Кутта, которые обладают общими для этого семейства родовыми признаками. Перечислим их:

• во-первых, все они одношаговые; это означает, что для вычисления неизвестной функции на шаге (в узле) с номером применяется значение функции только с предыдущего шага ;

• во-вторых, в расчётные формулы не входят производные, а только значения самих функций;

• в-третьих, все эти методы в качестве эталонного используют метод Тейлора, сравнение с которым позволяет определить порядок погрешности данного метода.

Приведём один из часто употребляемых вариантов метода – формулы Рунге-Кутта четвёртого порядка [1]:

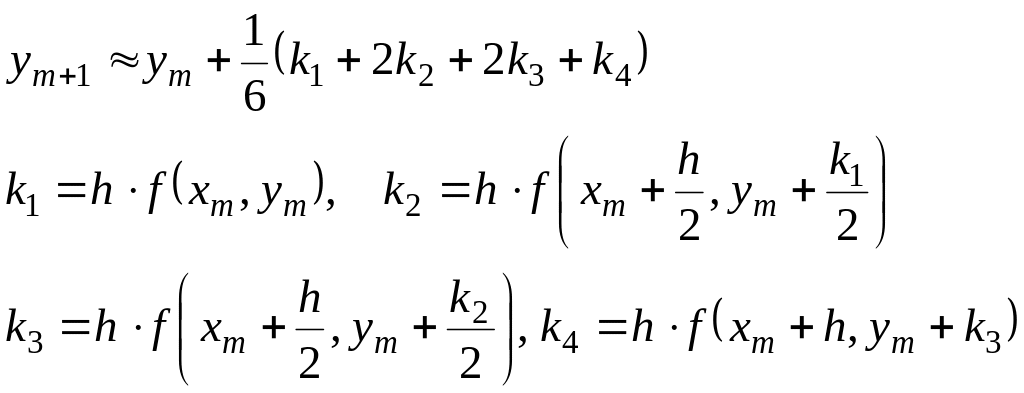(1.8)

1.4. Об устойчивости алгоритма. Наряду с точностью алгоритма одной из важных характеристик является его устойчивость. Например, при одних начальных данных численные результаты могут хорошо соотноситься с точными, а при других – существенно отличаться: в таком случае говорят, что данный алгоритм является неустойчивым по начальным данным. Бывает так, что при исследовании задачи Коши на «небольшом» отрезке времени, наблюдается хорошее согласование между точным и приближённым решениями, а на «большом» отрезке времени происходит их расхождение. Проиллюстрируем сказанное примером [1]. Рассмотрим ОДУ (1.9)

Оно имеет общее решение

(1.10)

Здесь - произвольная постоянная, конкретный вид которой зависит от начального условия. При начальном условии

(1.11)

Точное решение имеет вид

.

Предположим, что начальное условие задано с точностью 1%, т.е. вместо (1.11), на самом деле, должно быть

(1.12)

Нетрудно получить, что в этом случае решение может находиться в пределах от

до

.

Тогда при ошибка в определении может достигать , т.е. около 30%, в то время как в начальном условии (1.12) она составляла всего 1%. Таким образом, ошибка быстро возрастает с ростом (когда становится больше 1). Ясно (как отмечается в [1]), что никакой численный метод не может дать решение этого уравнения с точностью выше 30% при ; эта ошибка уже заложена в исходной информации. Поэтому в [1] такая ошибка называется внутренней неустойчивостью, а мы назвали её неустойчивостью по начальным данным.

В завершение данного подраздела, в качестве второго примера, рассмотрим решение следующей задачи Коши [4]

Она описывает зарядку конденсатора в RC-цепи с приложенным напряжением V. Здесь t – время, измеряемое в секундах; R=2000 Ом – сопротивление; Ф – ёмкость; V= 10 В. Глядя на это уравнение, попробуйте ответить на следующие вопросы: будет ли увеличиваться Q(t) с течением времени; если да, - то увеличение может продолжаться неограниченно или произойдёт насыщение?

Точное решение задачи (1.13) можно записать в виде

В связи с примером (1.13) выполните следующие упражнения:

а) решите задачу (1.13) с приведёнными значениями параметров встроенными средствами пакета Maple;

б) постройте в среде Maple график зависимости , приведённой выше;

в) реализуйте в среде Maple метод Эйлера решения задачи (1.13);

г) реализуйте в среде Maple модифицированный метод Эйлера решения задачи (1.13);

д) сравните на одном рисунке результаты (в форме графиков) выполнения а) и в), на другом рисунке – б) и г);

е) при программировании методов Эйлера (пункты в) и г)) проведите численные эксперименты, увеличивая количество отрезков, на которые разбивается исходный отрезок интегрирования задачи Коши (аналогично первому примеру); можно ли на основании данных экспериментов сделать вывод об устойчивости или неустойчивости метода Эйлера для решения данной задачи Коши?

• Выполните индивидуальное задание: решите задачу Коши из Приложения 1, программируя описанные выше алгоритмы и в среде Maple, и сравните результаты. Как решать задачу, для которой нет ответа в конце учебника, и надеяться на то, что полученное решение - верное? Во-первых, теория методов Рунге-Кутта говорит нам о том, что погрешность приближённого решения должна уменьшаться при уменьшении шага . Следовательно, требуется проводить расчёты с различными значениями . Тогда, если с уменьшением будет сохраняться всё больше значащих цифр в получаемых решениях, то это позволит говорить о правильности получаемого решения.

Во-вторых, следует решать задачу различными методами и сравнивать получаемые решения.

1.6. Методы прогноза и коррекции. Следуя [1], рассмотрим здесь один из эффективных алгоритмов решения задачи Коши, относящийся к числу альтернативных методам Рунге-Кутта. Отличительной чертой методов Рунге-Кутта является то, что при вычислении следующей точки , используется информация только о точке , , но не о предыдущих. В методах второго порядка и выше приходится вычислять значение функции в одной или нескольких промежуточных точках. Это представляется нерациональным, поскольку, если процесс интегрирования уже продвинулся на несколько шагов, то у нас есть эти значения функции на предыдущих шагах. Чтобы начать решение уравнения, имея только одну точку, определяемую начальным условием, или для того, чтобы изменить шаг , необходим метод типа Рунге - Кутта. Поэтому здесь следует использовать разумное сочетание двух методов решения.

Наш метод называется методом прогноза и коррекции. Как ясно из названия, вначале «предсказывается» значение , а затем используется тот или иной метод для «корректировки» этого значения. Естественно, после этого можно использовать ту же самую формулу для вторичной корректировки однажды уже скорректированного значения . Этот итерационный процесс можно повто­рять сколько угодно раз, но оказывается, что из соображений эффективности целесообразно уменьшать число итераций, выбирая должным образом шаг инте­грирования.

Рассмотрим один из вариантов метода. Следуя [1], для прогноза мы используем формулу второго порядка

(1.14)

где верхний индекс (0) означает исходное приближение к , т.е. предсказанное значение. Непосредственно из написания формулы следует, что с ее помощью нельзя вычислить . Это и понятно, так как для вычисления потребовалась бы точка, расположенная перед начальной точкой . Чтобы начать решение с помощью метода прогноза и коррекции, часто используется метод Рунге - Кутта.

Геометрически предсказание сводится к тому, что нахо­дится угол наклона касательной в точке , (прямая на Рис. 3). После этого через точку , проводится прямая , параллельная . Предсказанное значение будет расположено там, где прямая пересечется с ординатой .

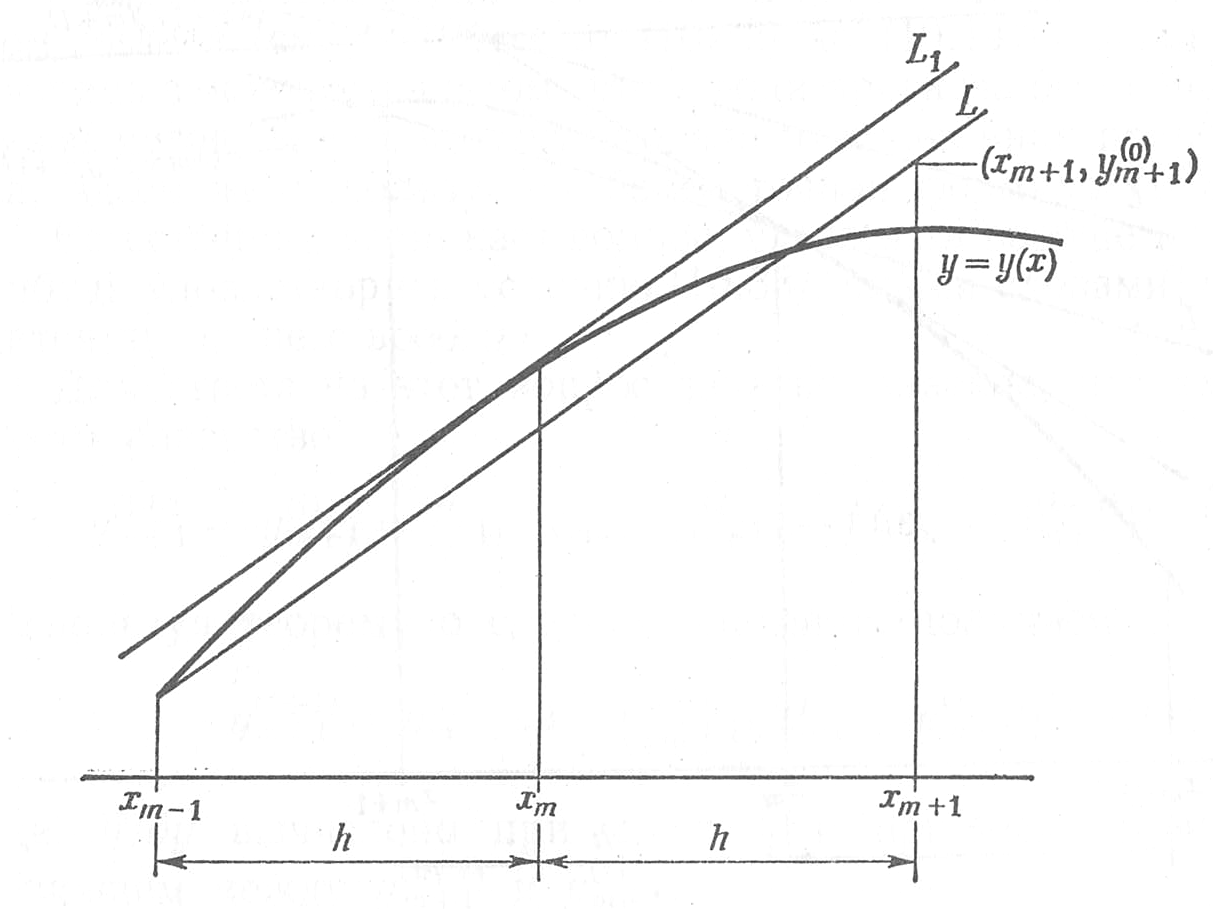
Рис. 3. Геометрическое представление прогнозирующей формулы второго порядка, описанной в тексте.

Теперь требуется некоторый метод коррекции пред­сказанного значения. Так как нам приближенно известна величина , то можно вычислить наклон касательной в точке , . Эта касательная изображена на Рис. 4 и обозначена . Прямая на Рис. 4 пред­ставляет собой то же самое, что и на Рис. 3, и тангенс угла наклона ее равен . Мы усредняем тангенсы углов наклона линий и и получаем линию . Наконец, мы проводим через точку , линию , параллельную и точка пересечения этой линии с ординатой дает новое приближение к значению . Назовем это приближение скорректированным значением .

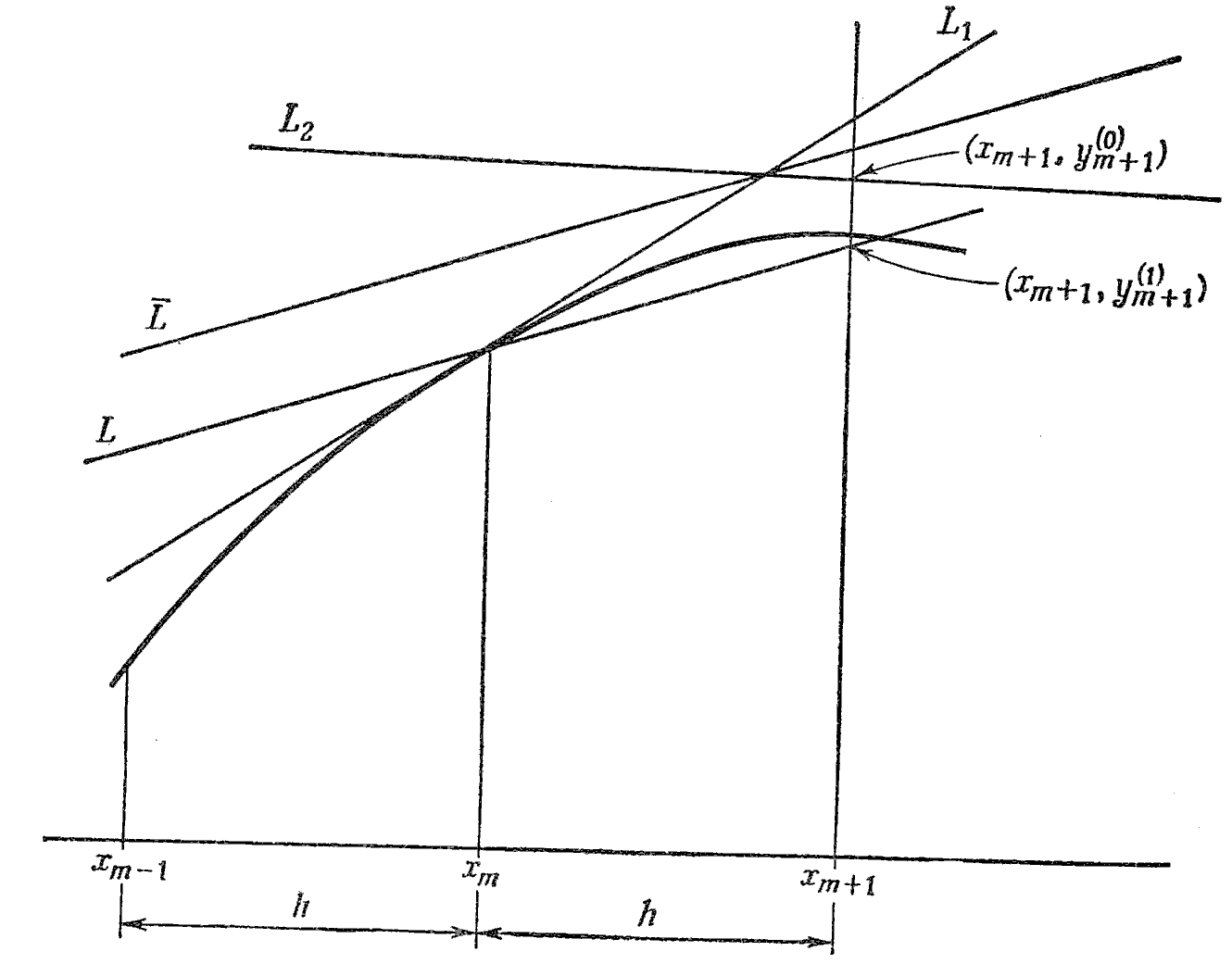
Рис. 4 Геометрическое представление формулы коррекции второго

Вычислить это скорректированное значение можно по формуле

.

Можно найти новое приближение к , используя значение и корректируя снова. В общем случае, i-е приближение к вычисляется по формуле

(1.15)

для . Итерационный процесс прекращается, когда выполняется условие

(1.16)

для некоторого положительного .

Нетрудно показать (следуя [1]), что процесс (1.15), (1.16) сходится. Для этого необходимо потребовать, чтобы производная была ограничена, т.е. можно было найти такую константу , что

и выбрать величину шага из условия

(1.17)

Как выбирать [1]: если его выбрать слишком малым, то для определения каждой точки (т.е. для сходимости процесса (1.15), (1.16)), потребуется мало итераций, но количество точек будет велико; если его выбрать слишком большим, то количество итераций будет велико, зато количество точек будет малым. При программировании важно алгоритм делать оптимальным, т.е. стараться количество его операций минимизировать. В [1] отмечается, что «существуют веские эмпирические соображения, согласно которым оптимальное число итераций равно двум. Под оптимальностью здесь понимается минимальный объём вычислений при заданной точности». Это означает, что при оптимальном значении условие (1.16) удовлетворяется после двух шагов (1.15). Именно этот критерий выбора и нужно запрограммировать: подсчитывается число итераций процесса (1.15), (1.16); если их оказывается больше двух, то текущее значение требуется уменьшить (например, в два раза); если число итераций равно одной, то величину следует увеличить (например, в два раза). Если в результате такой проверки величина изменяется, то весь процесс прогноза-коррекции как бы начинается заново, а именно: полученные значения , следует использовать в качестве «начальных», с этого места применить формулу (1.6) и далее действовать по описанному алгоритму. Можно также показать следующее [1]: после того, как очередное приближение по формулам (1.14), (1.15) в соответствии с описанной процедурой будет найдено, более точное приближение можно найти по формуле

Выражение (1.18) и следует использовать в качестве окончательного значения неизвестной функции на шаге m.

• Запрограммируйте алгоритм прогноза-коррекции на C/C++ или в среде Maple с учётом сделанных замечаний и сравните результаты решения соответствующей задачи Коши с результатами её решения другими методами (сначала решите задачи Коши, рассмотренные выше в качестве примеров, а затем – в соответствии с индивидуальным заданием из Приложения 1).