Производная в данном направлении. Градиент
Производная
функции
в точке
в направлении
,
где
,
определяется соотношением:
,
где
и
-
значения функции
в точках
и
.
Если функция имеет частные производные, то справедлива формула:
,
(5)
где
-
угол, образованный вектором
с осью
.
Аналогично
определяется производная в данном
направлении
для функции трех аргументов
.
В этом случае:
,
(6)
где
-
углы между вектором
и соответствующими координатными осями.
Градиентом функции в точке называется вектор, проекциями которого на координатные оси являются соответствующие частные производные данной функции:
.
(7)
Аналогично определяется градиент функции трех переменных :
.
(8)
Задание 1.
Найти
производную функции
в точке
в направлении вектора
.
Решение. Найдем частные производные данной функции и их значения в точке :
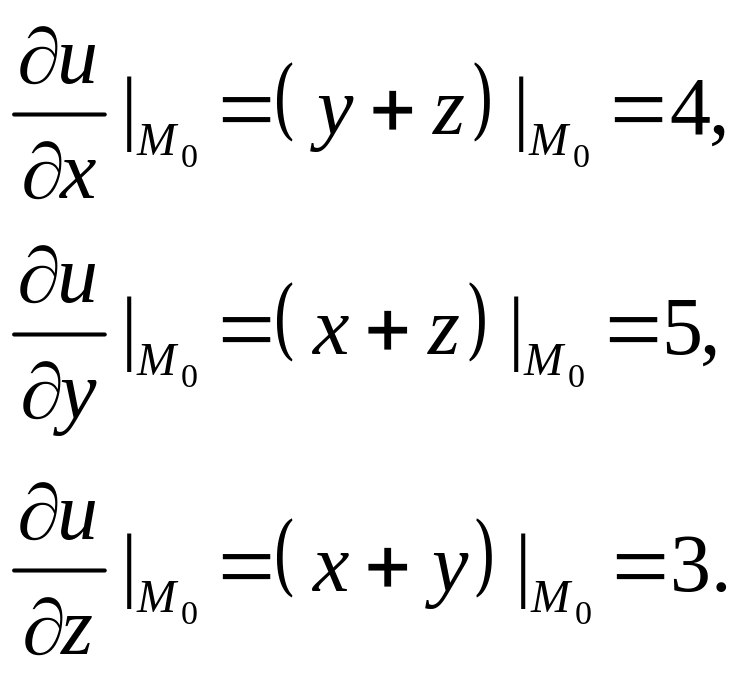
Определим теперь
значения направляющих косинусов вектора
:
.
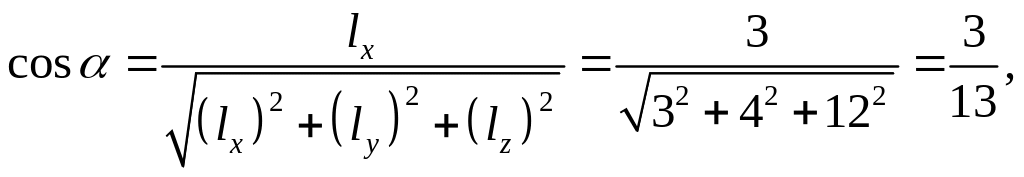
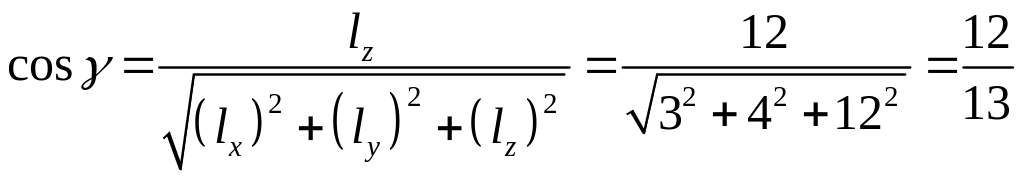Применяя формулу (6), получим:
.
Задание 2.
Для функций
и
найти угол между
и
в данной точке
.
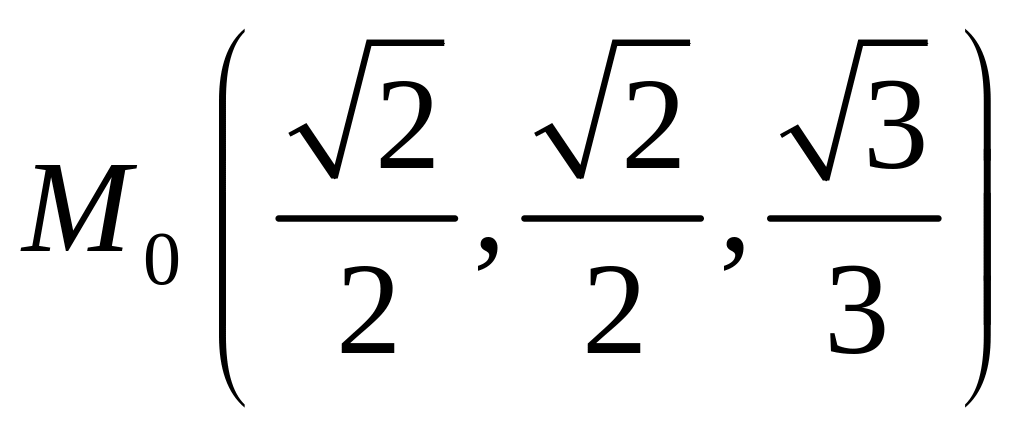Решение. Вычислим частные производные данных функций и их значения в точке :
,
,
,
,
,
.
Тогда в силу формулы (8):
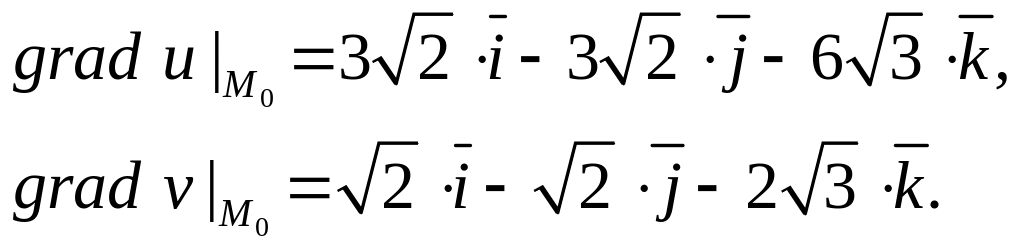
Найдем теперь угол
между градиентами функций. По формуле
для косинуса угла между векторами имеем:
,
Следовательно,
угол между
и
в данной точке
равен
.
5. Касательная плоскость и нормаль к поверхности
Касательной
плоскостью к поверхности
в точке
называется плоскость, в которой лежат
все касательные в точке
к различным кривым, проведенным на
поверхности
через эту
точку.
Нормалью к поверхности в точке называется прямая, перпендикулярная к касательной плоскости, построенной к данной поверхности в точке .
Если уравнение поверхности задано в явном виде
,
где функция
имеет непрерывные частные производные,
то уравнение касательной плоскости к
данной поверхности в точке
имеет вид:
,
(9)
а уравнения нормали -
.
(10)
Если уравнение поверхности задано в неявном виде
,
где функция
имеет непрерывные частные производные,
то уравнение касательной плоскости к
данной поверхности в точке
имеет
вид:
,
(11)
а уравнения нормали -
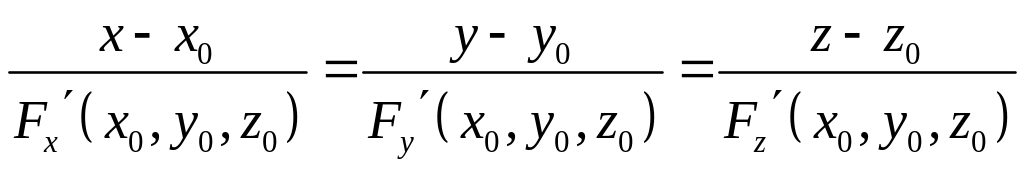(12)
Задание.
Написать
уравнения касательной плоскости и
нормали к поверхности
в точке
.
Решение. Найдем частные производные данной функции и их значения в точке :
.
Применяя формулы (9) и (10), получим:
или
- уравнение касательной плоскости и
или
- уравнения нормали.