Решение:

Найдем уравнение плоскости А1А2А3:	x	y	z–2	= 0
	3	0	3
	-2	1	-5

-3x + 9y +3z – 6 = 0

Итак, А₁А₂А₃: x – 3y – z + 2 = 0.

Нормальный вектор этой плоскости n{1, -3, -1} будет направляющим для искомой прямой. Значит, ее каноническое уравнение имеет вид:

x – 4	=	y – 1	=	z – 2
1		-3		-1

Задача 10. Составьте уравнения плоскостей, отстоящих от плоскости 2x–3y+z–5 =0 на 3.

РЕШЕНИЕ:

1) Точка М(0, 0, 5) принадлежит этой плоскости. Действительно, 2∙0–3∙0+5–5=0. Найдем уравнение прямой L, проходящей через точку М перпендикулярно данной плоскости:

L:	x=2t
	y=-3t
	z=5+t

2) Плоскость, отстоящая от данной на 3 – это плоскость, проходящая через точку А(x₀, y₀, z₀) параллельно данной (нормальный вектор равен {2, -3, 1}), где x₀, y₀, z₀ являются решениями системы:

x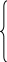 ₀ = 2t₀,

y₀ = -3t₀,

z₀ = 5+t₀,

(4t₀+9t₀+5+t₀-5)²=9∙14

;

3) Плоскость Р₁, проходящая через точку и имеющая нормальный вектор {2, -3, 1}, будет одной из искомых.

Плоскость Р₂ проходящая через точку и имеющая нормальный вектор {2, -3, 1}, также будет искомой.

Ответ: P₁: ; P₂:

Задача 11. В пирамиде с вершинами А₁(1;-2;1), А₂(3;-2;1), А₃(-2;1;0), А₄(2;2;5) найдите:

1. уравнение грани А₁А₂А₃;

2. уравнение плоскости, проходящей через высоту пирамиды, опущенную из вершины А₄ на грань А₁А₂А₃ , и вершину А₁ пирамиды;

3. уравнение прямой, проходящей через вершину А₂ параллельно ребру А₁А₄;

4. точку, симметричную вершине А₄, относительно грани А₁А₂А_3.

РЕШЕНИЕ:

1)

А1А2А3:	x–4	y	z	= 0
	-6	1	2
	4	2	0

–4x + 16 + 8y – 16z = 0

x – 2y + 4z – 4 = 0

2) Найдем уравнение высоты A₄H пирамиды, опущенной из вершины А₄ на грань А₁А₂А₃. Направляющим для нее будет вектор {1, -2, 4}.

A4H:	x=3+t
	y=2–2t
	z=7+4t

Точка М(2, 4, 3) принадлежит этой прямой. Тогда плоскость проходит через точки А₄(3;2;7), М(2, 4, 3) и А₁(4, 0, 0) и ее уравнение будет иметь вид:

x–4	y	z	= 0
3	2	7
2	4	3

-22(x–4) + 5y + 8z = 0

22x – 5y – 8z – 88 = 0

3) Найдем уравнение прямой А₁А₄: . Ее направляющий вектор {-1, 2, 7} будет направляющим и для искомой прямой. Имеем ее каноническое уравнение:

4) Искомая точка принадлежит прямой A₄H и Н= –A₄H.

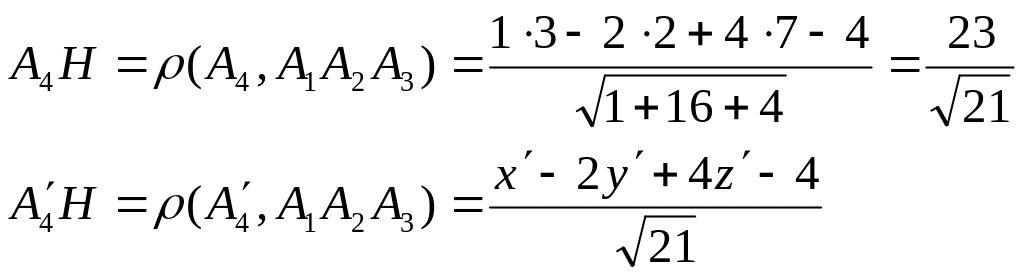
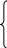
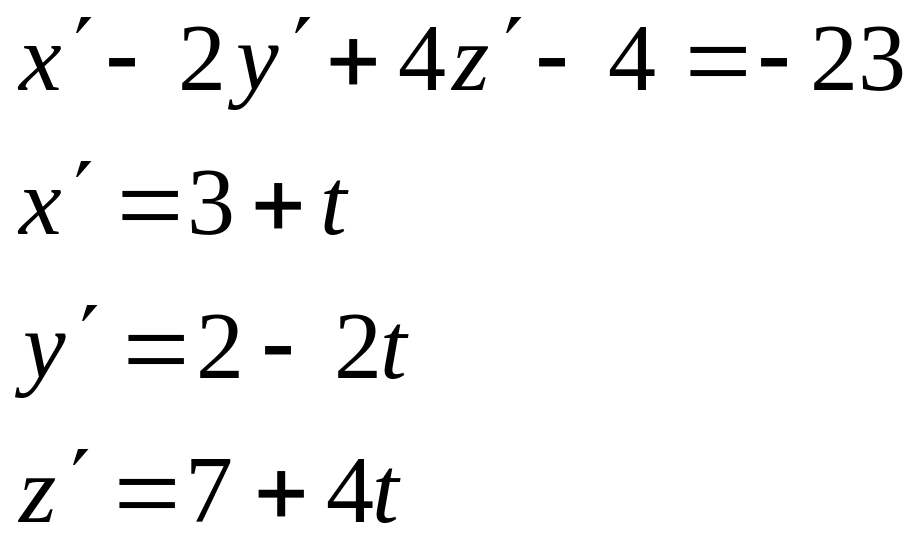
21t+23=–23

Т.е имеет координаты

Ответ: x – 2y + 4z – 4 = 0; 22x – 5y – 8z – 88 = 0; ;

Задача 12. Найти точки пересечения поверхности и прямой:

1+z^2=	x^2	+	y^2
	16		9

y +3 = 0,

x +y -4z +3 = 0.

РЕШЕНИЕ:

1) Найдем параметрическое задание прямой:

q=[n1,n2] =	i	j	k	= -4i+j-k
	0	1	0
	1	1	-4

П усть z₁=2, то y = -3

x + y = 5

y = -3

x = 8

Точка А(8, -3, 2) принадлежит прямой. Тогда прямую можно задать следующим образом:

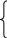x = 8 - 4t

y = –3 + t

z = 2 - t

2) Пусть М(x₀, y₀, z₀) – точка пересечения прямой и плоскости, тогда:

x₀ = 4(2-t₀),

y₀ = -3+t₀,

z₀ = 2-t₀,

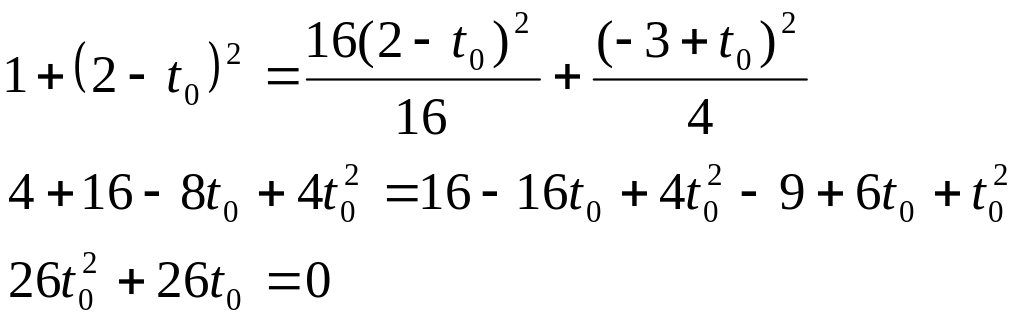
t₀=6,5 или t₀= –4,5

Имеем: M₁(8, -3, 2) и М₂(-18, 3,5, -4,5).

Ответ: M₁(8, -3, 2) и М₂(-18, 3,5, -4,5).