Лекція 4 Композиції машин т'юрінга

З математичної точки зору машина Т'юрінга - просто певний алгоритм для переробки слів.

Операції композиції, виконувані над алгоритмами, дозволяють утворювати нові, більше складні алгоритми з раніше відомих простих алгоритмів. Оскільки машина Т'юрінга - алгоритм, то операції композиції застосовні й до машин Т'юрінга. Розглянемо основні з них, а саме: добуток, зведення в ступінь, ітерацію.

Нехай задані машини Т'юрінга T₁ і Т₂, що мають якийсь загальний зовнішній алфавіт А = {а₀, a₁, ..., а_m} і внутрішні алфавіти Q₁ = {q₀, q₁, .., qn} і відповідно Q₂ = {q’₀, q’₁ , ..., q'_t). Композитом, або добутком, машини Т₁ на машину Т₂ будемо називати машину Т с тим же зовнішнім алфавітом А = {а₀, a₁, ..., а_m}, внутрішнім алфавітом Q= {q₀, q₁, ..., q_n, q_n+1, ..., q_n+t } і програмою, що виходить наступним чином. У всіх командах Т₁, що містять заключний символ q₀, заміняємо його на символ q_n+i. Всі інші символи в командах Т₁ залишаємо незмінними. У командах Т₂, навпроти, символ q₀ залишаємо незмінним, але зате кожний з інших символів q_j¹(j = 1, 2, ..., t) заміняємо символом q_n+j. Сукупність всіх команд T₁ і Т₂, змінених зазначеним способом, і буде, програмою композита або добутку машин T₁ и T₂.

Добуток машини Т₁ на машину Т₂ позначається через Т = Т₁ ^. T₂, або Т = Ti * T₂.

Таким чином, машина Т є добуток машин T₁ і Т₂, якщо послідовна робота цих двох машин еквівалентна роботі однієї машини T.

Таблиця відповідності такої машини будується за наступним правилом: якщо керуючий пристрій машин T₁ і Т₂ мають k₁ й k₂ станів відповідно (без урахування заключних станів), то керуючий пристрій машини Т має k₁ + k₂ станів, причому початковим станом машини Т є q₁¹ (початковий стан T₁), а заключним — q₀² (заключний стан машини Т₂). Таблиця відповідності машини Т складається із двох частин: верхня описує машину T₁, нижня — машину T₂. При цьому заключний стан машини T₁ ототожнюється з початковим станом машини Т₂.

Нехай машина T₁ задана таблицею відповідності:

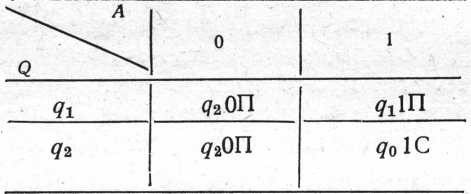
Ця машина відшукує найближчу ліворуч групу одиниць після групи нулів.

Машина Т₂ задана таблицею відповідності:

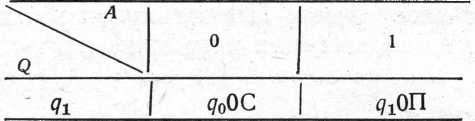
Машина стирає всі одиниці ліворуч, якщо вони є, до найближчого ліворуч нуля.

У вихідному стані головки, що зчитують, машин T₁ і Т₂ перебувають у крайньої правої заповненої комірки. Тоді, машина T, що є їхнім добутком, буде мати таблицю з 2+1=3 станами, q₀ = q₀² — заключний стан машини Т₂:

Якщо для машини Т застосувати нову нумерацію станів, то таблиця відповідності прийме вид:

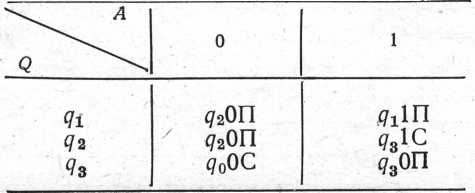
Машина Т відшукує найближчу групу одиниць і стирає їх.

У такий же спосіб визначається операція зведення в ступінь: п-й ступенем машини Т називається добуток T... Т с п співмножниками.

У тому випадку, коли одна з машин, що перемножують, має два або кілька заключних станів, множення визначається зовсім аналогічно, але тільки обов'язково повинна бути присутня вказівка, яке із заключних станів попереднього співмножника ототожнюється з початковим станом наступного.

Так, наприклад, якщо машина Т₁ має два заключних стани, то добуток Т₁ й T₂ будемо позначати через

T=T₁ або T=T₁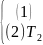

з алежно від того, чи ототожнюється початковий стан машини T₂ з першим або із другим заключним станом машини T₁.

Машина Т у цьому випадку також має два заключних стани: перше — один із заключних станів машини T₁, друге — заключний стан T₂.

У прикладі

T=T₁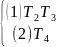

множення провадиться незалежно по двох каналах, пов'язаним з першими й другим заключними станами машини T₁.

Операція ітерації застосовна до однієї машини.

Суть цієї операції полягає в наступному. Нехай машина Т₁ має кілька заключних станів. Виберемо яке-небудь r-тий заключний стан й ототожнимо його в основній таблиці машини T₁ з її початковим станом. Отримана машина позначається через

T=T1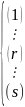

і є результатом, ітерацій машини T₁. Тут крапка вказує на ототожнення заключного стану з початковим станом машини T₁.

Якщо T₁ має тільки один заключний стан, то після виконання ітерації виходить машина, що не має заключного стану зовсім.

Якщо ітерація провадиться над машиною, що сама є результатом множення й ітерації інших машин, то відповідне число крапок ставиться над тими машинами, чиї заключні й початкові стани ототожнюються.

Наприклад, запис

T=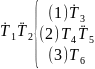

означає, що заключний стан Т₃ ототожнюється з початковим станом T₁, а заключний стан T₅ ототожнюється з початковим станом T₂.

Розглянемо приклад побудови машини за допомогою операцій множення й ітерації.

Нехай вихідними є машина T₂, розглянута в композиції добутку машин, і машини T₃, Т₄ і Т₅, що мають наступні таблиці відповідності.

Машина Т₃:

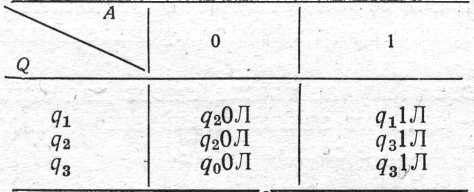
Машина відшукує першу після групи нулів групу одиниць праворуч від початкової комірки й зупиняється біля останньої із цих одиниць.

Машина T₄:

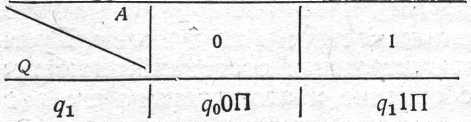
Починаючи роботу із заповненої комірки, машина T₄ іде ліворуч і зупиняється лівіше групи одиниць на дві комірки.

Машина Т₅:

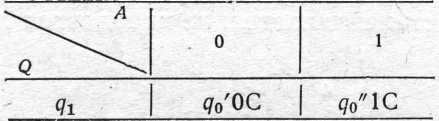
Маючи два заключних стани — q₀' й q₀" машина «розпізнає», напроти якого осередку перебуває зчитуюча голівка, і залежно від цього переходить у перший або другий заключний стан.

Тоді машина, обумовлена формулою

Т=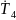 T₅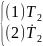

має наступну таблицю відповідності:

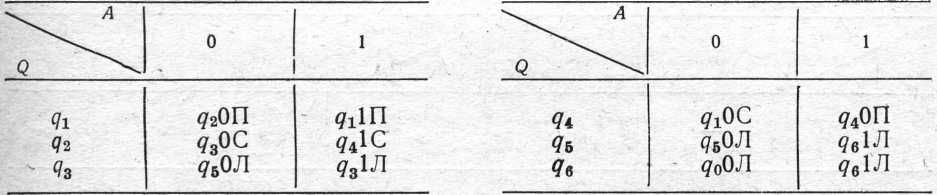
Машина N, перебуваючи в початковий момент часу в стані q₁, напроти заповненої комірки стирає всі одиниці ліворуч від початкового положення до того місця, де вперше зустрічаються два порожні комірки підряд. Після цього стрічка машини повертається назад і зупиняється в крайньій правій заповненій комірки тієї групи розташованих підряд одиниць, з якої машина починала працювати. Машина повторює операцію «стирання» груп одиниць доти, поки лівіше деякої групи одиниць не виявляться два порожні комірки. Таким чином, застосування операції ітерації дозволяє складати машини, що повторюють певну послідовність операцій на стрічці.

Перш ніж розглянути інші приклади композицій машин Т'юрінга, приведемо ряд машин, з яких будуть будуватися ці композиції.

Машина Т₆:

Якщо в початковий момент машина перебуває в стані q₁ і головка, що зчитує, перебуває над коміркою, у якій записа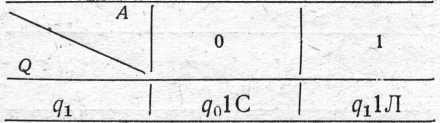

на «1», то вона «відшукує» на стрічці першупорожню комірку, тобто комірку з нулем праворуч від тієї, над якою перебуває голівка, записує в ній «1» і зупиняється. Якщо ж що спочатку зчитуюча голівка перебувала напроти порожньої комірки, то машина записує в ній «1» зупиняється, не пересуваючи стрічки.

Машина Т₇:

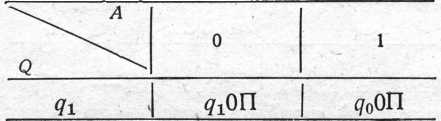
Ця машина «стирає» одиницю в тій комірці, де перебуває голівка, якщо комірка не порожня, пересуває стрічку вправо на одну комірку і зупиняється. Якщо голівка в початковий момент часу перебувала над порожньою коміркою, то стрічка пересувається вправо доти, поки не опиниться над коміркою, що містить «I», і працює так, як описано вище.

Машина Т₈:

Машина заповнює перший проміжок праворуч між двома групами одиниць, залишаючи всього одну незаповнену комірку.

Машина Т₉ має два заключних стани q₀'— і q₀":

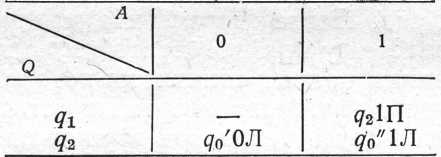
Вона заносить одиницю ліворуч від групи одиниць через одну порожню комірку.

Перебуваючи в початковому стані завжди проти заповненої комірки, машина виявляє, що записано в сусідній комірці ліворуч: 0 або 1. Залежно від цього вона переходить у стан q₀' або q₀" і зупиняється у початковійкомірці.

Мишина Т₁₀:

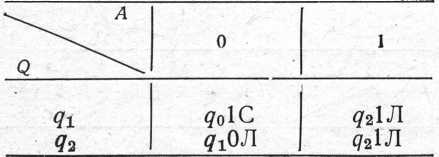
Машина T₁₁:

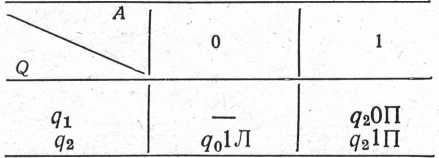
Починаючи роботу із заповненої комірки, машина стирає в ній одиницю й «переносить» її в найближчу порожню комірку ліворуч.

Машина T₁₂:

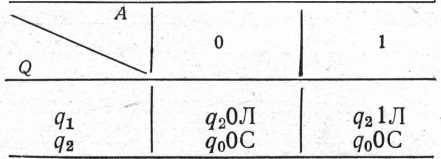
Машина стирає одну одиницю в комірці, розташованій правіше початкової (якщо там є «I»).

Розглянемо приклад побудови машини Р з машин T₃, T₅, T_б, Т₁₁, T₁₂ за допомогою композицій ітерації й добутки по наступній формулі:

P=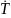 ₁₁T₅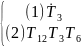

Машина Р починає роботу, сприймаючи саму праву заповнену комірку представлення якого-небудь числа. Результатом її роботи є ситуація, у якій це число «переганяється» ліворуч і ставиться поруч із найближчим ліворуч числом.

До такого ж результату може привести машина з більш простою таблицею відповідності:

С

Машина R_т строится из машин T₁, Т₃ T₆, Т₇, Т₈, Т₉, Т_і0 по формуле

где т — степень соответствующей машины.

В частности,

приймаючи в початковий момент часу систему чисел x₁, ..., х_т у стандартному положенні, машина R_т друкує праворуч від подання чисел x₁, ..., х_m перше із цих чисел (тобто x₁) і зупиняється, сприймаючи в стандартному положенні систему m + 1 чисел (х₁, ..., x_т, x₁). Якщо ж машина R_m сприймає в початковий момент часу в стандартному положенні систему чисел х₁, ..., х_п, де п> т, то вона віддруковує праворуч від цієї системи чисел число хn-т + 1 і зупиниться, сприймаючи систему (x₁, x₂, …, x_n, x_n-m+1)...

Легко можна переконатися, що т-я ступінь машини R_m — R_m^m копіює систему чисел (х₁, ..., x_m), сприйняту в стандартному положенні праворуч так, що результатом роботи буде система 2т чисел (х₁,…, х_т, х₁, ..., х_т), розділених одним проміжком.

Якщо початкова конфігурація 0011110000, те, заключна - 001111011110000.

Машина S_m будується по формулі:

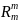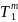S_m=T₆ T₇ T₇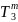

Машина S_m робить майже те ж, що й машина R_m^m, тобто копіює систему чисел (х₁, …, х_т) праворуч, але не з одним проміжком, а із двома (тобто між числами х_m й x₁ розташовані дві порожні комірки).

Нехай є система чисел (х₁, x₂), де x₁ = 2, х₂ = 4. Тоді якщо початкова конфігурація була 011011110000, то скінченна конфігурація буде мати вигляд: 01101111001101111000.

Умовимося тепер, як будуть записуватися й зчитуватися зі стрічки аргументи й значення функцій, що обчислюються. Будемо говорити, що зчитуюча й записуюча голівка сприймає систему чисел (х₁, ..., х_т) у стандартному положенні, якщо, по-перше, ці числа записані підряд й, по-друге, голівка розташована напроти самої правої комірки в представлень останнього із чисел (х_п).

Дамо визначення поняттю обчислення на машині Т'юрінга. Нехай задана машина T і нехай у початковий момент часу виконані наступні умови:

1. машина Т перебуває в початковому стані q₁;

2. на стрічці представлена система п чисел (х₁, …, х_п), яку голівка сприймає в стандартному положенні;

3) всі осередки, розташовані правіше тієї, напроти якої перебуває голівка, порожні.

Будемо вважати, що T обчислює функцію x=φ(x₁, …, x_n) від п змінних, якщо які б не були числа х₁,…,х_п існує такий момент часу, у який:

1) машина Т досягає заключного стану q₀;

2. на стрічці буде представлена система п + 1 чисел х₁, … х_п, х, де х = φ (х₁, х_п), що голівка машини сприймає в стандартному положенні;

3. всі комірки, розташовані правіше тієї, напроти якої перебуває голівка, порожні.

Якщо ж для якої-небудь системи чисел (х₁, ..., х_п) машина ніколи не зупиняється або зупиняється, але при цьому не виконано 2 або 3 умова, то така машина не обчислює значення функції φ при цих значеннях аргументів.

Розглянемо приклад. Нехай п = 3, φ (x₁, х₂, х₃) = х₁ + x₂ + х₃. Тоді при x₁ = 3, x₂ = 3, x₃ = 4 початкова конфігурація на стрічці буде мати вигляд 00 111 0 11 0 1111 0, а заключна ситуація запишеться так 00 111 0 11 0 1111 0 1111111110. Зчитуюча голівка, при цьому розташована над крайньою правою одиницею.

Розглянемо машини Т'юрінга, що обчислюють елементарні арифметичні функції, з яких будуються рекурсивні функції.

Функцію безпосереднього проходження S(x) =х + 1 обчислює машина Т = R₁T₆. Дійсно, сприймаючи в початковий момент число х у стандартному положенні, машина запише S(x) = х + 1 правіше числа х і зупиниться в стандартному положенні (х, х + 1), тобто обчислить функцію безпосереднього проходження.

Константну функцію О^п(х₁,…, х_п) = q обчислює машина Т = Т₁₀Т₆^q, що правіше системи чисел (x₁, ..., х_п) записує q і зупиняється.

Тотожну функцію I_iⁿ(x₁,…, x_п) = x_i обчислює машина Т=R_n-i+1. Дійсно, ця машина правіше системи чисел (х₁, ..., х_п) записує (п — i + 1) -е число, тобто Х_i.

Можна довести, що будь-яка рекурсивна функція може бути обчислена на машині Т'юрінга й навпаки, що на машині Т'юрінга обчислюються тільки рекурсивні функції.

Має місце наступна теорема Т'юрінга (1). Для кожної частково рекурсивної словникової функції f(x₁, ...,x_g), певної в деякому алфавіті а₁ , ..., а_m існує машина Т'юрінга із символами a₀, a₁, ..., а_m і підходящими внутрішніми станами, що обчислює функцію f(x₁, ..., x_g).

Кожна частково рекурсивна функція виходить із найпростіших арифметичних функцій за допомогою операцій суперпозиції, примітивній рекурсії й мінімізації. Тому теорема Т'юрінга буде доведена, якщо нам вдасться вирішити наступні часткові задачі:

1. Побудувати машини Т'юрінга, що обчислюють найпростіші арифметичні функції.

2. Маючи машини Т'юрінга, що обчислюють функції f, f₁, …, f_s, побудувати машину, що обчислює суперпозицію цих функцій.

3. Маючи машини Т'юрінга, що обчислюють якісь функції g й h побудувати машину, що обчислює функцію, що виникає з g й h примітивною рекурсією.

4. Побудувати машину Т'юрінга, що здійснює обіг функції.

Перша із цих задач нами вже вирішена, інші пропонується вирішити читачеві.

Вправи:

1. Машина Т'юрінга задана зовнішнім алфавітом А = {0, 1,*}, внутрішнім алфавітом Q = {q₀, q₁, q₂, q₃}, де 0 -порожній символ, а q₃ — заключний стан. Програма машини Т'юрінга задана у вигляді наступної таблиці відповідності:

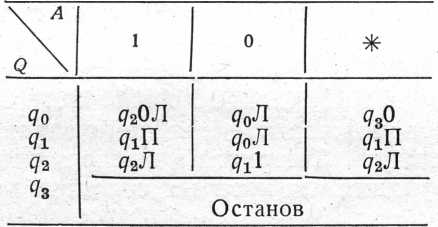
Записати алгоритм додавання двох чисел із вказівкою проти кожної команди відповідних конфігурацій, заданих на стрічці у вигляді:

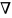q₀

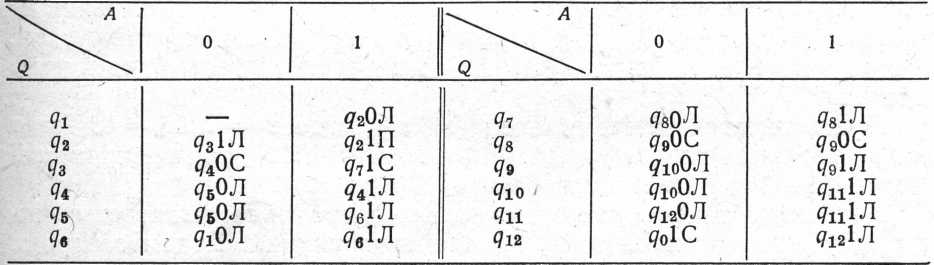
2. Задано машину Т'юрінга:

А = {0,1}, Q = {q₀, q₁, q₂, q₃, q₄, q₅, q₆, q₇, q₈, q₉, q₁₀, q₁₁, q₁₂},

де 0 — порожній символ, а q₁₂— заключний стан.

Програма задана у вигляді:

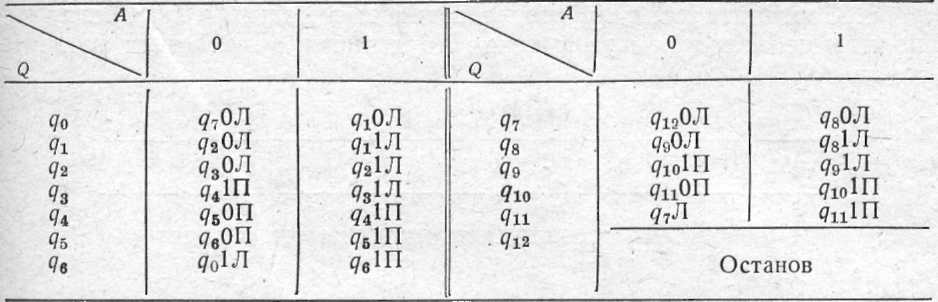
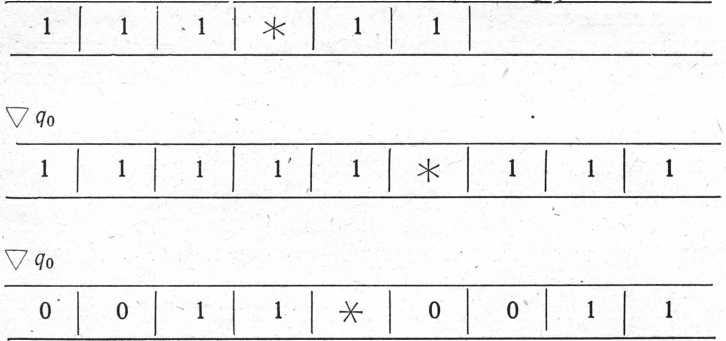
Записати алгоритм додавання чисел, заданих на стрічці у вигляді

1

1

1

1

1

0

1

1

1

Машина починає перегляд із самої лівої одиниці, перебуваючи в стані q₀.

Результат підсумовування повинен бути представлений у вигляді

1

1

1

1

1

0

1

1

1

0

1

1

1

1

1

1

1

1

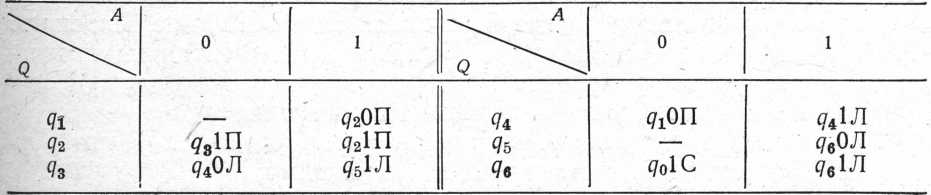
3. Машина Т'юрінга задана наступною таблицею:

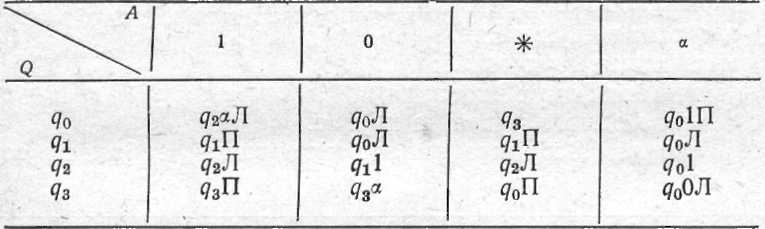
Записати алгоритм повторного додавання чисел тип, заданих у вигляді

Процес додавання полягає в наступному: ліве число т додається до першого числа п, потім т додається до отриманої суми п + т и т.д.

Перегляд стрічки починається із самої лівої одиниці. Машина перебуває в стані q₀.

4. Скласти таблицю відповідності для машини Т'юрінга, що виконує алгоритм множення двох чисел, і записати алгоритм. За основу взяти таблицю відповідності для повторного додавання (3 вправа) і змінити її так, щоб процес повторного підсумовування виконувався стільки разів, скільки одиниць у множнику, після чого треба зупинити машини.

5. Скласти таблицю відповідності для машини Т'юрінга, що виконує алгоритм множення двох чисел, записаних на стрічці у вигляді

q₃

1

1

1

•

1

1

*

1

1

Результат множення повинен бути представлений у вигляді:

Записати алгоритм із вказівкою відповідних конфігурацій.

6. Скласти таблицю відповідності для машини Т'юрінга, що виконує алгоритм множення двох чисел.

Записати алгоритм із вказівкою для кожної команди відповідної конфігурації.

7. Скласти таблицю відповідності для машини Т'юрінга, що виконує алгоритм віднімання, записати алгоритм і відповідній кожній команді конфігурації.

8. Скласти таблицю відповідності для машини Т'юрінга, що виконує алгоритм ділення, записати алгоритм із відповідними конфігураціями.

9. Користуючись поняттям машини Поста, записати алгоритми:

а) додавання двох чисел;

б) вирахування двох чисел;

в) множення двох чисел;

г) ділення одного числа на інше.

10. Машина Т'юрінга задана наступною таблицею відповідності:

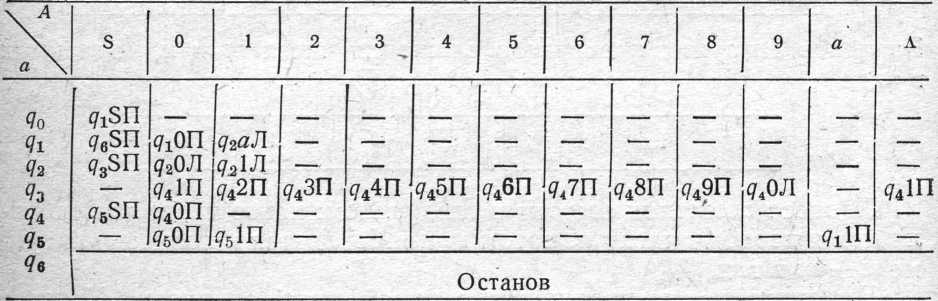
Записати алгоритм лічильника одиниць із вказівкою відповідних конфігурацій.

11. Скласти таблицю відповідності для машини Т'юрінга, що виконує алгоритми додавання й віднімання. Записати алгоритм одного приклада із вказівкою конфігурацій, що відповідають кожній команді.

12. Скласти таблицю відповідності для машини Т'юрінга, що виконує алгоритми додавання, віднімання, множення, ділення. Записати алгоритм одного із прикладів із вказівкою відповідних конфігурацій.