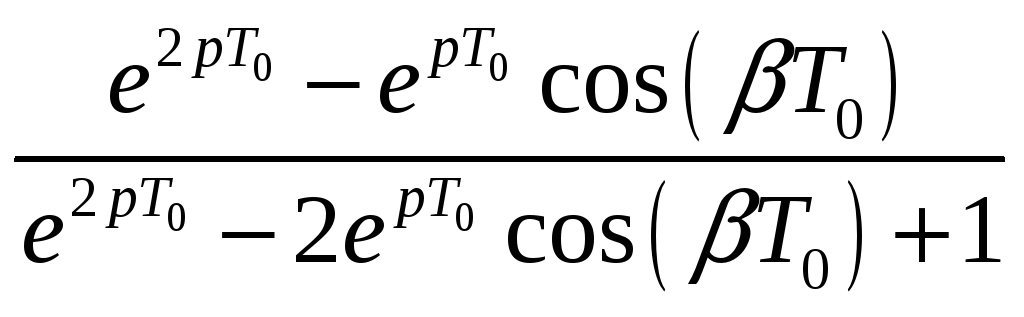Лабораторная работа №2. Вариант №4

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФИЛИАЛ В Г. ИШИМБАЙ

Кафедра Автоматизации Производственных Процессов

Отчет по лабораторной работе №2

по предмету «Теория автоматического управления»

на тему: Исследование импульсной САУ.

Выполнил: студент гр. АТП-308

Шарипов Д.В.

Принял: Хуснутдинов Д.З.

Ишимбай 2007

1. Цель работы

Исследование импульсных систем автоматического управления; изучение влияния параметров непрерывной части системы и периода квантования на характеристики импульсной системы.

2. Выполнение работы

Задание №4

; k=90; T²=10 с²; T₀=0.166 c

1. Сформировать структурную схему замкнутой импульсной САУ или привести ее к виду:

В качестве формирующего звена использовать фиксатор нулевого порядка с передаточной функцией .

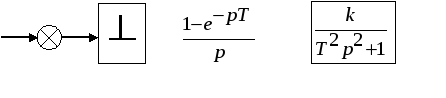
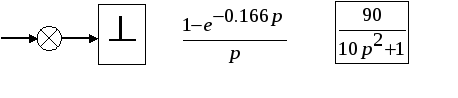
2. Проанализировать устойчивость линейной части системы.

Непрерывная линейная часть имеет передаточную функцию , т.е. представляет собой консервативное звено. Как известно, переходная функция данного звена представляет собой незатухающие гармонические колебания. Построим переходную функцию непрерывной линейной части импульсной системы, используя Control System ToolBox пакета Matlab:

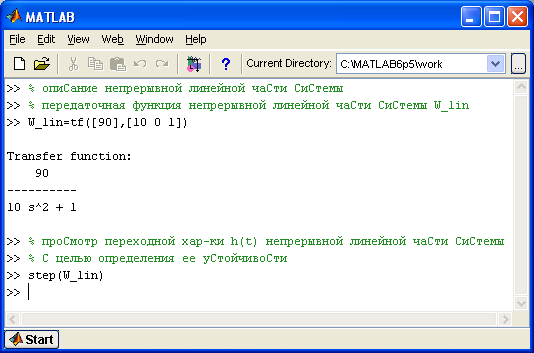
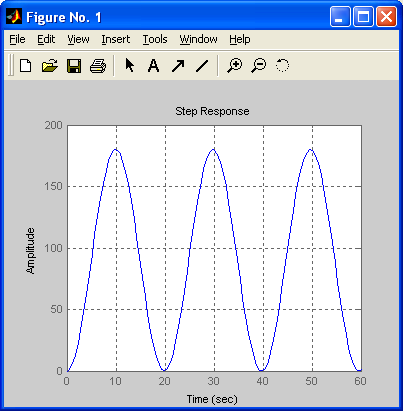
Как видно из графика, переходная функция данного звена представляет собой незатухающие гармонические колебания с постоянной амплитудой. Это означает, что непрерывная линейная часть импульсной системы находиться на границе устойчивости.

3. При заданных коэффициентах передаточной функции линейной части системы и заданном периоде дискредитации найти передаточную функцию замкнутой импульсной системы.

Для удобства анализа системы объединим формирующий элемент и непрерывную линейную часть импульсной системы. В результате получим эквивалентную расчетную схему, состоящей из простейшего импульсного элемента и приведенной непрерывной части:

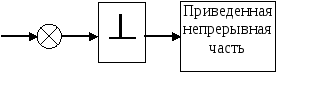
Передаточная функция приведенной непрерывной части имеет вид:

(2.1)

Так как в качестве формирующего элемента используется фиксатор нулевого уровня с передаточной функцией , то передаточная функция приведенной непрерывной части импульсной системы примет вид:

(2.2)

Используя дискретное преобразование Лапласа, найдем передаточную функцию разомкнутой импульсной системы:

(2.3)

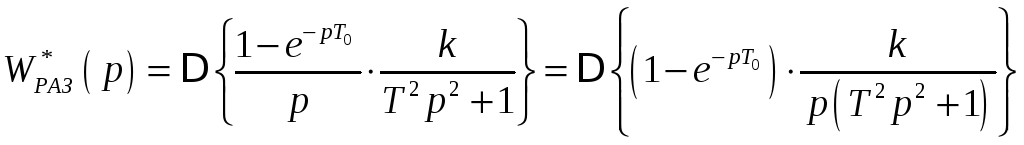(2.4)

Воспользовавшись теоремой умножения изображений непрерывной и решетчатой функций

выносим в формуле (2.4) за знак -преобразования функции от :

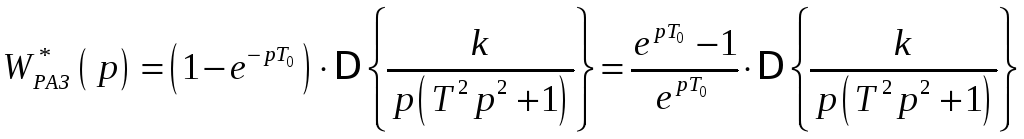(2.5)

Для нахождения дискретного преобразования Лапласа 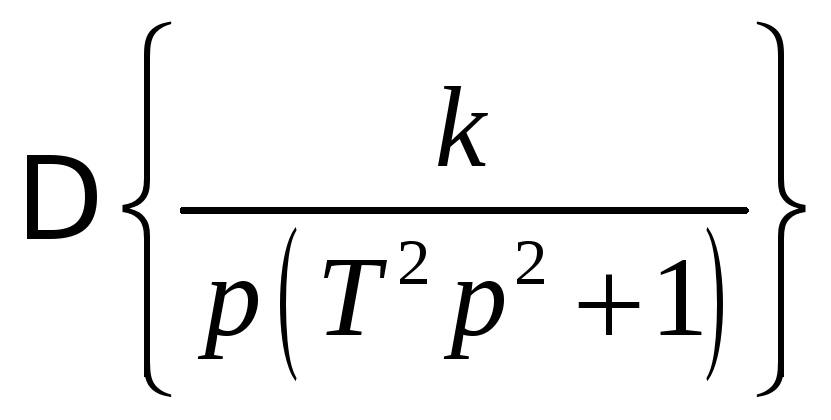дробно-рациональную функцию под знаком -преобразования разложим на сумму простых дробей и, воспользовавшись таблицей изображений решетчатых функций, найдем изображения для каждого слагаемого.

Воспользуемся методом неопределенных коэффициентов:

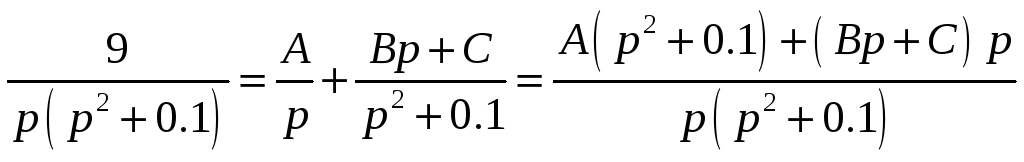
Согласно таблице изображений решетчатых функций

Производящая непрерывная функция		D-преобразование
оригинал	преобразование Лапласа

получим:

(2.6)

Подставляя (2.6) в (2.5), получим передаточную функцию разомкнутой импульсной системы:

Произведя замену переменной , получим z-преобразование:

(2.8)

Передаточную функцию разомкнутой импульсной системы можно найти с помощью Control System Toolbox пакета MatLab:

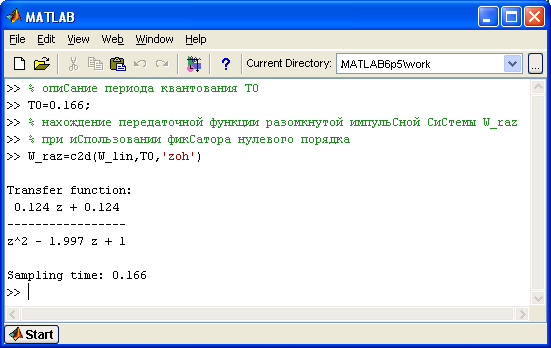
Передаточная функция замкнутой импульсной системы примет вид:

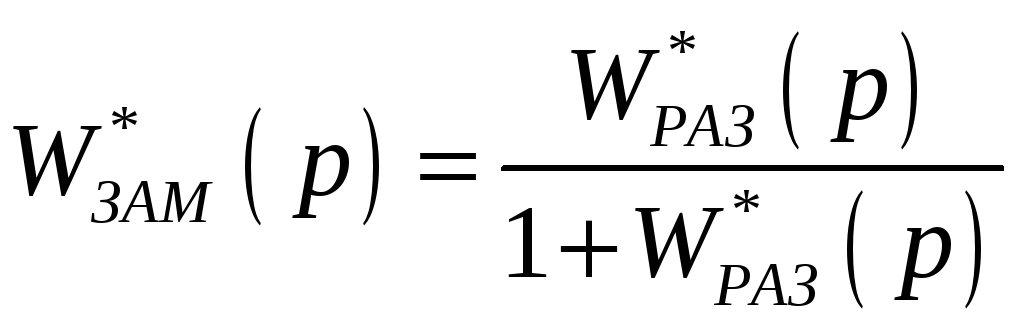
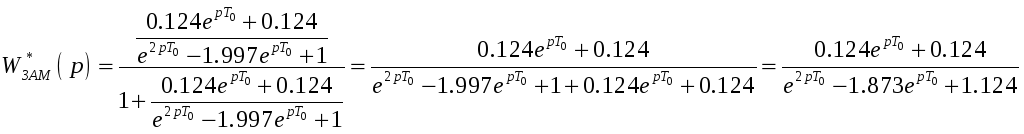(2.9)

или в -форме

(2.10)

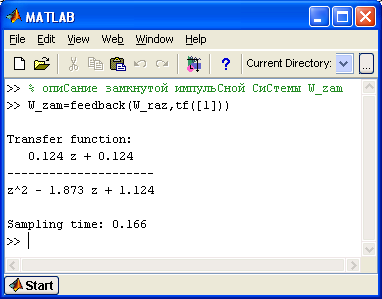
Тот же самый результат можно получить при помощи Control System Toolbox пакета MatLab.

4. С помощью пакета прикладных программ составить на экране компьютера структурную схему замкнутой импульсной САУ. Получить график переходного процесса.

Для составления структурной схемы и моделирования импульсной системы воспользуемся пакетом Simulink, входящий в состав пакета MatLab.

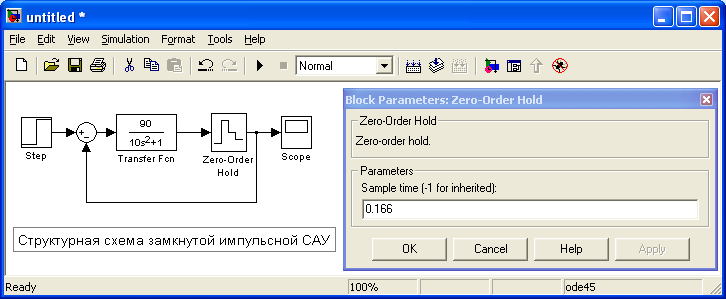
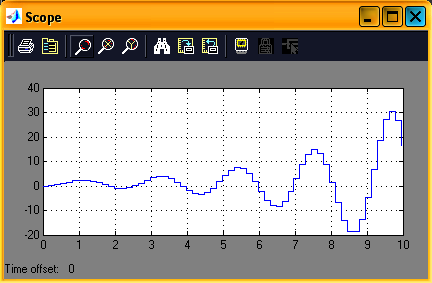
График переходного процесса

График переходного процесса может быть получен с помощью Control System Toolbox пакета MatLab.

5. Разомкнуть внешнюю обратную связь и получить амплитудно-фазовую характеристику . С помощью частотных критериев оценить устойчивость импульсной системы.

Для того, чтобы получить амплитудно-фазовую характеристику разомкнутой импульсной системы, воспользуемся Control System Toolbox пакета MatLab:

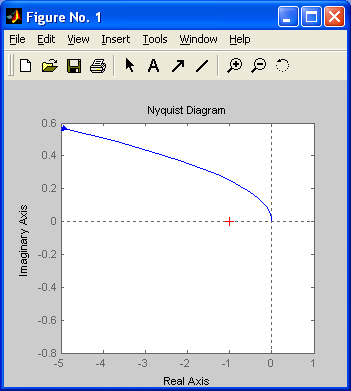
Как видно из графика амплитудно-фазовая характеристика разомкнутой импульсной системы охватывает точку с координатами (-1; j0). Согласно критерию устойчивости Найквиста, это означает, что замкнутая импульсная система будет неустойчивой, что подтверждается графиками переходного процесса, приведенными выше.

Как известно, об устойчивости замкнутой импульсной системы можно судить по расположению полюсов ее передаточной функции в плоскости z относительно окружности единичного радиуса. Условием устойчивости будет нахождение полюсов передаточной функции замкнутой импульсной системы внутри этой окружности. Воспользуемся Control System Toolbox пакета MatLab для того, чтобы оценить расположение корней передаточной функции замкнутой импульсной системы относительно окружности единичного радиуса в плоскости z.

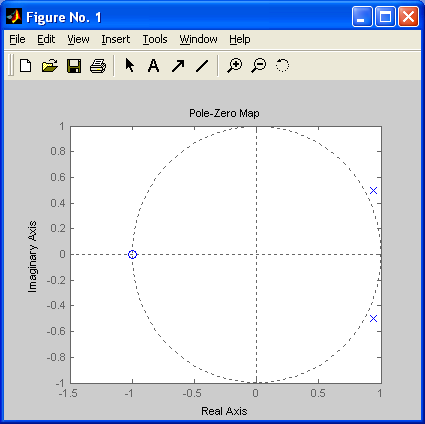
Как видно из графика, имеются два полюса, которые не лежат внутри окружности единичного радиуса. Следовательно, замкнутая импульсная система является неустойчивой.

6. Исследовать влияние на устойчивость и качество процесса регулирования изменения периода дискредитации и общего коэффициента передачи системы.

Для исследования влияния на устойчивость периода дискредитации и общего коэффициента передачи системы k запишем характеристический полином (знаменатель передаточной функции замкнутой импульсной системы (2.10)) в общем виде при помощи z-преобразования:

(2.11)

Тогда характеристическое уравнение примет вид:

(2.12)

Выпишем коэффициенты характеристического уравнения (2.12):

Для исследования влияния на устойчивость периода дискредитации и общего коэффициента передачи системы k воспользуемся алгебраическим критерием устойчивости Гурвица. Для этого необходимо осуществить -преобразование, т.е. произвести замену переменной

(2.13)

Осуществим -преобразование для характеристического уравнения (2.12):

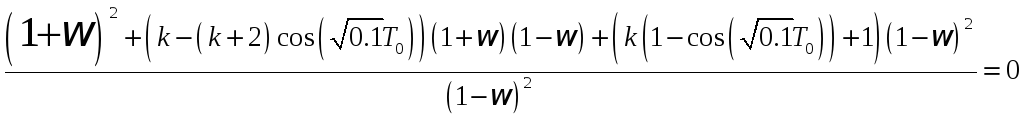
(2.14)

После раскрытия скобок и приведения подобных членов, характеристическое уравнение (2.14) примет вид:

(2.15)

Выражения для коэффициентов характеристического (2.15) через коэффициенты исходного характеристического уравнения (2.12) для систем второго порядка имеют вид:

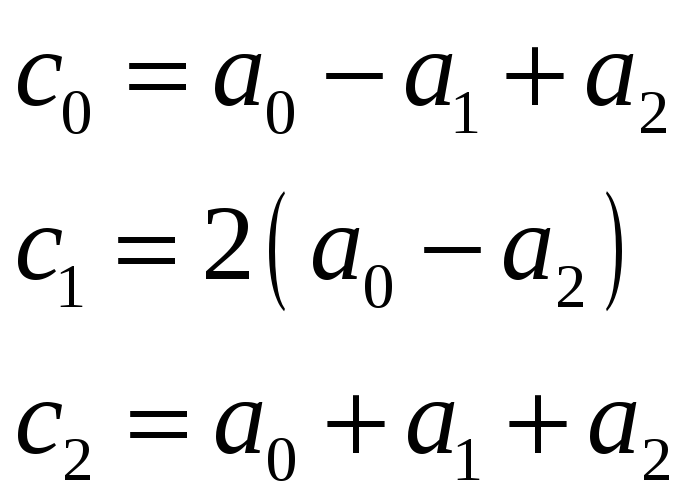
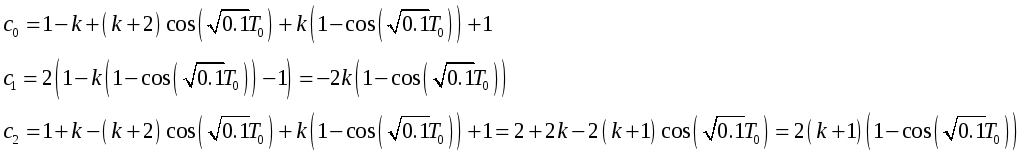
Далее, согласно алгебраическому критерию Гурвица, из найденных коэффициентов нужно составить квадратную матрицу:

Замкнутая импульсная система будет устойчивой, если

Подставим найденные выражения для коэффициентов :

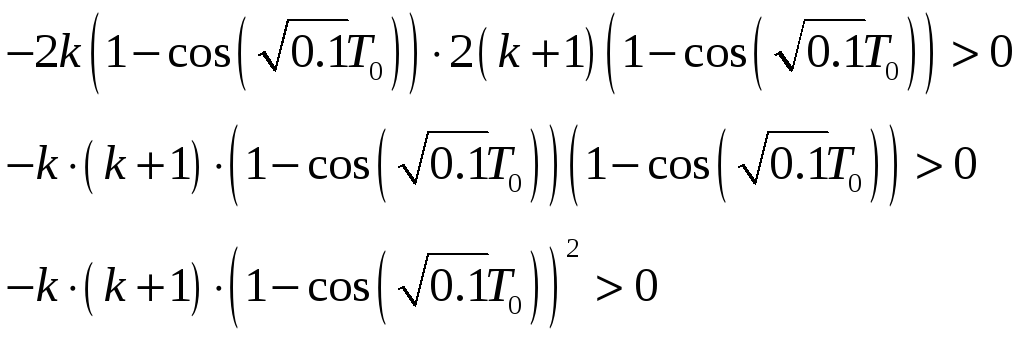
Как видно из последнего неравенства при любом положительном значении общего коэффициента передачи системы k замкнутая импульсная система будет неустойчивой. Однако, можно добиться того, чтобы исследуемая система находилась на границе устойчивости. Для этого необходимо, чтобы выполнялось условие

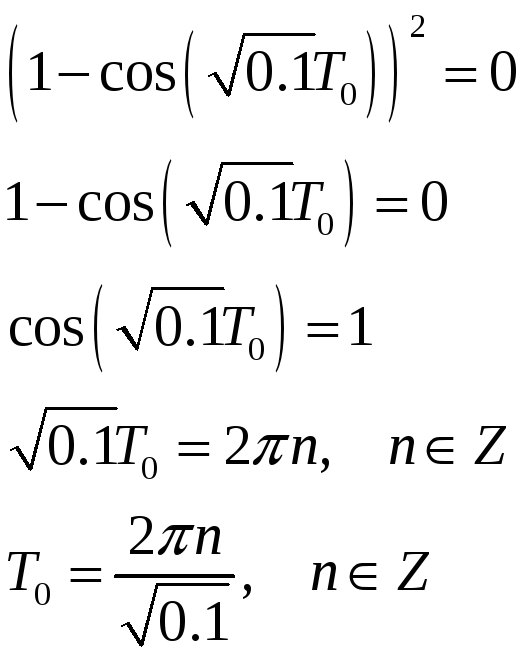
Таким образом, при любом положительном значении периода дискредитации замкнутая импульсная система будет неустойчивой. При замкнутая импульсная система будет находиться на границе устойчивости.

Получим график выходной величины замкнутой импульсной системы, находящейся на границе устойчивости.

С помощью пакета MatLab рассчитаем значение периода дискредитации , при котором замкнутая импульсная система будет находиться на границе устойчивости.

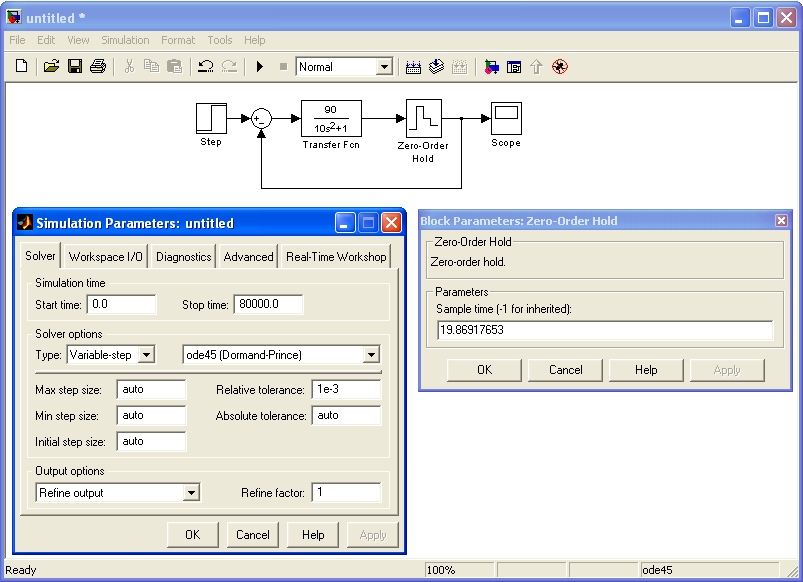
Выходная величина замкнутой импульсной системы при =19.86917653 представляет собой незатухающие гармонические колебания с постоянной амплитудой. Таким образом, замкнутая импульсная система находится на границе устойчивости.

Так как исследуемая система является неустойчивой при любых положительных значениях общего коэффициента передачи системы k и периода дискредитации , то говорить о качестве процесса регулирования не имеет смысла.

3. Вывод

В данной работе было проведено исследование импульсной системы автоматического управления. Исследовали влияние на характеристики импульсной системы изменения периода дискредитации и общего коэффициента передачи системы k. Были приобретены навыки в составлении структурных схем импульсных САУ с помощью пакета прикладных программ.