4. Сложение гармонических колебаний

Результат сложения гармонических колебаний зависит от направления складываемых колебаний, а так же от соотношения между их частотами, фазами и амплитудами. Рассмотрим на качественном уровне два случая.

4.1. Колебания, происходящие вдоль одной прямой с одинаковыми частотами

В этом случае складываемые колебания различаются лишь амплитудами А₁ иА₂ и начальными фазами₀₁ и ₀₂ . Сложение таких колебаний приведет к результату:

А₁ sin ( t + ₀₁ ) + А₂ sin( t + ₀₂ ) = А sin ( t + ₀ ) . (19)

Закон изменения смещения со временем в результирующем колебании - гармонический,частота результирующего колебания равна частоте складываемых колебаний.

Амплитуда результирующего колебания А зависит от амплитудА₁ иА₂, а также от разности начальных фаза₀₁ и ₀₂ . Несложные математические вычисления позволяют выразить амплитудуАследующим образом:

(20)

Начальная фаза ₀определяется из соотношения:

(21)

Таким образом, в рассматриваемом случае результат сложения колебаний определяется формулой (19), а входящие в неё амплитуда и начальная фаза - формулами (20) и (21).

4.2. Колебания происходят вдоль одной прямой с разными частотами

Представим два складываемых колебания графически (см.рис 4)

При сложении гармонических колебаний, происходящих с разными частотами₁и₂ ( периодамиТ₁ и Т₂) результирующее колебание не будет гармоническим, а будет представлятьсложное периодическое движение. Если складываются гармонические колебания с кратными частотами (например, на рис.4 ₂= 4₁), топериод результирующего колебания Т совпадает с периодом Т₁ слагаемогонаименьшей частоты:Т = Т₁ или =₁ .

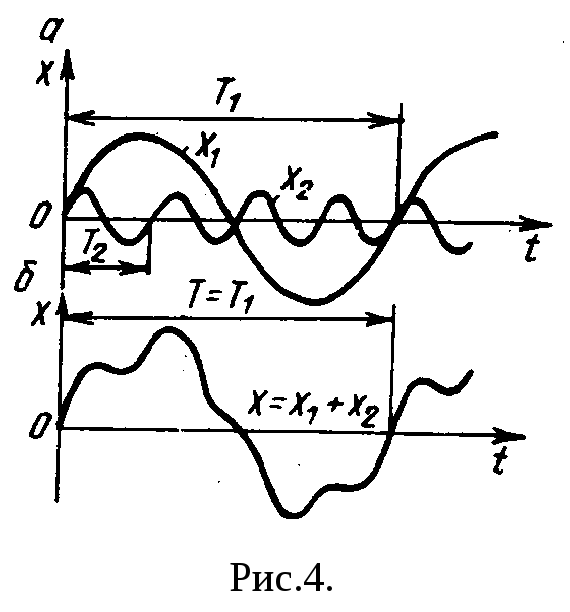
5. Разложение колебаний в ряд Фурье. Гармонический спектр сложных колебаний

Рассмотрение рис.4 приводит к утверждению, обратному сказанному выше и известному как теорема Фурье: любое сложное периодическое движение x(t) = x(t +T) c периодом Т можно представить в виде суммы простых составляющих гармонических колебаний (гармоник). Частоты этих гармоник кратны основной частоте  рассматриваемого периодического процесса.

Первая гармоника имеет частоту  = 2 /Т , вторая -2, третья -3и т.д.

Это утверждение можно записать в виде формулы, представляющей ряд Фурье:

(22)

Здесь А_к - амплитуды складываемых гармоник, а_к - их начальные фазы. Первая гармоника, имеющая частоту , обладает амплитудойА₁, и начальной фазой₁ , вторая (с частотой2 ) имеет амплитуду А₂ и начальную фазу₂и т.д.

СлагаемоеА₀в формуле (22) представляет собой постоянную величину, имеющую смысл постоянной составляющей сложного периодического процесса. На рис.5 представлена периодическая функция х(t), описывающая процессы, где колебания некоторой величины (например, пульсовые изменения кровенаполнения сосуда) происходят на фоне ее среднего постоянного значения (например, среднего уровня кровенаполнения), которое и характеризуется величинойА₀ в формуле (22) .

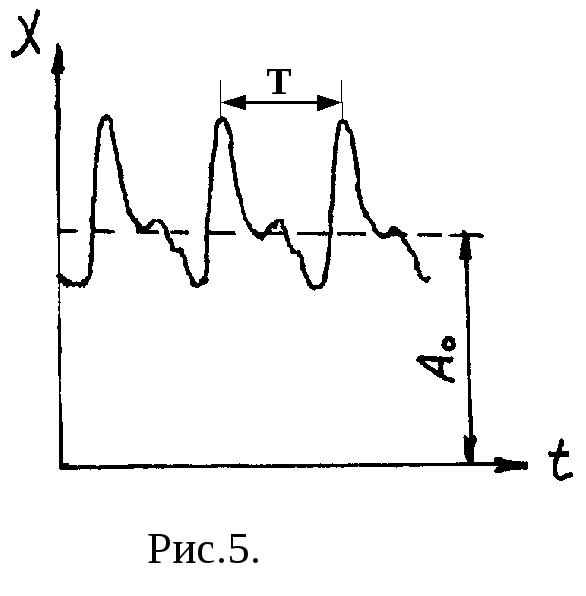
В записанной для общего случая формуле (22) число гармоник, входящих в состав сложного колебания , представляется бесконечно большим. При рассмотрении реальных колебательных процессов следует учесть, что вклад отдельных гармонических составляющих в анализируемое сложное колебание различен - в формулу (22) отдельные гармоники входят с разными амплитудами.

График, на котором по оси абсцисс отложены частоты гармоник, а по оси ординат - соответствующие им амплитуды, представляет собой гармонический спектр сложного колебания (см. рис.6).

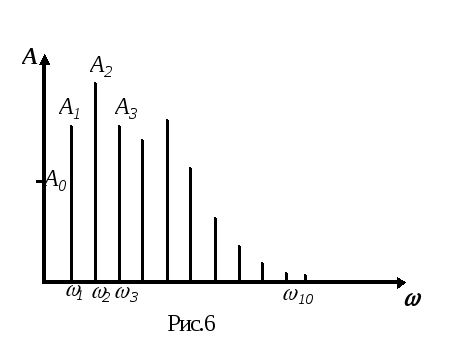
Из рассмотрения рис. 6 можно сделать вывод, что гармоники, частота которых превышает ₁₀, имеют малую амплитуды и, следовательно, их вклад в колебание, гармонический спектр которого представлен на рисунке, незначителен. Поэтому ряд Фурье для этого случая можно считать состоит из 10 слагаемых ( к= 1,2,3,.....,10 ), а вся информация о сложном колебательном процессе заключена в полосе частот от₁ (основная частота процесса) до₁₀.