12.7. Комбинации геометрических тел Сфера, вписанная в многогранник или тело вращения

Сфера называется вписанной в многогранник, если она касается всех граней многогранника.

Многогранник соответственно называется описанным около сферы.

Теоремы:

1. Сферу можно вписать в призму, если призма прямая и ее высота равна диаметру окружности, вписанной в основание призмы.

2. Сферу можно вписать в пирамиду, если в основание можно вписать окружность, а вершина пирамиды ортогонально проектируется в центр этой окружности.

3. Сферу можно вписать в любую правильную пирамиду.

Сфера называется вписанной в цилиндр, если она касается оснований и боковой поверхности цилиндра. Цилиндр соответственно называется описанным около сферы.

Теорема. Для того чтобы сферу можно было вписать в цилиндр, необходимо и достаточно, чтобы высота цилиндра равнялась диаметру его основания.

Сфера называется вписанной в конус, если она касается основания и боковой поверхности конуса. Конус соответственно называется описанным около сферы.

Теорема. Сферу можно вписать в любой конус.

Сфера называется вписанной в усеченный конус, если она касается оснований и боковой поверхности конуса. Усеченный конус соответственно называется описанным около сферы.

Теорема. Для того чтобы сферу можно было вписать в усеченный конус, необходимо и достаточно, чтобы образующая усеченного конуса равнялась сумме радиусов оснований.

Теорема. Сферу можно вписать в тело вращения, если в осевое сечение можно вписать окружность.

Сфера, описанная около многогранника

или тела вращения

Сфера называется описанной около многогранника, если все вершины многогранника лежат на сфере. Многогранник соответственно называется вписанным в сферу.

Теоремы:

1. Для того чтобы сферу можно было описать около призмы, необходимо и достаточно, чтобы призма была прямая и около основания можно было описать окружность.

2. Для того чтобы сферу можно было описать около пирамиды, необходимо и достаточно, чтобы около основания можно было описать окружность.

3. Сферу можно описать около любой правильной пирамиды.

Сфера называется описанной около цилиндра, если окружности оснований цилиндра лежат на сфере. Цилиндр соответственно называется вписанным в сферу.

Теорема. Сферу можно описать около любого цилиндра.

Сфера называется описанной около конуса, если окружность основания и вершина конуса лежат на сфере. Конус соответственно называется вписанным в сферу.

Теорема. Сферу можно описать около любого конуса.

Сфера называется описанной около усеченного конуса, если окружности оснований конуса лежат на сфере. Усеченный конус соответственно называется вписанным в сферу.

Теорема. Сферу можно описать около любого усеченного конуса.

Многогранники и тела вращения

Цилиндр называется описанным около призмы, если окружности оснований цилиндра описаны около оснований призмы, а боковые ребра призмы являются образующими цилиндра. Призма соответственно называется вписанной в цилиндр.

Теорема. Для того чтобы около призмы можно было описать цилиндр, необходимо и достаточно, чтобы призма была прямая и около ее основания можно было описать окружность.

Цилиндр называется вписанным в призму, если окружности его оснований вписаны в основания призмы, а боковая поверхность касается боковых граней призмы.

Теорема. Для того чтобы в призму можно было вписать цилиндр, необходимо и достаточно, чтобы призма была прямая и в ее основание можно было вписать окружность.

Конус называется описанным около пирамиды, если окружность основания конуса описана около основания пирамиды, а боковые ребра пирамиды являются образующими конуса. Пирамида соответственно называется вписанной в конус.

Теорема. Для того чтобы около пирамиды можно было описать конус, необходимо и достаточно, чтобы боковые ребра пирамиды были равны.

Конус называется вписанным в пирамиду, если окружность его основания вписана в основание пирамиды, а боковая поверхность касается боковых граней пирамиды. Пирамида соответственно называется описанной около конуса.

Теорема. Для того чтобы в пирамиду можно было вписать конус, необходимо и достаточно, чтобы в основание пирамиды можно было вписать окружность, а вершина пирамиды ортогонально проектировалась в центр этой окружности.

Пример 1. Шар вписан в прямую призму, основанием которой является прямоугольный треугольник с катетом a и противолежащим ему острым углом α. Найти объем призмы.

Решение. Сделаем рисунок (рис. 12.48). Шар вписан в прямую призму, значит, высота призмы равна диаметру шара, а в треугольник основания вписана окружность, радиус которой равен радиусу шара. Рассмотрим прямоугольный треугольник ABC, у которого катет BC = a, противолежащий ему BAC = α. Найдем катет AC и гипотенузу AB:

Рис. 12.48

Площадь треугольника ABC равна:

Вычислим радиус окружности, вписанной в треугольник:

Вычисляем объем призмы по формуле

Получаем ответ:

Пример 2. Боковое ребро правильной четырехугольной пирамиды равно a. Двугранный угол, образованный смежными боковыми гранями, равен β. Найти радиус шара, описанного около этой пирамиды.

Решение. Сделаем рисунок (рис. 12.49): ABCD – квадрат, SO – высота пирамиды, AEC =  – двугранный угол.

Рассмотрим диагональное сечение пирамиды – треугольник SBD (SB = SD). Радиусом шара, описанного около данной пирамиды, будет радиус окружности, описанной около треугольника SBD. Найдем его по формуле

Рис. 12.49

Из подобия треугольников (SOB = SEO = 90, BSO = OSE) следует пропорциональность сторон: SB/SO = BO/OE.

Из треугольника найдемТак какАО = ВО, то Следовательно,

Вычисляем радиус окружности:

Получаем ответ:

Пример 3. В усеченный конус вписан шар радиуса R. Образующая конуса наклонена к плоскости основания под углом . Найти объем усеченного конуса.

Решение.Рассмотрим осевое сечение конуса (рис. 12.50).

Рис. 12.50

Введем обозначения: R₁ – радиус нижнего основания конуса, R₂ – радиус верхнего основания. Высота данного усеченного конуса будет равна диаметру вписанного в него шара 2R. Рассмотрим прямоугольный треугольник ABC: B = 90, A = , BC = 2R. Найдем катет BA и гипотенузу AC: BA = BC  ctg, Так как в усеченный конус вписан шар, то образующая этого конуса равна сумме радиусов его оснований. Получим равенство:

Заметим, что

Решив систему найдем

Вычисляем объем усеченного конуса по формуле (12.8).

Получаем ответ:

Пример 4. В шар радиуса R вписан конус, образующая которого составляет с плоскостью основания угол φ. Найти площадь полной поверхности конуса.

Решение. Для вычисления площади полной поверхности конуса необходимо знать радиус основания и образующую конуса. Рассмотрим осевое сечение данного конуса – равнобедренный треугольник SAB: SA = SB – образующие, SD – высота, DB – радиус основания конуса (рис. 12.51).

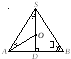
Рис. 12.51

По условию задачи SAD = φ, следовательно, ТреугольникAOS – равнобедренный (AO = OS = R), поэтому Внешний угол этого треугольника при вершине О равен: AOD = SAO + ASO =  – 2.

Из треугольника AOD (D = 90, AO = R, AOD =  – 2) выразим AD:

Из треугольника ASD (D = 90, AD = Rsin 2) выразим SA:

Подставив найденные выражения в формулу для вычисления площади полной поверхности конуса, получим:

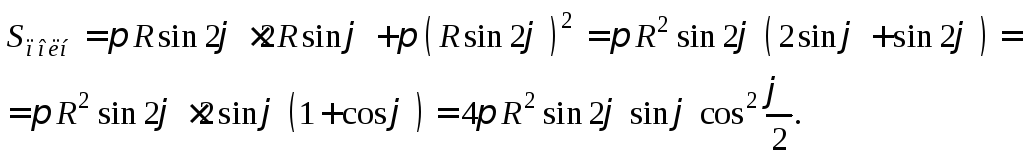
Таким образом,

Пример 5. В прямой параллелепипед вписан цилиндр, объем которого в m раз меньше объема параллелепипеда. Найти двугранные углы при боковых ребрах параллелепипеда.

Решение.Двугранными углами при боковых ребрах данного параллелепипеда являются углы параллелограмма, лежащего в его основании. В параллелепипед вписан цилиндр, значит, в параллелограмм основания вписана окружность. Если в четырехугольник вписана окружность, то суммы длин противолежащих сторон четырехугольника равны. Таким образом, основанием параллелепипеда является ромб. Сделаем рисунок (рис. 12.52).

Рис. 12.52

Обозначим искомый угол . Из треугольника ABC (C = 90, A = ) найдем сторону ромба AB и его высоту BC:

Так как высоты цилиндра и параллелепипеда равны, то площадь основания цилиндра будет в m раз меньше площади основания параллелепипеда. Запишем равенство: и выразим из негодалее

Двугранные углы при боковых ребрах параллелепипеда будут равны:

и

Задания