4. Деление десятичных чисел в эвм

Деление представляет многошаговый процесс. Для определения цифр частного необходимо произвести последовательное вычитание делителя из делимого, при этом если очередной остаток положительный или равен нулю, то в соответствующий разряд частного добавляется единица. Деление можно производить с восстановлением и без восстановления остатка.

При делении без восстановления остатка в том случае, когда образуется отрицательный остаток, делитель сдвигают на один десятичный разряд вправо по отношению к остатку и продолжают деление, прибавляя делитель к отрицательному остатку с приписанным справа следующим разрядом делимого. После первого такого прибавления в очередном разряде частного устанавливается цифра 9. На каждом очередном этапе сложения содержимое этого разряда частного уменьшается на единицу. При новом появлении положительного остатка в данном разряде зафиксируется искомая цифра разряда частного. Далее осуществляется переход к определению следующей цифры частного.

Если делимое не делится нацело, то для целей округления можно определить дополнительную цифру частного.

Пример.

Вычислить десятичное частное 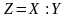при 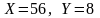по методу с восстановлением остатка.

Для простоты и наглядности операции будем производить вначале деление в десятичной системе счисления.

Сумматор Частное

Делимое 0 5 6

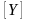_доп. = 920 + 9 2 0

Восстановление 9 7 0 0 (остаток меньше 0)

остатка _пр. = 080 + 0 8 0

1

0 5 6

Сдвиг делителя 9 9 2

_доп. = 992 0 4 8 01 (остаток больше 0)

+ 9 9 2

0 4 0 02 (остаток больше 0)

+ 9 9 2

0 3 2 03 (остаток больше 0)

+ 9 9 2

0 2 4 04 (остаток больше 0)

+ 9 9 2

0 1 6 05 (остаток больше 0)

+ 9 9 2

0 0 8 06 (остаток больше 0)

+ 9 9 2

0 0 0 07 (остаток равен 0)

Таким образом, Z=X : Y= 7.

Пример.

Теперь рассмотренный пример деления с восстановлением остатка представим в -кодах.

Делимое X=65, делитель Y=8, Z = X : Y.

Ниже приводится схема реализации деления в D-кодах.

Сумматор Частное

Делимое [056] 0000 0101 0110

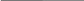[080] 1111 1000 0000

1111 1101 0110

коррекция 1010 1010 0000

(976) 1001 0111 0110 < 0 0

Восстановление [080] 0110 1110 0110

0000 0101 1100

коррекция 0000 0000 1010

1

(056) 0000 0101 0110

[008] 1111 1111 1000

0000 0100 1110

коррекция 0000 0000 1010

(048) 0000 0100 1000 > 0 01

[008] 1111 1111 1000

0000 0100 0000

коррекция 0000 0000 0000

(040) 0000 0100 0000 > 0 02

[008] 1111 1111 1000

0000 0011 1000

коррекция 0000 0000 1010

(032) 0000 0011 0010 > 0 03

[008] 1111 1111 1000

0000 0010 1010

коррекция 0000 0000 1010

(024) 0000 0010 0100 > 0 04

[008] 1111 1111 1000

0000 0001 1100

коррекция 0000 0000 1010

(016) 0000 0001 0110 > 0 05

[008] 1111 1111 1000

0000 0000 1110

коррекция 0000 0000 1010

(008) 0000 0000 1000 > 0 06

[008] 1111 1111 1000

0000 0000 0000 = 0 07

Таким образом, Z = X : Y = 7.

В заключение рассмотрим пример деления десятичных чисел без восстановления остатка.

Пример.

Вычислить десятичное частное Z = X :Y при X=56, Y=8 по методу без восстановления остатка в десятичной системе счисления.

Сумматор Частное

+

Делимое 0 5 6

_доп. = 920 9 2 0

+

1

9 7 6 0 (остаток меньше 0)

Сдвиг делителя 0 0 8

+

_пр. = 008 9 8 4 09 (остаток меньше 0)

0 0 8

+

9 9 2 08 (остаток меньше 0)

0 0 8

0 0 0 07 (остаток равен 0)

Таким образом, Z=X : Y= 7.

Вышеприведенный пример деления без восстановления остатка рассмотрим теперь в -кодах. Делимое X=56, делитель Y=8, Z = X : Y.

Сумматор Частное

Делимое [056] 0000 0101 0110

[080] 1111 1000 0000

1111 1101 0110

коррекция 1010 1010 0000

1

(976) 1001 0111 0110 < 0 0

[008] 0110 0110 1110

1111 1110 0100

коррекция 1010 0000 1010

(984) 1001 1000 0100 < 0 09

[008] 0110 0110 1110

1111 1111 0010

коррекция 1010 1010 0000

(992) 1001 1001 0010 < 0 08

[008] 0110 0110 1110

0000 0000 0000 = 0 07

Следовательно, Z=X : Y = 7.

4. АЛГОРИТМИЧЕСКИЕ МОДЕЛИ ВЫПОЛНЕНИЯ

АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ

4.1. Проектирование универсального алгоритма перевода чисел

в разные системы счисления

Перевод чисел из одной позиционной системы счисления в другую выполняется по разным алгоритмам для целых и дробных частей числа [12].

Алгоритм 1. Для перевода целого числа из системы счисления с основанием p в систему счисления с основанием q нужно делить число и его частные на q. Последовательное деление производится до тех пор, пока не получится частное, равное нулю. Деление выполняется в исходной системе счисления. При этом в виде остатков от деления получаются q-ичные цифры (начиная с младшей) числа.

Алгоритм 2. Для перевода правильной дроби (дробной части числа) из p-ичной в q-ичную систему счисления нужно умножать эту дробь и дробные части полученных произведений на q. Целые части этих произведений образуют q-ичные цифры (начиная со старшей) представления правильной дроби в q-ичной системе счисления. Умножение выполняется в исходной системе счисления.

Алгоритм 3. Если результирующей системой счисления (p) - десятичная, то наиболее простой способ перевода - это перевод по весовым коэффициентам:

X_q = x_n-1*q^n-1 + x_n-2*q^n-2 + … + x₁*q¹ + x₀*q⁰ + x_-1*q^-1 + x_-2*q^m-2 + … + x_k*q^k

или при алгоритмической реализации нужно вычислить сумму следующего вида:

_n-1

X_q =  x_i*qⁱ ,

^i=-t

где n – количество разрядов в целой части числа, t – количество разрядов в дробной части числа.

Алгоритм 4. Частным случаем перевода чисел из одной системы счисления в другую служит ситуация, когда основание одной системы счисления является целой степенью другой (p=q^k). В этом случае для перевода произвольного числа из q-ичной системы счисления в p-ичную нужно цифры числа влево и вправо от запятой разбить на группы по k разрядов в каждой. При этом если необходимо, крайнюю левую и крайнюю правую группы дополняют нулями до k цифр в группе. Затем надо заменить каждую выделенную k-значную группу цифрой в p-ичной системе счисления.

Р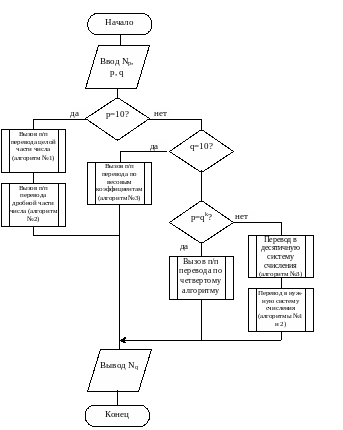 ис. 4.1. Схема универсального алгоритма перевода чисел

из одной системы счисления в другую

Схема универсального алгоритма перевода чисел из любой системы счисления в любую представлена на рис. 4.1, где частные алгоритмы оформлены подпрограммами. Число X в исходной системе счисления с основанием p в ней переводится в q-ичную систему счисления. Если p=10, то число разделяют на целую и дробную части, для перевода которых применяют алгоритмы 1 и 2 соответственно. Если результирующая система счисления является десятичной, то используют третий алгоритм. Если ни исходная, ни результирующая системы не являются десятичными, но p=q^k, то пользуются четвертым алгоритмом. В случае, когда не выполняется ни одно из перечисленных условий, приходится сначала переводить число в десятичную систему счисления, после чего – в искомую. Это обусловлено сложностью выполнения операций в непривычных для человека системах счисления.