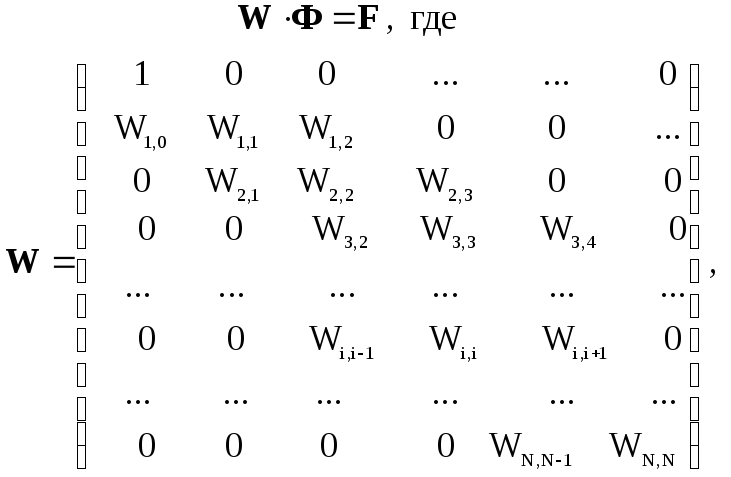- •1. Математические модели технической физики
- •2. Физико-математическая классификация дифференциальных уравнений в частных производных
- •3. Дискретизация функций одной переменной
- •4. Дискретизация дифференциальных уравнений в частных производных
- •4.1 Метод конечных разностей
- •4.2 Метод конечных элементов
- •4.3 Метод конечных объемов
- •5. Свойства дискретных схем
- •5.1 Точность
- •5.2 Согласованность
- •5.3 Устойчивость
- •5.4 Сходимость
4.2 Метод конечных элементов
В
основе метода
конечных элементов
(МКЭ) лежит предположение о характере
поведения функции
![]() ,
являющейся точным решением дифференциального
уравнения. Для демонстрации основных
идей МКЭ, предположим, что с достаточной
точностью искомое решение
,
являющейся точным решением дифференциального
уравнения. Для демонстрации основных
идей МКЭ, предположим, что с достаточной
точностью искомое решение![]() (x)
может быть представлено с помощью
кусочно-линейной интерполяции26
(рис. 9).
(x)
может быть представлено с помощью
кусочно-линейной интерполяции26
(рис. 9).
Очевидно, что значение кусочно-линейной функции Ф*=Ф(х*) в некоторой точке х*, лежащей внутри отрезка [xi-1, xi] может быть найдено по формуле:

Рис. 9. Кусочно-линейная интерполяция решения дифференциального уравнения
|
|
(27) |
где
|
|
(27а) |
График
функции формы
(пробной
функции)
![]() ,
приведен на рис. 10. Необходимо отметить,
что функция формы, являетсялокальной,
т.е. она отлична от нуля лишь в некоторой
области, непосредственно прилегающей
к рассматриваемому узлу xi.
В частности, в случае кусочно-линейной
интерполяции функции одной переменной
,
приведен на рис. 10. Необходимо отметить,
что функция формы, являетсялокальной,
т.е. она отлична от нуля лишь в некоторой
области, непосредственно прилегающей
к рассматриваемому узлу xi.
В частности, в случае кусочно-линейной
интерполяции функции одной переменной
![]() (x),
функция формы
(x),
функция формы![]() отлична от нуля лишь в пределах отрезков
(конечных
элементов)
[xi-1,
xi]
и [xi,
xi+1].
отлична от нуля лишь в пределах отрезков
(конечных
элементов)
[xi-1,
xi]
и [xi,
xi+1].

Рис.
10. Линейная функция формы
![]()
Отметим также, что производная кусочно-линейной функции Ф(х) в пределах элемента [xi-1, xi] совпадает с конечно-разностным отношением назад (9а), а в пределах элемента [xi, xi+1] – с конечно-разностным отношением вперед (9b).
Продемонстрируем
применение метода конечных элементов
на примере рассмотренного нами ранее
обыкновенного дифференциального
уравнения (13). Для сокращения записи
будем использовать обозначение F(x)=
![]() .
.
Подстановка
в уравнение (13) вместо точного решения
![]() (x)
кусочно-линейной функции Ф(х) приведет
к тому, что уравнение (13) будет выполняться
неточно. Можно записать:
(x)
кусочно-линейной функции Ф(х) приведет
к тому, что уравнение (13) будет выполняться
неточно. Можно записать:
|
|
(28) |
Или:
|
|
(28а) |
где
R(х)
– невязка
решения, в общем случае являющаяся
функцией независимой переменной х.
Очевидно, что кусочно-линейная функция
Ф(х) будет хорошим приближением к точному
решению
![]() (x)
лишь в том случае, если невязкаR(x)
будет мала для всех значений х[
х0;
хN].
(x)
лишь в том случае, если невязкаR(x)
будет мала для всех значений х[
х0;
хN].
Второй
принципиальный этап МКЭ заключается в
выборе способа определения неизвестных
узловых значений Фi.
Для решения этой задачи потребуем, чтобы
взвешенные
интегралы невязки
по всей области задания функции
![]() (x)
были равны нулю:
(x)
были равны нулю:
|
|
(29) |
Вследствие
локальности функций формы
![]() (см. рис. 10), можно записать:
(см. рис. 10), можно записать:
|
|
(30) |
Или:
|
|
(30а) |
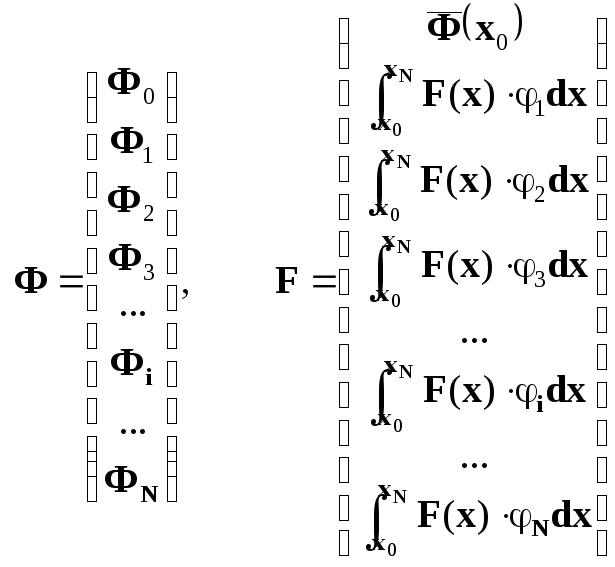
Все
интегралы, входящие в (30а), могут быть
сравнительно легко определены, а сами
соотношения (30а), совместно с начальным
условием Ф0=![]() (х0),
являются системой линейных алгебраических
уравнений, которая может быть решена
любым из известных методов, т.е.:
(х0),
являются системой линейных алгебраических
уравнений, которая может быть решена
любым из известных методов, т.е.:
|
|
(30b) |
Следует обратить внимание на то, что матрица системы линейных алгебраических уравнений (30b) имеет специфическую диагональную (ленточную) структуру. Для решения систем уравнений с ленточными матрицами, в вычислительной математике разработан ряд специальных методов, позволяющих существенно уменьшить объем вычислительной работы, самый распространенный из этих методов, называется методом прогонки.
Результаты решения дифференциального уравнения (13) методом конечных элементов приведены на рис. 11. Как можно видеть из этого рисунка, уже при шаге сетки Δх=0,08 численное решение, полученное с помощью МКЭ, гораздо лучше соответствует точному решению, чем численное решение, полученное с помощью метода Эйлера при шаге сетки Δх=0,025 (см. рис. 4). Следует, однако, отметить, что объем вычислительной работы, связанный с определением интегралов, входящих в (30), и последующее решение полученной системы алгебраических уравнений, на порядок превосходит объем вычислительной работы, выполненной по методу Эйлера.
Метод
конечных элементов естественным образом
распространяется на случай функций
нескольких переменных. При этом, как
правило, оказывается удобнее задавать
каждую из функций формы в локальной
системе координат,
связанной с рассматриваемым узлом
расчетной сетки. В качестве примера, на
рис. 12 приведен график полилинейной
функции формы
![]() ,
определенной на плоской сетке, содержащей
треугольные конечные элементы.
,
определенной на плоской сетке, содержащей
треугольные конечные элементы.
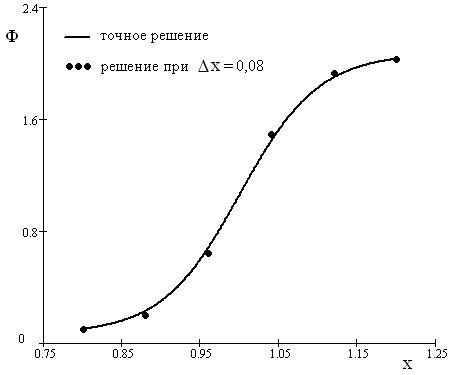
Рис. 11. Решение дифференциального уравнения (13) методом конечных элементов

Рис.
12. Полилинейная функция формы
![]() ,
определенная на плоской сетке,
,
определенная на плоской сетке,
содержащей треугольные конечные элементы

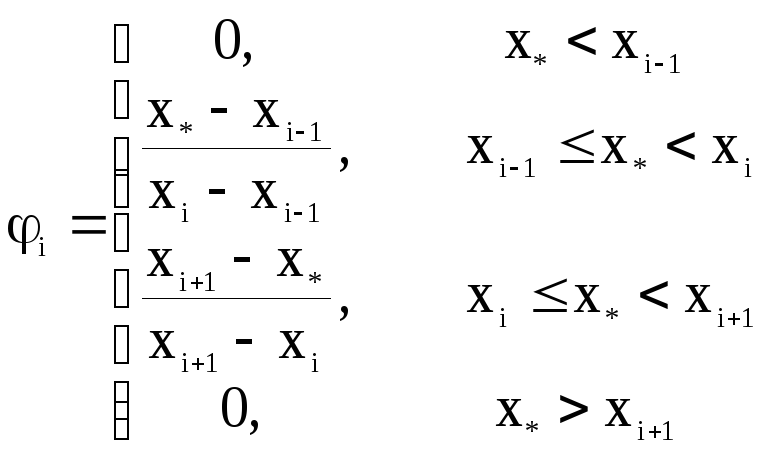 .
.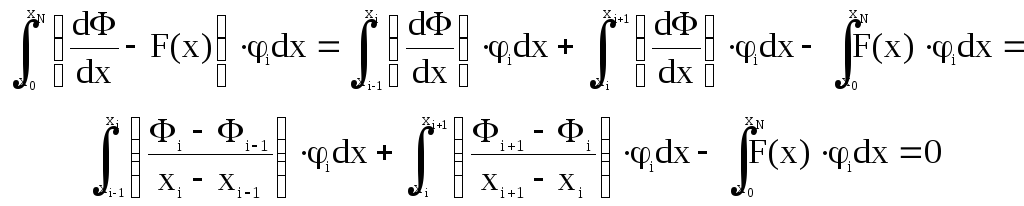 для
всех i=1…N
для
всех i=1…N