
- •Глава 14. Неопределенный интеграл, структура интегрирования. Таблица неопределённых интегралов и правила интегрирования.
- •§14.1. Неопределенный интеграл
- •14.1.1. Основные определения
- •14.1.2.Таблица основных интегралов
- •14.1.3.Правила интегрирования
- •§14.2. Интегрирование рациональных функций
- •14.2.1.Алгебраическое введение
- •14.2.2. Неопределенный интеграл от рациональной функции
- •§14.3. Интегрирование иррациональных функций
- •14.3.1.Интегрирование выражений
- •14.3.2.Интегрирование выражений вида . Подстановки Эйлера
- •§14.4. Интегрирование тригонометрических функций
- •14.4.1. Интегралы вида
- •Интегрирование биномиальных дифференциалов.
Интегрирование биномиальных дифференциалов.
Примеры. Биномиальным называется дифференциал вида.
![]() ,
,
где a, b – любые показатели m, n, p – рациональные числа. Выясним случаи, когда эти выражения интегрируются в конечном виде.
Один такой случай
ясен непосредственно: если p – число
целое (положительное, нуль или
отрицательное), то рассматриваемое
выражение относится к типу, изученному
в предыдущем
![]() .
Именно, если через
.
Именно, если через
![]() обозначить наименьшее общее кратное
знаменателей дробей
обозначить наименьшее общее кратное
знаменателей дробей
![]() и
и
![]() ,
то мы имеем здесь выражение вида
,
то мы имеем здесь выражение вида
![]() ,
так что для рационализации его достаточна
подстановка
,
так что для рационализации его достаточна
подстановка
![]() .
.
Преобразуем теперь
данное выражение подстановкой
![]() .
.
Тогда
![]()
![]()
и, положив для краткости
![]() ,
,
будем иметь
![]() .
.
Если
![]() -
число целое, то мы снова приходим к
выражению изученного типа. Действительно,
если обозначить через
-
число целое, то мы снова приходим к
выражению изученного типа. Действительно,
если обозначить через
![]() знаменатель дроби
знаменатель дроби
![]() ,
то преобразованное выражение имеет вид
,
то преобразованное выражение имеет вид
![]() . Рационализации подынтегрального
выражения можно достигнуть и сразу –
подстановкой
. Рационализации подынтегрального
выражения можно достигнуть и сразу –
подстановкой
![]() .
.
Наконец, перепишем второй из интегралов (2) так:
![]() .
.
Легко усмотреть,
что при
![]() целом мы также имеем изученный случай:
преобразованное выражение имеет вид
целом мы также имеем изученный случай:
преобразованное выражение имеет вид
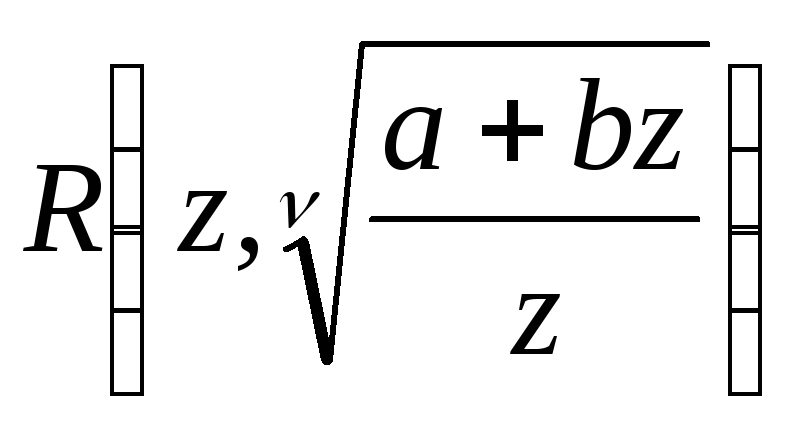 .
Подынтегральное выражение в данном
интеграле рационализируется и сразу
подстановкой
.
Подынтегральное выражение в данном
интеграле рационализируется и сразу
подстановкой
![]()
Таким образом, оба интеграла (2) выражаются в конечном виде, если оказывается целым одно из чисел
![]() или
(что то же) одно из чисел
или
(что то же) одно из чисел
![]() .
.
Эти случаи интегрируемости, по существу, известны были ещё Ньютону. Однако лишь в середине девятнадцатого столетия П.Л. Чебышев установил замечательный факт, что других случаев интегрируемости в конечном виде для биноминальных дифференциалов нет.
Рассмотрим примеры.
1)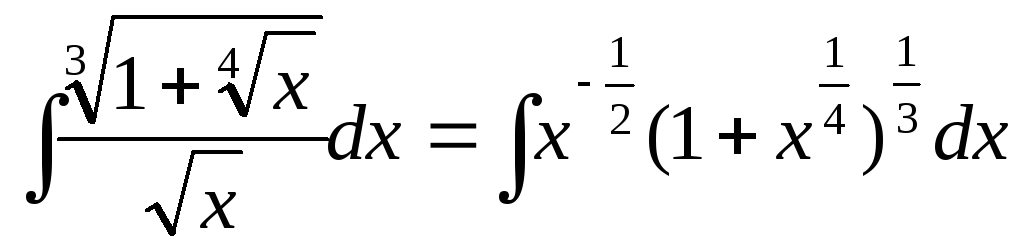 .
Здесь
.
Здесь
![]() ,
,
![]() ,
,![]() ;
так как
;
так как
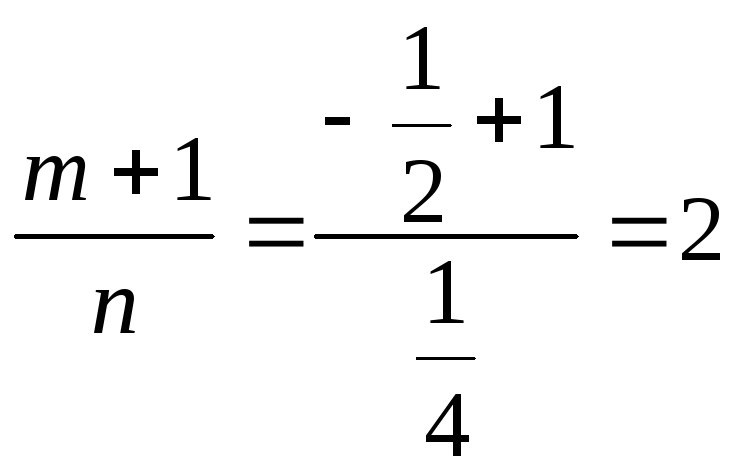 ,
,
то имеем второй
случай интегрируемости. Заметив, что
![]() ,
положим (по общему правилу)
,
положим (по общему правилу)
![]() ,
,
![]() ,
,
![]() ;
;
тогда
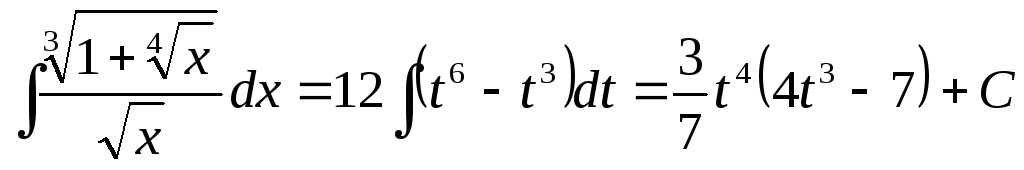 и т.д.
и т.д.
2)
![]() .
.
