chirskii-lectures-4sem

x(u,v + ∆v)− x(u,v)= ∂∂xv (u,v)∆v + o(∆v) y(u,v + ∆v)− y(u,v)= ∂∂yv (u,v)∆v + o(∆v) x(u + ∆u,v)− x(u,v)= ∂∂ux (u,v)∆u +o(∆u) y(u + ∆u,v)− y(u,v)= ∂∂uy (u,v)∆u + o(∆u)

x(u + ∆u,v + ∆v)− x(u,v + ∆v)= ∂∂ux (u,v + ∆v)∆u + o(∆u) y(u + ∆u,v + ∆v)− y(u,v + ∆v)= ∂∂uy (u,v + ∆v)∆u + o(∆u) x(u + ∆u,v + ∆v)− x(u + ∆u,v)= ∂∂xv (u,v + ∆v)∆v +o(∆v) y(u + ∆u,v + ∆v)− y(u + ∆u,v)= ∂∂yv (u,v + ∆v)∆v + o(∆v)

При малых ∆u, ∆v производные

∂x

,

∂x ,

∂y ,

∂y , вычисленные в точках

∂u

∂v

∂u

∂v

(u + ∆u,v),(u,v + ∆v),

мало

отличаются от

соответствующих

производных,

вычисленных в точке (u,v),

−

−

мало

отличаются

от

поэтому r u (u,v), r v (u,v)

−

−

и

−

−

соответственно,

и

r u (u + ∆u,v), r v (u + ∆u,v)

r u (u,v + ∆v), r v (u,v + ∆v),

рассматриваемый

четырёхугольник

представляет

собой

«почти

параллелограмм».

Площадь параллелограмма со сторонами

u ,

v

r

r

u

r

r

v

∂x

∂x

равна модулю определителя

∂u

∂v = J

, т.е. равна

J

.

∂y

∂y

∂u ∂v

11

Поэтому

при

преобразовании

интегральная

сумма

n

∑ f (x(ui ,vi ), y(ui ,vi

))

J (ui ,vi

)

∆u∆v

близка

к

интегральной

сумме

i=1

n

)пл.(Di

),

∑ f (xi , yi

и т.к.

соответствующие

интегральные суммы для

i=1

интегралов, стоящих в правой и левой частях доказываемого равенства мало отличаются друг от друга, то и интегралы совпадают.

Замечание. Утверждение теоремы сохранится, если условие взаимной

однозначности отображения x = x(u, v), y = y(u, v)				нарушится на	множестве
нулевой площади.
Пример. Переход к полярным координатам.
Пусть	требуется	вычислить	∫∫ f (x, y)dxdy	по области	D, которая
			D
задаётся	в	полярных	координатах		условиями
α ≤φ ≤ β

r ≤ r(φ)

Сделаем замену переменных

x = r cosφ

y = r sinφ

При этой замене нарушается взаимная однозначность отображения. Точке (0,0) соответствует целый отрезок [α, β] на оси φ . Однако точка и

отрезок имеют нулевую площадь, и теорема справедлива. Осталось

вычислить

J.

∂x

= cosφ,

∂y

= sinφ,

∂x

= −r sinφ,

∂y

= r cosφ.

∂r

∂r

∂φ

∂φ

J =

cosφ

−r sinφ

= r cos2

φ + r sin 2 φ = r

sinφ

r cosφ

Следовательно, ∫∫ f (x, y)dxdy = ∫αβ dφ∫0r (φ ) f (r cosφ, r sinφ)rdr .

D

Полярные координаты бывают очень полезны при вычислениях.

Рассмотрим пример. Найти I = ∫0∞ e−x2 dx .

12

Решение. I — это несобственный интеграл, и прежде всего			следует
установить его сходимость. По определению,	∞∫e−x2 dx = ∫1 e−x2 dx +		∞∫e−x2 dx .
	0	0	1

Первый из интегралов — собственный, второй — сходится по 1-й теореме о

сравнении,

так

как

при

x ≥1

справедливы

неравенства

x2 ≥ x −x2

≤ −x,e−x2 ≤ e−x , а ∞∫e−x dx , очевидно, сходится.

1

Обозначим

IR

= R∫e−x2 dx

(очевидно,

IR → I,R →∞). Тогда, поскольку

0

обозначение

переменной интегрирования можно

выбрать

произвольным,

IR2 = IR IR = R∫e−x2 dx 0R∫e−y2 dy = ∫∫e−x2 −y2 dxdy , где SR

— квадрат, а CR ,C 2R —

0

SR

четверти круга, соответственно, радиусов R

и

2R . Так как e−x2 −y2 ≥ 0 , то по

свойствам 2

и

3 двойного

интеграла

∫∫e−x2 −y2 dxdy ≤ IR2

≤ ∫∫e−x2 −y2 dxdy . В

CR

C 2R

интеграле ∫∫e−x2 −y2 dxdy перейдем к полярным координатам:

CR

−x2 −y2

π/ 2

R

−r2

πR

−r2 1

2

π

−r2

R

π

(1 − e

−R 2

).

∫∫e

dxdy = ∫dφ∫e

rdr =

∫e

dr =

2

4

e

=

4

CR

0

0

2

0

0

Аналогично,

∫∫e−x2 −y2 dxdy =

π

(1 − e−2R 2 )и

π(1 − e−R 2 dx)≤ IR2 ≤ π

(1 − e−2R 2 dx). При

C 2R

4

4

4

стремлении R к ∞ получаем, что limIR2 =	π	, то есть I2	=	π	,I =	π .
R→∞	4			4		2

4. Тройные интегралы

Рассмотрим кубируемую область в трехмерном пространстве V R3 .

Разбиение T на части Vi осуществляется непрерывными поверхностями.

Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции f (x, y,z), разбиения T области V и

13

выбранных	точек	Mi (xi , yi ,zi ) Vi	интегральную	сумму
σ(f ,T ,{M i })= ∑n	f (M i )µ(Vi	), где µ(Vi ) обозначает объем области Vi .
i=1
Определение. Пусть I R такое число, что ε > 0 δ > 0				T,d(T)< δ

{µi }σ(f ,t{µi })− I <ε . Тогда мы говорим, что f интегрируема на V, число I

есть интеграл f по области V и обозначаем это так: I = ∫∫∫f (x, y,z)dxdydz .

V

Как и в случае двойного интеграла, выполняются аналогичные свойства 1-6. Можно доказать, что если f (x, y,z) непрерывна на V, то она интегрируема на V. Точно также можно убедиться в том, что если точки разрыва f лежат на конечном числе непрерывных поверхностей, и разбивающих V на кубируемые области, то f интегрируема на V.

Вычисление тройного интеграла производится по следующему правилу.

Теорема.		Пусть	V	задана		следующими			неравенствами:
ψ1 (x, y)≤ z ≤ ψ2 (x, y),(x, y) D . D — квадрируемая								замкнутая		область на
плоскости, ψ1 ,ψ2		— непрерывные функции на D. Тогда
			ψ	(x, y )
∫∫∫ f (x, y, z)dxdydz = ∫∫dxdy 2				∫ f (x, y, z)dz
V		D	ψ1 (x, y )
Замечание.		Если	область			D	задана		неравенствами
a ≤ x ≤ b,φ1 (x)≤ y ≤ φ2 (x), где φ1 ,φ2					— непрерывные функции на [a,b], то
		b	φ2 (x ) ψ2		(x, y )
∫∫∫ f (x, y, z)dxdydz = ∫dx ∫dy					∫ f (x, y, z)dz.
V		a	φ1 (x )	ψ1 (x, y )
Сформулируем общую теорему о замене переменных.
Теорема.	Пусть отображение x = x(u,v, w),						y = y(u,v, w),			z = z(u,v, w)
устанавливает	взаимно		однозначное			соответствие между				областями
∆,(u,v, w) ∆ и		V ,(x, y, z) V ,		причем		функции		x, y, z	—	непрерывно

14

		∂x	∂x	∂x
		∂u	∂v	∂w
	дифференцируемые и J =	∂y	∂y	∂y		≠ 0 ни в одной точке ∆. Пусть
		∂u	∂v	∂w
		∂z	∂z	∂z
		∂u	∂v	∂w

f (x, y, z) — непрерывная функция. Тогда

∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (x(u,,v, w), y(u,v, w), z(u,v, w)) J dudvdw

V

∆

Как и для двойного интеграла, теорема остается верной в случае

нарушения ее условий на множестве нулевого объема.

Пример 1. Переход к цилиндрическим координатам. Он

осуществляется с помощью функций: x = r cosφ, y = r sin φ,z = z .

При

этом

якобиан

равен

cosφ

−r sin φ

0

cosφ

−r sin φ

= r cos2 φ+ r sin2 φ= r .

J =

sin φ

r cosφ

0

=

0

0

1

sin φ

r cosφ

Пример 2. Переход к сферическим координатам осуществляется

функциями x = r cosφcosψ, y = rsin φcosψ,z = rsin ψ.

Якобиан

преобразования

равен

cosφcosψ

−r sinφcosψ

−r cosφsinψ

J =

sinφcosψ

r cosφcosψ

−r sinφsinψ

=

sinψ

0

r cosψ

(разложение

по

3-й

строке)

= r cosψ

cosφcosψ

−r sinφcosψ

+sinψ

−r sinφcosψ

−r cosφsinψ

=

sinφcosψ

r cosφcosψ

r cosφcosψ

−r sinφsinψ

(выделим общие множители у столбцов)

r2 cos3 ψ

cosφ

−sin φ

+ r2 sin2 ψcosψ

−sin φ

− cosφ

= r2 cos3 ψ + r2 sin2 ψcosψ =

sin φ

cosφ

cosφ

−sin φ

= r2 cosψ(cos2 ψ + sin2 ψ)= r2 cosψ.

15

Криволинейные интегралы

1. Криволинейные интегралы первого типа

Рассмотрим спрямляемую (т.е. имеющую длину) кривую AB на плоскости (A, B – точки плоскости). Для простоты, считаем, что эта кривая задана параметрически x = x(t), y = y(t),t [T0 ;T1 ], причем x(t), y(t) – непрерывно дифференцируемые на отрезке функции такие, что каждому значению параметра соответствует единственная точка кривой.

Тогда длина кривой выражается формулой l = T∫1					(x′(t))2	+(y′(t))2 dt .
				T0
Под	разбиением		T кривой AB будем понимать множество точек
A = A0 , A1 ,..., An = B ,			лежащих на этой кривой и занумерованных в
направлении от A к B. Пусть ∆li - длина кривой Ai−1 , Ai .
Диаметр d(T) определим как d(T )= max ∆li .
				i=1,...,n
Пусть функция			f (M )= f (x, y) определена на кривой AB. Выберем на
каждом	участке		Ai−1 Ai	кривой точку M i	и	образуем сумму
σ(f ,T ,{M i })= ∑n		f (M i )∆li		, называемую интегральной.
	i−1
Определение.		Пусть		I R . Если ε > 0 δ > 0 T : d(T )<δ {M i }

σ(f ,T,{M i })− I < ε , то величина I называется криволинейным интегралом

первого типа по кривой AB и обозначается так: I = ∫ f (x, y)dl .

AB

Важное замечание. Если бы мы совершали движение по кривой не от A к

B,

16

а от B к A, то в разбиении T с
выбранными	точками			{M i }
изменилась	бы только		нумерация
отрезков и	точек	M i ,		а сама
интегральная сумма		не	изменилась
бы, поскольку в ее определении
фигурирует лишь длина ∆li участка,
которая не зависит от того, в каком
направлении	проходится			участок.
Это	означает,			что
∫ f (x, y)dl = ∫ f (x, y)dl .
AB	BA

В этом важнейшее отличие от обычного определенного интеграла, который менял бы знак при изменении направления обхода кривой.

Сформулируем теорему, сводящую новый пока объект - криволинейный

интеграл к обычному определенному интегралу.
Теорема.		Пусть f (M ) - непрерывная			на	кривой AB функция (т.е.
ε > 0 δ > 0 M1 , M 2 - точек кривой таких,					что расстояние между M1 , M 2
меньше δ,		f (M1 )− f (M 2 )		< ε ). Пусть кривая		AB параметризована так:
				′	′	- непрерывные на [T0 ;T1 ]
x = x(t), y = y(t),t [T0 ;T1 ], где x(t), y(t), x (t), y (t)

функции, причем каждому значению параметра соответствует единственная

				T1	′		2	′	2	dt .
точка кривой. Тогда ∫ f (M )ds = ∫ f (x(t), y(t)) (x (t))								+ (y (t))
			AB	T0
	Доказательство.				Интегральная						сумма
∑n	f (M i )∆li	= ∑n	f (M i )∫ti	(x′(t))2 +(y′(t))2 dt для		криволинейного					интеграла
i=1		i=1	ti −1
первого		типа		отличается	от	интегральной					суммы
∑ f (x(ti ), y(ti ))			(x′(ti ))2 + (y′(ti ))2 ∆ti			для					интеграла

17

T				t
∫1	f (x(t), y(t))	(x′(t))2 + (y′(t))2 dt лишь тем, что		∫i	(x′(t))2	+ (y′(t))2 dt несколько
T0				ti −1
отличается		от	(x′(ti ))2 + (y′(ti ))2 ∆ti , именно	,	этот	интеграл равен

(x′(ξi ))2 + (y′(ξi ))2 ∆ti .

Нетрудно доказать, что при d(T )→ 0 пределы этих сумм равны (строгое

доказательство опущено). Это означает, что теорема доказана.

Отметим, что изменение направления обхода кривой означает одновременную смену пределов интегрирования и знака величины dt, что не изменяет величину интеграла в правой части этого равенства.

Из свойств криволинейного интеграла отметим следующие 2 основных:

1.	∫(λ1 f1 (M )+ λ2 f2 (M ))dl = λ1 ∫ f1 (M )dl + λ2			∫ f2 (M )dl	при условии,	что
	AB		AB	AB
	существуют ∫ f1 (M )dl и ∫ f2 (M )dl .
		AB	AB
2.	Если	AB, BC -	кривые, удовлетворяющие		условиям теоремы,	то
	∫ f (M )dl = ∫ f (M )dl + ∫ f (M )dl .
	AC	AB	BC

Свойство 2 позволяет определить криволинейные интегралы 1-го типа для кусочно-гладких кривых (т.е. кривых, состоящих из конечного числа частей, каждая из которых удовлетворяет условиям теоремы). В частности, можно определить криволинейный интеграл и для замкнутых кривых.

2. Криволинейные интегралы второго типа

Рассмотрим, как и в параграфе 1, кривую AB, которую пока считаем незамкнутой.

18

Пусть проекция этой кривой на ось x представляет собой отрезок [a; b].

Пусть точки A0 ,..., An дают разбиение кривой AB. Рассмотрим их проекции x0 ,..., xn , лежащие на отрезке [a; b] и обозначим ∆xi = xi − xi−1 , i =1,..., n .

Пусть P(x, y) - определена на AB. Пусть M i -								точка, лежащая на кривой
					n	)∆xi .
между Ai−1 и Ai . Положим σ = ∑P(M i
					i=1
Определение. Пусть					I R . Если	ε > 0	δ > 0 T : d(T )<δ		и {Mi }
выполняется		σ − I		<ε ,	то говорят,	что I	- это	криволинейный	интеграл

второго типа ∫P(x, y)dx .

AB

Точно также, рассматривая проекции на ось y, определим ∫Q(x, y)dy .

AB

Интеграл общего вида ∫P(x, y)dx +Q(x, y)dy определяется, как сумма этих

AB

двух интегралов.

Вычисление криволинейного интеграла 2-го типа проводится в

соответствии со следующей теоремой.
Теорема. Пусть L – кривая, заданная уравнениями:	x = x(t)	, t [T ,T ],
	y = y(t)	0	1

P(x, y) и Q(x, y) – непрерывные на L функции. Тогда:

∫Pdx + Qdy = T∫1 (P(x(t), y(t))x′(t)+ Q(x(t), y(t))y′(t))dt .

L

T0

Теорема без доказательства.

Примечание 1.

19

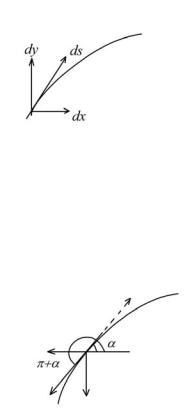
a) Если кривая L задана явным уравнением	y =φ(x), a ≤ x ≤ b ,	где φ(x) -
непрерывно дифференцируемая функция,	то предыдущая	формула

принимает вид: ∫Pdx +Qdy = ∫b P(x,φ(x))dx + ∫b Q(x,φ(x))φ′(x)dx .

L a a

b)	Если L	задана уравнением x =ψ(y), c ≤ y ≤ d , то ∫Pdx +Qdy =
			L
	d	′	d
	= ∫P(ψ(y), y)ψ (y)dy + ∫Q(ψ(y), y)dy .
	c		c
c)	Если L -	отрезок прямой x = x0 , то ∫Pdx ≡ 0 для любой функции P,
			L

если L - отрезок прямой y = y0 , то ∫Qdy ≡ 0 для любой функции Q.

L

Примечание 2.

Пусть	α - угол, составляемый	вектором касательной к кривой и
положительным направлением оси x.		Тогда dx = ds cosα, dy = ds sin α . Поэтому
∫Pdx +Qdy = ∫(P cosα +Q sin α)ds .
L	L

Заметим, что при изменении направления обхода угол α изменяется на π +α . При этом cos(π +α)= −cosα, sin(π +α)= −sin α , и интеграл в правой части написанного выше равенства меняет свой знак.

20