chirskii-lectures-4sem

обходе которого направление нормали при возвращении в исходную точку сменяется на противоположное, то поверхность называется односторонней.

Бываю поверхности, не являющиеся двусторонними. Простейший

A		B
E		F
D		C

пример – лист Мебиуса. Он получается так: рассмотрим прямоугольник ABCD и линию EF, соединяющую середины его сторон.

Склеим точку A с точкой с С, В с D.

Если обходить контур EF, то при возвращении в исходную точку направление нормали изменится на противоположное. Это

доказывает односторонность листа Мебиуса.

В дальнейшем мы будем рассматривать только двусторонние поверхности.

Двусторонняя поверхность, у которой выбрана сторона, называется ориентированной. На ориентированной поверхности определено положительное направление произвольного замкнутого контура, лежащего на ней, а также контура, ограничивающего саму эту поверхность. Пусть L – рассматриваемый контур и пусть ”обходчик”, голова которого направлена так же, как и выбранная нормаль к поверхности при обходе этого контура видит ограничиваемую этим контуром часть G рассматриваемой поверхности слева от себя (в случае, если обходчик пошёл по краю поверхности S, он должен видеть S слева от себя).

41

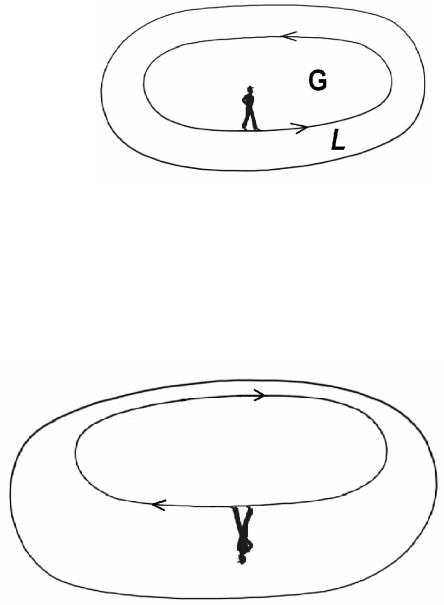
В этом случае контур обходится в положительном направлении. Противоположное направление считаем отрицательным.

Очевидно, что если взять другую сторону поверхности, т.е. изменить в данной точке направление нормали на противоположное, то положительное направление обхода контуров станет отрицательным и наоборот.

Стрелка указывает новое положительное направление обхода – оно совпадает с бывшим отрицательным.

42

4. Поверхностные интегралы II типа (II рода).

Пусть S — двусторонняя поверхность. Вначале считаем, что S задана

уравнением	z = z(x, y),			(x, y) D1 ,где D1		— квадрируемое		множество	на
плоскости	XOY. Как			обычно, считаем,		что	z(x, y), ∂z (x, y), ∂z (x, y)		—
							∂z	∂y
непрерывные на D1		функции, и выберем верхнюю нормаль к S.
Разобьем область				D1	на квадрируемые участки D1,i и выберем точки
(ξi ,ηi ) D1	произвольным образом. Пусть функция R(x, y,z)							определена на
поверхности S.
Рассмотрим интегральную сумму
		∑n−1	R(ξi ,ηi ,z(ξi ,ηi )) пл.(D1,i )= σ(R,T,{ξi ,ηi })
		i=0
Если I R		ε > 0			δ > 0 T : d(T)< δ		{ξi ,ηi }

σ(R,T,{ξi ,ηi })−I < ε,

то число I называется поверхностным интегралом II типа (II рода)

от функции f по внешней стороне S и обозначается так:

I = ∫∫R(x, y, z)dxdy .

S

(Часто используется более современное обозначение

I = ∫∫R(x, y, z)dx dy .)

S

Если выбрана нижняя сторона поверхности S, то все величины пл.(D1,i )

в интегральной сумме заменяем на (−пл.(Di,1 )).

Это означает, что поверхностный интеграл II типа (II рода) по нижней стороне поверхности отличается от интеграла по верхней стороне поверхности только знаком.

Как отмечалось выше, пл.(Si					)=	пл.(D1,i )
							cosγi
пл.(Di,1 )= пл.(Si )		cosγi		, т.е.

43

пл.(Di,1 )= пл.(Si )cosγi , если γi составляет с осью Z острый угол.

пл.(Di,1 )= −пл.(Si )cosγi			, если γi	составляет с осью Z тупой угол.
Поэтому, cosγi пл.(Si )= пл.(Di )				или − пл.(Di ),		в зависимости от выбора
стороны поверхности и ∫∫R(x, y, z)dx dy = ∫∫R(x, y, z)cosγdS .
	S				S
Точно также, если R(x, y,z) — непрерывная функция, то
∫∫R(x, y, z)dx dy = ∫∫R(x, y, z(x, y))dxdy , если взята верхняя сторона S и
S		D1
∫∫R(x, y, z)dx dy = −∫∫R(x, y, z(x, y))dxdy , если взята нижняя сторона S.
S		D1
Если	S задаётся	уравнением			y = y(x, z),	(x, z) D2 ,	квадрируемой
области плоскости xOz ,		то определён интеграл ∫∫Q(x, y, z)dz dx , который
						S
равен ∫∫Q(x, y, z)cos βdS .			Интеграл		∫∫Q(x, y, z)cos βdS вычисляется			по
S					S
формуле	∫∫Q(x, y(x, z), z)dxdz , если				угол, составляемый		нормалью	к
	S

выбранной стороне поверхности с осью y острый (то есть, угол β), и по формуле − ∫∫Q(x, y(x, z), z)dxdz , если этот угол тупой.

S
Если же	S задана	уравнением x = x(y, z),	(y, z) D3 , квадрируемой
области плоскости yOz ,		то определён интеграл	∫∫P(x, y, z)dy dz , равный
			S
∫∫P(x, y, z)cosαdS	и вычисляемый по формуле ∫∫P(x(y, z), y, z)dydz , если угол,
S		D3

составляемый нормалью к выбранной стороне поверхности с осью x острый,

и по формуле −∫∫P(x( y, z), y, z)dydz , если этот угол тупой.

D3

Если поверхность S можно одновременно представить уравнениями

рассмотренных	выше	типов,	то	определён
∫∫P(x, y, z)dy dz +Q(x, y, z)dz dx + R(x, y, z)dx dy = ∫∫P cosα +Q cos β + R cosγ)dS
S			S

44

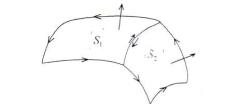
Если поверхность S есть конечное объединение таких поверхностей и

ориентации таких поверхностей согласованы, то интеграл по всей поверхности равен сумме интегралов по составляющим эту поверхность частям.

Согласованность ориентации означает следующее: нормали на отдельных частях выбраны так, что положительные направления обхода общих границ противоположны друг

другу.

Вобщем случае, если поверхность S задана параметрически:

x= x(u,v)

y= y(u,v)

z= z(u, v)

где

u,v ∆

- квадрируемой области и

x, y, z C1(∆) , то

∫∫P(x, y, z,)cosα dS +Q(x, y, z)cos β dS + R(x, y, z)cosγ dS =

S

= ±∫∫P(x(u,v), y(u,v), z(u,v)) A(u,v)dudv ± ∫∫Q(x(u,v), y(u,v), z(u,v)) B(u,v)dudv ±

∆

∆

± ∫∫R(x(u,v), y(u,v), z(u,v)) C(u,v)dudv

∆

где, как и выше,

A(u,v)=

∂y ∂z

,

B(u,v)=

∂z ∂x

,

C(u,v)=

∂x ∂y

,

∂u

∂u

∂u

∂u

∂u

∂u

∂y

∂z

∂z

∂x

∂x

∂y

∂v ∂v

∂v ∂v

∂v ∂v

ir

rj

kr

(то есть, коэффициенты нормали, равной

∂x

∂y

∂z

),

∂u

∂u

∂u

∂x

∂y

∂z

∂v

∂v

∂v

а знак “+” или “−” выбирается в соответствии с выбором стороны поверхности.

Пример. Приведём пример вычисления поверхностного интеграла 2-го

типа I = ∫∫xdy dz + ydz dx + zdx dy , где S – внешняя сторона сферы

S

45

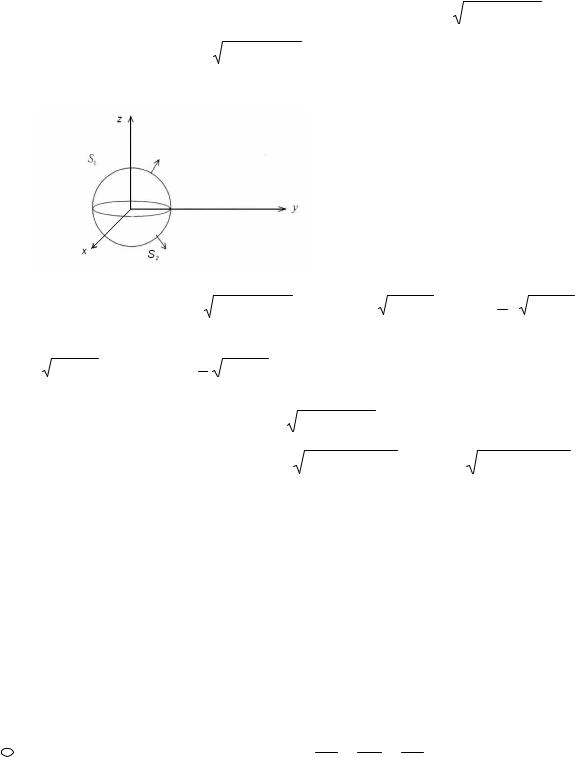
x2 + y2 + z2 = a2 . Обозначим I1 = ∫∫zdx dy . Из соображений симметрии

S

очевидны равенства ∫∫xdy dz = ∫∫ydz dx = I1 , так что I=3I1. Поверхность S

S S

состоит из частей S1 и S2, задаваемых уравнениями z = a2 − x2 − y2 (это S1 –

верхняя полусфера) и z = − a2 − x2 − y2 (это уравнение для нижней полусферы

S2). На S1 внешняя нормаль составляет с осью z острый угол, на S2 – тупой.

Поэтому ∫∫zdxdy = ∫∫

a2 − x2 − y2 dxdy =

2∫πdϕ∫ a2 −r 2 rdr = 2π

1

∫a

a2 −r 2 d(r 2 )=

S

D

0

2

0

1

= −π∫a

a2 −r 2 d (a2 −r 2 )= −π 2

( a2 −r 2 )2

a =

2πa3 .

0

3

0

3

Аналогично, так как на S2 z = −

a2 − x2 − y2 , а нормаль составляет с осью

z

тупой угол,

∫∫zdx dy = −∫∫−

a2 − x2

− y2 dxdy = ∫∫ a2

− x2 − y2 dxdy =

S2

D

D

=

2πa3

. Значит, I1

= ∫∫zdx

dy =

2πa3

+

2πa3

=

4πa3

. Поэтому I = 3I1 = 4πa3 .

3

S

3

3

3

5. Формула Остроградского-Гаусса.

Теорема. Пусть S – замкнутая кусочно-гладкая поверхность, ограничивающая тело V в пространстве. Пусть выбрана внешняя сторона S. Пусть P,Q,R – функции, имеющие непрерывные производные на V. Тогда

∫∫	(Pdy dz + Qdz dx + Rdx dy)=		∂P		∂Q		∂R
		∫∫∫		+		+
								dxdydz . Равносильная
S		V	∂x		∂y		∂z

46

формулировка:	∫∫	(Pcosα +Qcos β + R cosγ )dS =				∂P	+ ∂Q +	∂R		где
				∫∫∫
									dxdydz ,
	S			V		∂x	∂y	∂z
(cosα,cos β,cosγ ) − внешняя нормаль к S.
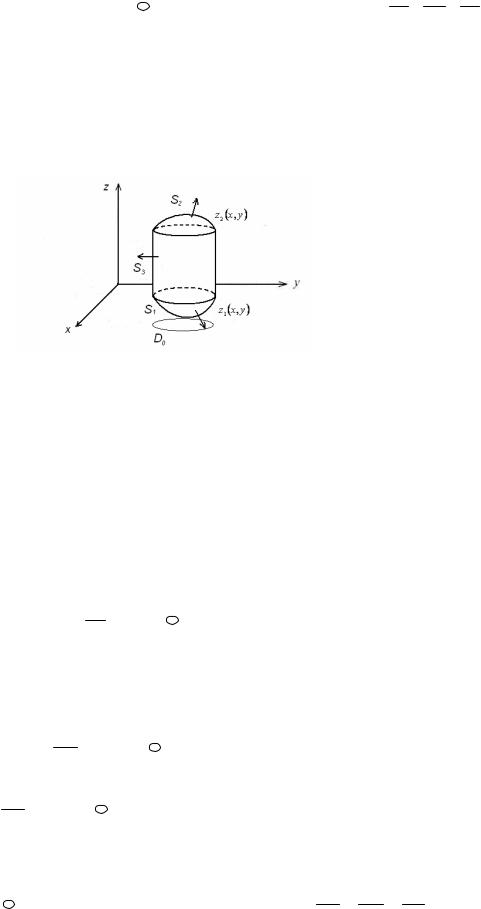
Доказательство. Предположим, что V ограничено сверху S2 – графиком
функции z = z2 (x, y),	снизу S1 z = z1(x, y),		x, y D0 , а сбоку –					цилиндрической

поверхностью S3.

Вычислим∫∫∫∂R dxdydz = ∫∫dxdy					z	(x,y)	∂Rdz = ∫∫(R(x, y, z2 (x, y))−R(x, y, z2
					2	∫					(x, y)))dxdy =
	V	∂z	D		z	(x,y)	∂z	D
			0		1			0
= ∫∫R(x, y, z2 (x, y))dxdy −∫∫R(x, y, z1 (x, y))dxdy = ∫∫Rdx dy −∫∫Rdx dy ,											так как на
D0			D0					S2	S1
S1 внешняя нормаль составляет с осью z тупой угол.
Далее,	на	S3	cosγ = 0	и		можно		добавить	к	сумме	слагаемое
0 = ∫∫R cosγ	dS = ∫∫Rdx dy .
S3	S3
Итак, ∫∫∫∂Rdxdydz = ∫∫Rdx dy .
	V ∂z		S
Далее,	если	поверхность		S		можно		представить	в	виде объединения

поверхностей

x = x2 (y, z), x = x1(y, z),

x, y D1 и цилиндрической поверхности,

то

∫∫∫

∂Qdxdydz = ∫∫Qdz dx ,

и,

при

аналогичных

условиях,

V

∂y

S

∫∫∫

∂Pdxdydz = ∫∫Pdy dz .

V

∂x

S

Поэтому, если поверхность S удовлетворяет условиям всех трёх случаев,

то

∫∫

(Pdy dz + Qdz dx + Rdx dy)=

∂P +

∂Q

+ ∂R

dxdydz .

∫∫∫

∂x

∂y

∂z

S

V

47

Теперь предположим, что V состоит из конечного числа тел V1,…,Vk, разделённых гладкими поверхностями S1,…,Sk, причём эти тела Vi удовлетворяют сформулированным выше условиям. Для простоты, пусть

V =V1 V2 , S = S1 S2 :

Тогда:

∂P + ∂Q

+ ∂R

∂P

+ ∂Q +

∂R

∂P + ∂Q

+ ∂R

Каждый

dxdydz =

dxdydz +

dxdydz .

∫∫∫

∂x ∂y

∂z

∫∫∫

∂x

∂y

∂z

∫∫∫

∂x ∂y

∂z

V

V

V

1

2

из

интервалов

∂P

∂Q + ∂R

преобразуем по

формуле

∫∫∫

+

i =1,2 ,

dxdydz ,

V

∂x

∂y

∂z

1

Остроградского-Гаусса

как

∫∫(Pdy dz + Qdz dx + Rdx dy), i =1,2 , где

Si

взяты внешние стороны поверхностей Si, i =1,2 .

Поверхности S1 и S2 имеют общую часть

~

, причём их внешние нормали

S

~

~

Pdy dz + Qdz dx + Rdx dy

на S противоположны и интегралы по

S от

взаимно сократятся, поэтому ∫∫Pdy dz + Qdz dx + Rdx dy +

S1

+ ∫∫Pdy dz + Qdz dx + Rdx dy = ∫∫Pdy dz + Qdz dx + Rdx dy .

S2

S

Тем самым, теорема доказана.

6. Формула Стокса.

Теорема. Пусть S – гладкая ориентированная двусторонняя поверхность (т.е. направление нормали выбрано) и L – кусочно гладкая кривая, ограничивающая S, причём мы считаем направление обхода L положитель-

48

ным. Пусть функции

P,Q, R –

непрерывно

дифференцируемые. Тогда

∫

(Pdx +Qdy + Rdz)=

∂R

∂Q

∂P ∂R

∂Q

∂P

∫∫

−

−

dz

−

dy dz +

dx +

dx dy .

L

S

∂y

∂z

∂z

∂x

∂x

∂y

Замечание

1.

Равносильная

формулировка

∫

(Pdx +Qdy + Rdz)=

∂R

∂Q

∂P ∂R

∂Q

∂P

∫∫

−

+

−

−

cosα

cos β +

cosγ dS .

L

S

∂y

∂z

∂z

∂x

∂x

∂y

Замечание 2. В случае плоской кривой L, лежащей на плоскости Oxy и функций P(x, y), Q(x, y) эта формула совпадает с формулой Грина.

Замечание 3. Формулы в правой части запомнить непросто. Поэтому удобно записать подынтегральное выражение в виде определителя:

cosα			cos β			cosγ
	∂			∂			∂		.
	∂x			∂y			∂z
	P			Q			R

Разумеется, это не совсем обычный определитель. Ведь во второй строке его стоят операторы дифференцирования. Поэтому условимся считать, что мы понимаем под этим определителем его формальное разложение по первой

строке, причём произведение, например, оператора ∂∂x на функцию R есть

	∂R	и т.п.
	∂x
		Доказательство.		Вычислим, например, ∫Pdx . Пусть, для простоты,
					L
				z = z(x, y) - уравнение S.
				Тогда	рассмотрим	параметризацию
				проекции	l кривой L на	плоскости	z = 0 :
				x = x(t), y = y(t), t [T0 ;T1 ] (разумеется, x(t) , y(t)
				- непрерывно дифференцируемые функции).
			T1	′
		Тогда ∫Pdx = ∫P(x(t), y(t), z(x(t), y(t)))x dt = ∫P(x, y, z(x, y))dx . К плоской кривой l
		L	T0		l
применим формулу				Грина: ∫P(x, y, z(x, y))dx = −∫∫ ∂ P(x, y, z(x, y))dxdy , где			D –
				l	D ∂y

49

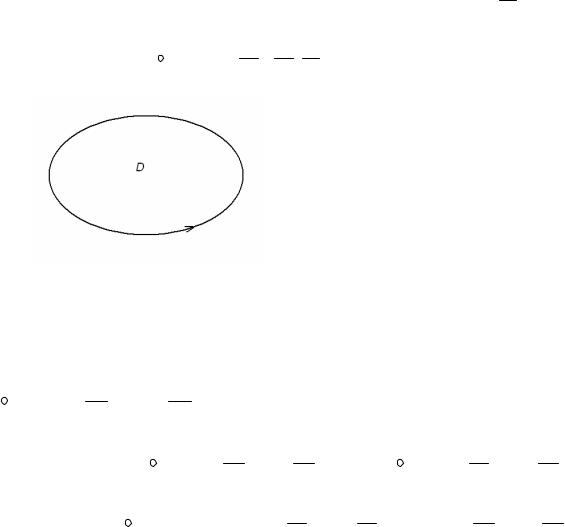
ограничиваемая кривой

	=	∂P	+	∂P		∂z	. Итак,	∫Pdx
		∂y		∂z		∂y
								l

l область плоскости Oxy. Вычислим ∂∂y P(x, y, z(x, y))=

∂P ∂P ∂z

=−∫∫D ∂y + ∂z ∂y dxdy .

Перейдём от двойного интеграла к поверхностному: dxdy = cosγdS ,

∂z	cosγ = −cos β , и значит,	∂z dxdy =	∂z cosγdS = −cos βdS . Поэтому
∂y		∂y	∂y

	Pdx =		∂P cos β −
∫				∂P cosγ dS .
		∫∫	∂z	∂y
l		S

Аналогично,

∫

∂Q cosγ − ∂Q cosα

,

∫

∂R cosα −

Qdy =

∫∫

Rdz =

∫∫

dS

∂R cos β dS

L

S

∂z

∂y

l

S

∂y

∂x

и

∫

(Pdx +Qdy + Rdz)=

∂P

∂P

∫∫

∂Q

∂Q

∫∫

cos β −

cosγ

cosγ −

cosα +

∂z

∂y

dS +

∂z

L

S

S ∂x

∂R

∂R

∂R ∂Q

∂p ∂R

∂Q ∂P

+

∫∫

cosα −

∫∫

−

−

cos β

−

cos β dS =

cosα +

+

cosγ dS .

S

∂y

∂x

S

∂y

∂z

∂z

∂x

∂x

∂y

Формула Стокса доказана.

Введение в теорию дифференциальных форм.

В трёхмерном пространстве определены следующие внешние дифференциальные формы:

ω1 = Pdx +Qdy + Rdz (форма первой степени)

ω2 = Rdx dy +Qdz dx + Pdy dz (форма второй степени)

Здесь и выше P, Q и R – функции от x, y и z.

ω3 = dx dy dz (ориентированный элемент объёма)

Операция , называемая внешним произведением, обладает такими свойствами: 1) (dx dy) dz = dx (dy dz)

50