chirskii-lectures-4sem

2) dx dy = −dy dx

Для дифференциальной формы определено дифференцирование, обладающее свойствами:

1) d(ω1 +ω2 ) = dω1 + dω2

2)d( (ω1 ω2 ) = dω1 dω2 + (−1)k ω1 dω2 , где k – степень формы ω2

3) d(dω) = 0

Следуя этим правилам, вычислим: d(Pdx) = dP dx + Pd( fx) = dP dx , т.к. P –

формулой нулевой степени. Например,

dω1 = d(Pdx +Qdy + Rdz) = d(Pdx) + d(Qdy) +

=dP dx + dQ dy + dR dz = ∂∂P dx + ∂∂P dy

x y

d(Rdz) =

+ ∂∂P dz dx + z

	∂Q		∂Q		∂Q
+		dx +		dy +		dz
	∂x		∂y		∂z

	∂R		∂R		∂R
dy +		dx +		dy +		dz dz =
	∂x		∂y		∂z

=∂∂Px dx dx + ∂∂Py dy dx + ∂∂Pz dz dx + ∂∂Qx dx dy + ∂∂Qy dy dy + + ∂∂Qz dz dy + ∂∂Rx dx dz + ∂∂Ry dy dz + ∂∂Rz dz dz =

=− ∂∂P dx dy + ∂∂P dz dx + ∂∂Q dx dy + ∂∂R dy dz + − ∂∂Q dy dz + − ∂∂R dz dx =y z x y z x

∂Q

∂P

∂P

∂R

∂R

∂Q

=

−

dx dy +

−

x dz dx +

−

dy dz

∂x

∂y

∂z

∂y

∂y

∂z

Полученный результат даёт повод вспомнить теорему Стокса.

Далее,

d(ω2 ) = d(Rdx dy + Qdz dx + Pdy dz) = dR dx dy +

∂R

∂R

∂R

+ dQ dz dx + dP dy dz =

dx +

dy +

dz

dx dy

+

∂x

∂y

∂z

∂Q

∂Q

∂Q

∂P

∂P

∂P

+

dx +

dy +

dz

dz dx +

dx +

dy +

dz

dy dz =

∂x

∂y

∂z

∂x

∂y

∂z

= ∂∂Rx dx dx dy + ∂∂Ry dy dx dy + ∂∂Rz dz dx dy + ∂∂Qx dx dz dx +

51

+∂∂Qy dy dz dx + ∂∂Qz dz dz dx + ∂∂Px dx dy dz +

+∂∂P dy dy dz + ∂∂P dz dy dz = ∂∂P + ∂∂R + ∂∂Q dx dy dz y z x z y

так как dz dx dy = −dx dz dy = dx dy dz .

Полученный результат даёт повод вспомнить теорему Остроградского.

52

Приложения кратных, криволинейных и поверхностных интегралов. Элементы теории поля.

1. Скалярное и векторное поле

Определение. Скалярное поле на области D R 3 ( D R 2 ) представляет собой произвольную функцию U (M ), определенную на D, M D .

Поверхности уровня скалярного поля – это множества решений уравнения U (M )= C, C R при заданных значениях C .

Пример. На географической карте линии уровня (двумерный аналог поверхности уровня) показывают точки, лежащие на одной высоте. Аналогичные примеры – изотермы, изобары и т.д.

Векторное поле F на области D R 3 (или D R 2 ) – это вектор, координаты которого (P, Q, R) являются функциями, определенными на D .

Примеры представляют собой силовое поле, поле скоростей и т.п.

2.Производная скалярного поля по направлению. Градиент скалярного поля

Во 2-м семестре мы уже рассматривали производную плоского поля (т.е.

	D R 2 ) по направлению l ,	∂U	. Понятие величины отрезка M 0 M
		∂l

определяется аналогично и для D R 3 . Напоминаем: величина M 0 M отрезка

M 0 M представляет собой его длину со знаком “+”, если векторы M 0 M и l

одинаково направлены и длину со знаком “-”, если их направления

противоположны. Тогда, по определению, ∂U =	lim	U (M )−U (M 0 )	.
∂l	M →M 0	M 0 M

53

gradU (M 0 )

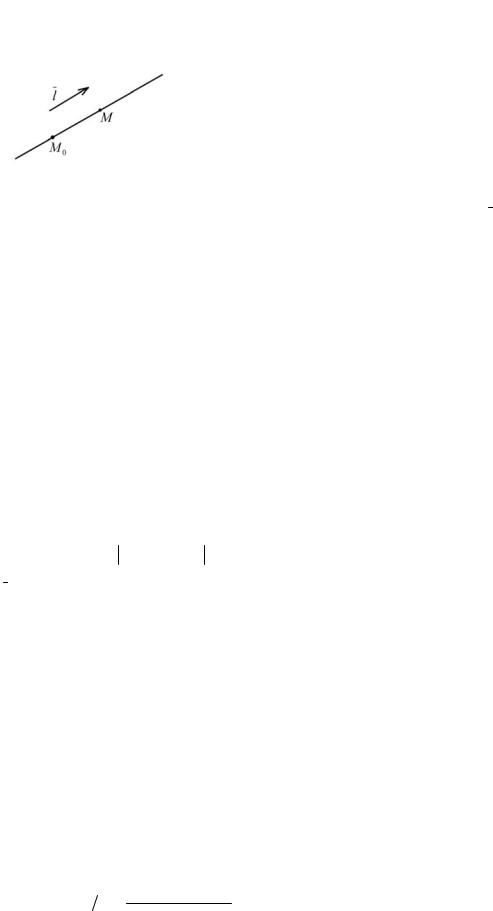
Если

введена система прямоугольных

декартовых координат и вектор

задан

l

направляющими косинусами (cosα, cos β, cosγ ),

то при условии дифференцируемости U

в т.

M 0 легко вывести формулу:

∂U

(M 0 )=

∂U

(M 0 )cos

α +

∂U

(M 0 )cos β +

∂U

(M 0 )cosγ = (gradU , l

),

где

∂x

∂l

∂y

∂z

∂U

∂U

∂U

gradU (M 0 )

=

(M 0 ),

(M 0 ),

(M 0 ) - градиент скалярного поля U в точке

∂x

∂y

∂z

M 0 .

Разумеется, понятие градиента можно ввести и без использования

системы

координат:

∂U

gradU

cosφ =

gradU

cosφ , т.к.

- единичный

=

l

l

∂l

∂U

вектор.

Таким образом,

≤

gradU

, причем равенство

наступает при

∂l

∂U

условии

cosφ

=1. Наибольшее

значение

по всем выборам

, таким

l

∂l

образом, есть grad(U (M 0 )) , а направление градиента – это как раз тот вектор l , на котором это наибольшее значение достигается. Итак, направление и модуль вектора определено без использования координат. Это

говорит об инвариантности этого понятия и о наличии реальных естественнонаучных интерпретаций.

Однако для вычисления градиента удобно его координатное представление. Из него, в частности, легко следуют свойства градиента.

1.grad(u + v)= gradu + gradv

2.grad(c u)= cgradu, c = const

3.grad(u v)= ugradv + vgradu

4.grad(u v)= vgradu − ugradv , v ≠ 0

v2

5.gradf (u)= f ′(u)gradu ( f - дифференцируемая функция)

54

Пример.

Найдем gradr ,

где

r = r =

x2

+ y 2

+ z 2

- модуль радиус-вектора

(x, y, z).

r

∂r =

x

,

∂r

=

y

,

∂r

=

z

и

dx

x2 + y 2 + z 2

∂y

x2 + y 2 + z 2

∂z

x2 + y 2 + z 2

x

y

z

r

.

gradr =

,

,

=

r

r

r

r

По формуле 5 из этого равенства следует: gradf (r)= f ′(r) rr

Мы получили формулу для вычисления градиента радиальной функции

f (r).

Рассмотрим теперь поверхность уровня скалярного поля U , т.е. поверхность, задаваемую уравнением U (x, y, z)= C . Предположим, что U -

непрерывно дифференцируемая функция от x, y, z . Тогда уравнение касательной плоскости в точке M 0 , лежащей на этой поверхности, имеет вид

∂U	(M 0 )(x − x0 )+	∂U	(M 0 )(y − y0 )+	∂U	(M 0 )(z − z0 )= 0 .
∂x		∂y		∂z

Координаты вектора градиента представляют собой коэффициенты этого уравнения. Поэтому gradU (M 0 ) - нормаль к касательной плоскости в т. M 0 и,

по определению, нормаль к самой поверхности уровня в этой точке.

3. Поток вектора через поверхность. Дивергенция векторного поля. Векторная формулировка теоремы ОстроградскогоГаусса

Пусть F - векторное поле, S - двусторонняя поверхность. Пусть выбрана

сторона, т.е. нормаль n . Назовем ∫∫(F n)dS - потоком вектора F через

S

поверхность S в указанную сторону.

55

S

dt∫∫F n dS . Таким образом, поток

F n dS dt .

Этот термин совпадает со следующей гидродинамической задачей. Пусть F - вектор скорости течения жидкости в момент t . Посчитаем, сколько жидкости пройдет через малую часть поверхности dS за момент времени dt . Этот объем жидкости представляет собой цилиндр с основанием dS и высотой F n dt , т.е.

этот объем равен Тогда для всей поверхности получим

представляет собой скорость изменения количества протекающей через S жидкости в рассматриваемый момент времени.

Пусть векторное поле

F

задано в

выбранной

системе

координат

как

(P, Q, R). Назовем дивергенцией

скалярное поле div

=

∂P

+

∂Q

+

∂R

(при

F

F

F

∂y

∂z

∂x

условии, что эти частные производные существуют).

Легко доказать, что:

1. div(

+

)= div

+ div

a

b

a

b

2. div(U

)=Udiv

+

gradU .

Здесь

U

-

скалярное

поле и символ

gradU

a

a

a

a

обозначает скалярное произведение этих векторов.

Вспомним

формулировку

теоремы

Остроградского-Гаусса:

∂P

∂Q

∂R

(P cosα +Qcos β + R cosγ )dS =

F = (P, Q, R)

∫∫

+

+

dxdydz ,

где

-

∫∫∫

∂x

∂y

∂z

S

V

непрерывно дифференцируемое векторное поле, S - замкнутая поверхность,

ограничивающая объем V и (cosα, cos β, cosγ ) - вектор внешней нормали.

Левая часть формулы имеет вид ∫∫(

)dS , т.е. представляет собой поток

F

n

S

через внешнюю сторону S ,

а правую часть можно выразить следующим

F

56

образом:	∫∫∫div		Fdxdydz . Итак, векторная				формулировка теоремы
	V
Остроградского-Гаусса:
При сформулированных выше условиях ∫∫(							)dS = ∫∫∫div		Fdxdydz .
				F		n
			S				V

Понятие divF можно определить независимым от координат способом.

Для этого рассмотрим точку M 0 , окружим ее шаром радиуса ε							и применим
теорему Остроградского-Гаусса: ∫∫(				)dS = ∫∫∫div		Fdxdydz ,	где Vε -
	F		n
Sε				Vε

вышеупомянутый шар, а Sε - внешняя сторона ограничивающей его сферы. К

правой части применим теорему о среднем (учитывая непрерывность divF ):

∫∫∫div

Fdxdydz = div

(M1 )

4

πε3 ,

где

M1

- близкая

к

M 0 точка.

При ε → 0

F

Vε

3

div

(M1 )→ div

(M 0 )

и

мы

можем

определить

дивергенцию

равенством:

F

F

∫∫(

)dS

(M0 )= lim

F

n

div

Sε

,

в правой

части которого

система

координат не

F

ε→0

4 3πε3

фигурирует.

Если считать

вектором скорости жидкости,

то div

-

это плотность

F

F

< 0 .

источника, если divF

> 0 , или стока, если divF

4. Соленоидальное поле

Определение. F - соленоидальное поле, если divF = 0 .

Векторная линия обладает тем свойством, что в любой ее точке вектор касательной к линии совпадает с F .

Векторная трубка – это совокупность векторных линий.

57

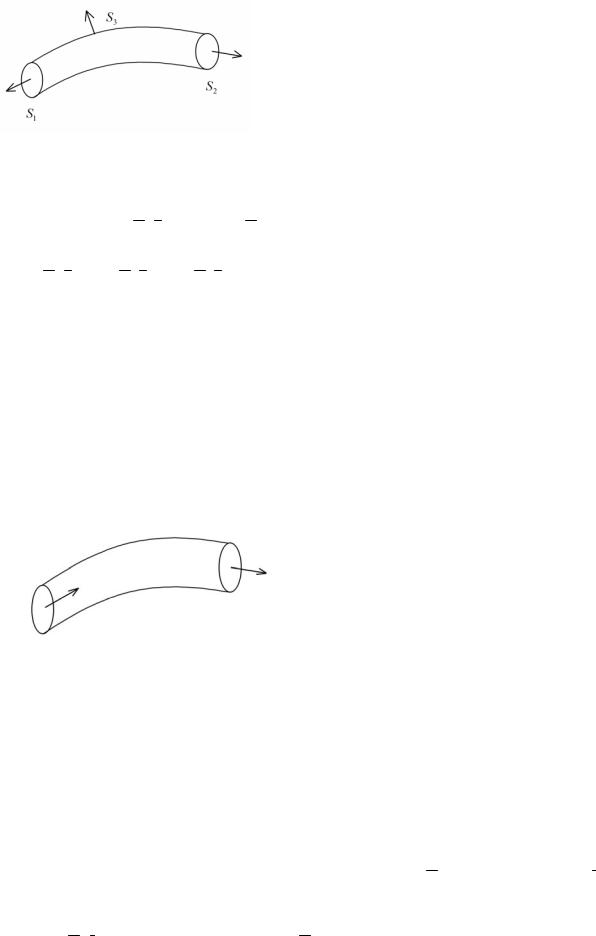
Пусть S1, S2 - сечения векторной трубки и S3	- ее боковая поверхность.
S = S1 US2 US3 . Рассмотрим внешнюю нормаль к	S и применим теорему

Остроградского: ∫∫F n dS = ∫∫∫divFdxdydz = 0 , в случае соленоидального поля.

S V

Итак, ∫∫F ndS + ∫∫F ndS + ∫∫F ndS = 0 . На S3 по определению векторной линии

S1 S2 S3

= 0 , поэтому ∫∫

или − ∫∫

F

n

F

ndS + ∫∫F ndS = 0

F

ndS = ∫∫F ndS . Изменяя

S2

S1

S1

S2

направление нормали на S1 на противоположное получаем, что поток соленоидального поля через поперечные сечения векторных трубок постоянен.

5. Циркуляция, ротор. Векторная формулировка теоремы Стокса

Пусть L - контур с заданным направлением обхода, F - векторное поле, l - единичный вектор касательной к кривой. Определим циркуляцию как

интеграл ∫(F l)dl (смысл – работа силы F вдоль контура L ).

L

58

Введем систему координат. Пусть

(cosα0 , cos β0 , cosγ 0 ) -

направляющие

косинусы

, (P, Q, R) - координаты

.

l

F

Тогда

(

)dl = (P cosα0

+ Q cos β0 + R cosγ 0 )dl = Pdx + Qdy + Rdz =

и

F

l

Fd r

циркуляция представляет собой интеграл ∫Pdx + Qdy + Rdz .

L

Для заданного непрерывно-дифференцируемого поля

(P, Q, R)

определим

F

ротор (или вихрь) этого поля:

∂R

∂Q

∂P

∂R

∂Q

∂P

−

,

−

,

−

rotF =

∂y

∂z

∂z

∂x

∂x

∂y

.

Легко проверить свойства ротора.

1.

rot(

+

)= rot

+rot

a

b

a

b

2.

rot(U

)=Urot

+ gradU ×

,

где

под

gradU ×

понимаем

векторное

a

a

a

a

произведение.

Вспомним

теперь

теорему

Стокса:

∫

∂R ∂Q

∂P ∂R

∂Q ∂P

Pdx

+ Qdy + Rdz =

∫∫

−

−

dz dx

−

∂y

dy dz +

∂z

+

∂x

∂y

dx dy

L

S

∂z

∂x

, где P, Q, R - непрерывно дифференцируемые функции,

S

- кусочно-гладкая

поверхность, L - ее край, причем направление обхода L относительно

выбранной стороны S является положительным.

Вспомним,

что

dy dz = cosαdS ,

dz dx = cos βdS ,

dxdy = cosγdS ,

где

cosα, cos β, cosγ - направляющие косинусы к выбранной стороне.

∂R

∂Q

−

При этом правая часть формулы Стокса принимает вид ∫∫

∂y

∂z

cosα +

S

∂P ∂R

∂Q

∂P

∫∫

(rotF n)dS . Итак,

+

−

cos β

+

−

cosγ dS или

в сделанных выше

∂z

∂x

∂x

∂y

S

предположениях теорема Стокса выглядит так:

∫Fd r = ∫∫(rotF n)dS .

L

S

Получим определение rot

без использования системы координат. Пусть

F

M 0 -

точка,

Sε

- плоскость,

в которой лежит окружность

Lε

радиуса

ε с

центром в M 0 .

59

Тогда

∫∫(rot

)dS = rot

(M1 )

(M1 ) πε 2

по

F

n

F

n

(Sε

)

теореме о среднем ввиду непрерывности

подынтегральной функции. Здесь точка M1

близка

к

M 0 . По теореме Стокса,

∫(

)dl = (rotF(M1 )

(M1 )) πε 2 или

F

l

n

Lε

∫(

)dl

F

l

rot

(M 0 )

(M 0 )= lim Lε

.

F

n

πε 2

ε→0

Ввиду произвольности выбора плоскости, получаем проекцию rotF(M 0 ) на произвольную ось n(M 0 ). Это определяет и сам вектор.

Легко вычислить, что rot gradU = 0 .

Можно доказать и обратное. Если область односвязная и векторное поле

F удовлетворяет условию rotF = 0 , то F - потенциальное, т.е. существует функция U такая, что F = gradU .

Отметим, что выводы о независимости интеграла от формы пути интегрирования, сделанные для двумерного случая, полностью переносятся и

	на трехмерный. Полученное там условие	∂Q	=	∂P	и rot		= 0 вполне
						F
		∂x		∂y
	аналогичны.

60