§3. Взаимное расположение двух прямых на плоскости.

Пусть две прямые на плоскости заданы общими уравнениями:

l₁: A₁x + B₁y + C₁ = 0 ,

l₂: A₂x + B₂y + C₂ = 0 .

Тогда мы сразу можем сделать вывод, что n1;\s\up8(( (A₁, B₁) и n2;\s\up8(( (A₂, B₂) – это векторы нормали к l₁ и l₂.

Теорема 2. 1. l₁||l₂  =  .

2. l₁= l₂  = = .

3. l₁ l₂  A₁A₂ + B₁B₂ = 0.

4. угол между l₁ и l₂ вычисляется по формуле

cos  = = . (16)

Доказательство. 1, 2. Очевидно, что прямые параллельны или совпадают тогда и только тогда, когда их векторы колинеарны, а по второму признаку коллинеарности векторов это равносильно

= =  . (_*)

При этом, прямые будут совпадать  у них есть общая точка M_o(x_o, y_o), т. е. если одновременно выполняется

A₁x_o + B₁y_o + C₁ = 0,

A₂x_o + B₂y_o + C₂ = 0.

Вычтем из первого равенства второе, домноженное на  :

(A₁– A₂)x_o + (B₁– B₂)y_o + C₁– C₂ = 0.

В силу (_*) обе скобки равны нулю  C₁– C₂ = 0  C₁/C₂ = . (_**) Объединяя (_*) и (_**), получаем требуемый результат.

Обратно, если выполнено условие пункта 2, то уравнения прямых l₁ и l₂ пропорциональны, т.е., разделив первое уравнение на некоторое число , мы получим второе уравнение. Значит, эти уравнения равносильны и определяют на плоскости одно и то же множество.

3, 4. Напомним, что углом между двумя прямыми называется меньший из двух углов, которые образуются при их пересечении. Таким образом, угол  между прямыми находится в пределах 0 /2. Пусть  –

угол между векторами нормали. Тогда 0 .

О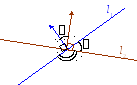чевидно, что совпадает с одним из двух углов, которые образуют прямые при пересечении.

1 случай: 0 /2. Тогда = 

cos  = cos  = ^.

2 случай: /2< . Тогда =– и cos  < 0 

cos  = cos ( – ) = – cos  =

= cos  = ^.

Эта формула подойдет и к первому случаю:

неотрицательная величина от модуля не изменится. Последнее равенство в (16) – эта та же формула, только расписанная в координатах. В частности, из (16) следует, что l₁ l₂  n1;\s\up8(( ·n2;\s\up8(( = 0  A₁A₂ + B₁B₂ = 0.

Упражнение. Самостоятельно напишите условия параллельности и совпадения двух прямых, заданных уравнениями с угловым коэффициентом.

Теорема 3. Пусть две прямые на плоскости заданы уравнениями с угловым коэффициентом

l₁: y = k₁x + q₁, l₂: y = k₂ x + q₂.

Тогда угол между ними вычисляется по формуле

tg  = .

Принимаем эту теорему без доказательства.

§4. Уравнение прямой в нормальной форме. Расстояние от точки до прямой.

Определение. Говорим, что общее уравнение прямой

Ax + By + C = 0 , (14)

имеет нормальную форму, если A²+B ² = 1. Это равносильно тому, что вектор n;\s\up8(((A, B) – единичный.

Если уравнение (14) не имеет нормальной формы, то мы можем привести его к этой форме, разделив на :

x + y + = 0.

Тогда ² + ² = 1.

Теорема 4. Пусть прямая l определяется уравнением (14) в нормальной форме. Тогда расстояние от точки M(x₁, y₁) до прямой вычисляется по формуле

h =Ax₁+ By₁+ C . (17)

С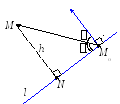ледствие. Если прямая задана произвольным уравнением вида (14), то

h = . (17 )

Доказательство. Пусть n;\s\up8(((A, B) – вектор нормали к l. Поскольку уравнение имеет нормальную форму, то n;\s\up8(( = 1. Пусть M_o(x_o, y_o) – произвольная точка на прямой. Опустим перпендикуляр MN на прямую l . Пусть  =( n;\s\up8((, MoM;\s\up10( –(),  =MM_oN .

1 случай. Точка M и вектор n;\s\up8(( лежат в одной полуплоскости относительно прямой l. Тогда

h =MN=MM_o·sin  =MoM;\s\up10( –(·sin( – ) =MoM;\s\up10( –(·cos ·n;\s\up8((= MoM;\s\up10( –( · n;\s\up8((

(мы домножили на n;\s\up8((, поскольку эта величина равна единице). Находим, что MoM;\s\up10( –( (x₁– x_o, y₁– y_o) 

h = A(x₁– x_o) + B(y₁– y_o) = Ax₁+By₁+C – (Ax_o+By_o+C)

(мы добавили и отняли C ). Поскольку M_o l, то выражение в скобках равно нулю, и мы получаем

h = Ax₁+ By₁+ C.

2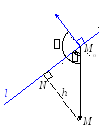случай. Точка M и вектор n;\s\up8(( лежат в разных полуплоскостях относительно прямой l. Тогда  =  – /2  sin  = – cos  и те же самые вычисления дают

h = – MoM;\s\up10( –( · n;\s\up8(( = –Ax₁ – By₁ – C.

Поскольку h – это расстояние, то h  0. Это

значит, что во втором случае Ax₁+By₁+C<0 (равенство исключается, т.к. M l). Поэтому

h =Ax₁+ By₁+ C .

Эта формула подойдет и к первому случаю.

Попутно мы выяснили, что знак выражения Ax₁+ By₁+ C зависит от того, в какой полуплоскости находится точка M. Это позволяет для двух данных точек M₁, M₂ выяснить, лежат ли они в одной полуплоскости относительно прямой l или в разных ( пересекает отрезок M₁M₂ прямую l или нет).