§12. Примеры решения задач.

1. Даны координаты вершин A(1,– 6), B(–3, 0), C(6, 9) треугольника ABC. Составить уравнение окружности описанной вокруг треугольника.

Р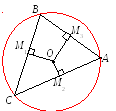ешение. Для того, чтобы составить уравнение окружности нам необходимо знать ее радиус R и координаты центра О(a, b). Тогда уравнение выглядит так:

(x–a)² +(y–b)² = R².

Центр окружности, описанной вокруг треугольника находится на пересечении серединных перпендикуляров к сторонам этого треугольника. Находим координаты середин M₁(x₁, y₁), и M₃(x₃, y₃) сторон BC и AB соответственно:

x₁= = = , y₁= = = , M₁ .

Аналогично m3(–1,–3).

Пусть l₃ – прямая, являющаяся серединным перпендикуляром к AB , а l₁ – к BC. Тогда n3;\s\up8(( = AB;\s\up10( –( (– 4, 6)  l₃ и l₃ проходит через M₃ . Поэтому ее уравнение:

– 4(x+1)+6(y+3) = 0.

Аналогично n1;\s\up8(( = BC;\s\up10( –( (9, 9)  l₃ . Поэтому уравнение l₁:

9(x)+9(y)=0,

x + y – 6 = 0.

Имеем О = l₁  l₃. Поэтому, чтобы найти координаты точки О необходимо решить совместно уравнения l₁ и l₃:

Прибавим ко второму уравнению первое, умноженное на 4:

Отсюда y = 1, x = 5, O(5, 1).

Радиус равен расстоянию от О до любой из вершин треугольника. Находим:

R =AO;\s\up10( –(= = .

Значит уравнение окружности:

(x – 5)² + (y –1)² = 65.

2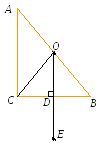.В прямоугольном треугольнике ABC известны уравнение одного из катетов 3x – 2y + 5 = 0, координаты вершины C(–5,–5) и координаты середины O(^– 3/2,–3) гипотенузы AB. Найти

координаты вершин A, B и координаты точки E, симметричной O относительно стороны BC. Найти координаты точки пересечения медиан треугольника ABC .

Решение. Пусть катет, уравнение которого нам дано, – это СВ. Он задан общим уравнением вида

ax+by+c=0.

В данном уравнении геометрический смысл

коэффициентов a и b – это координаты вектора нормали n;\s\up8(((a, b). Поэтому n;\s\up8(((3,2)ВС.

Составим уравнение перпендикуляра l = OD к стороне СВ и найдем координаты точки D. Вектор n;\s\up8(( будет параллелен OD, т.е. он является направляющим вектором этой прямой. Кроме этого, нам известны координаты точки О на этой прямой. Составляем параметрическое уравнение l:

(_*)

Имеем D = l  BC. Поэтому, для того, чтобы найти координаты этой точки мы должны решить совместно уравнения l и BC. Подставляем x и y из уравнения l в уравнение BC :

^3(– + 3t) –2(–3 2t)+5 = 0,

^–+ 9t +6 +4t+5 = 0,

13t=^– , t_D = ^– .

Подставляем найденное t в уравнение l и находим координаты точки D(–3,–2). Для того, чтобы найти координаты E вспомним физический смысл параметрического уравнения прямой: оно задает прямолинейное и равномерное движение. В нашем случае, начальная точка – это О, вектор скорости – это n;\s\up8((. Отрезок ОE вдвое длиннее отрезка ОD. Если за время t_D = ^– мы прошли путь от О до D, то путь от О до E мы пройдем за время t_E = 2t_D = –1. Подставляя это значение в (_*), находим E(– 4,5;–1).