§5. Уравнение плоскости в пространстве. Расстояние от точки до плоскости.

П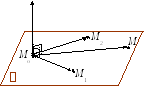лоскость в пространстве можно задать

а) с помощью точки M_o  и ненулевого вектора n;\s\up8(( ; тогда можем написать, что  ={M MoM;\s\up10( –(n;\s\up8((}; (_*)

б) с помощью точки M_ol и двух неколлинеарных векторов a;\s\up8(( и b;\s\up9((, параллельных ;

в) с помощью трех точек M_o, M₁, M₂ , не лежащих на одной прямой.

Теорема 5. 1. Плоскость , проходящая через точку M_o(x_o, y_o, z_o), перпендикулярно вектору n;\s\up8(((A, B, C), задается в декартовой СК уравнением

A(x – x_o) + B(y – y_o) + C(z – z_o) = 0. (21 )

2. Плоскость , проходящая через точку A_o(x_o, y_o, z_o), параллельно двум неколлинеарным векторам a;\s\up8(( и b;\s\up9(( задается уравнением

=0 (22)

3. Плоскость , отсекающая на координатных осях ненулевые отрезки a, b, c задается уравнением

+ + = 1 (23)

(предполагается, что a, b, c могут быть отрицательными).

Доказательство. 1. Пусть M(x, y, z) – произвольная точка плоскости. Тогда MoM;\s\up10( –( n;\s\up8((  MoM;\s\up10( –( · n;\s\up8(( = 0. Поскольку MoM;\s\up10( –((x–x_o, y–y_o, z–z_o), то последнее равенство в координатах как раз имеет вид (22).

Обратно, если координаты точки M(x, y, z) удовлетворяют (21), то MoM;\s\up10( –(n;\s\up8((  M.

2. Пусть M(x, y, z) – произвольная точка плоскости. Тогда MoM;\s\up10( –( компланарен векторам a;\s\up8(( и b;\s\up9((, а это равносильно тому, что смешанное произведение этих трех векторов равно нулю: MoM;\s\up10( –( a;\s\up8(( b;\s\up9(( = 0. В координатах последнее равенство как раз имеет вид (22).

О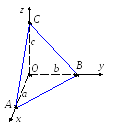братно, если координаты точки M(x, y, z) удовлетворяют (22), то векторы MoM;\s\up10( –(, a;\s\up8((, b;\s\up9(( компланарны, а значит M.

3. Условие означает, что плоскость проходит через точки A(a, 0, 0), B(0, b, 0), C(0, 0, c). Векторы AB;\s\up10( –((a, b, 0) и AС;\s\up10( –((a, 0, c) параллельны плоскости. Подставим их координаты в (23):

=0

Самостоятельно раскройте определитель и приведите получившееся уравнение к виду (24).

Это уравнение называетсяуравнением плоскости в отрезках.

Следствие. Любая плоскость определяется уравнением вида

Ax + By + Cz + D = 0 , (25)

которое называется общим уравнением плоскости. И обратно, всякое уравнение вида (25) определяет плоскость.

Упражнение. Доказательство этого следствия очень похоже на доказательство следствия 2 из §1. Докажите его самостоятельно.

Рассмотрим частные случаи плоскостей, задаваемых уравнениями вида (25).

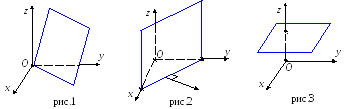
1. D = 0. Тогда уравнению Ax+By+Cz=0 удовлетворяют координаты точки O(0, 0, 0). Плоскость проходит через начало координат (рис.1).

2. C = 0. Имеем уравнение Ax + By +D = 0. Тогда вектор нормали к плоскости – n;\s\up8(( (A, B, 0) и n;\s\up8(( Oz, а значит,  Oz (рис.2).

Аналогично, при B=0 получим  Oy, а при A = 0 –  Ox.

3. A = B = 0. Имеем уравнение Cz+D=0, которое равносильно z = – C /D. Тогда Oz (рис.3).

Аналогично, при A = C = 0 будет  Oy, а при B = C = 0 –  Ox.

Теорема 6. Пусть плоскость  задаётся общим уравнением (25). Тогда расстояние от точки M(x₁, y₁, z₁) до плоскости вычисляется по формуле

h = . (26)

Эта теорема доказывается точно так же, как и теорема 4. Знак выражения зависит от того, в каком полупространстве относительно плоскости находится точка M.