ЭМММ лаба 1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение высшего профессионального образования «Кузбасский государственный технический университет»

Кафедра вычислительной техники и информационных технологий

ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Методические указания и задания для практических занятий

и самостоятельной работы студентов экономических специальностей по дисциплинам «Исследование операций в экономике» и «Экономико-математические методы и модели»

Составители М. А. Тынкевич Г. Н. Речко Е. В. Буйная

Утверждены на заседании кафедры Протокол № 3 от29.09.2010 Рекомендованы к печати учебно-методической комиссией по специальности 080801 Протокол № 2 от 29.09.2010

Электронная копия находится в библиотеке ГУ КузГТУ

КЕМЕРОВО 2010

1

Как известно, общая задача линейного программирования состоит в поиске значений переменных, удовлетворяющих некоторым линейным ограничениям и обеспечивающих наибольшее (наименьшее) значение заданной линейной функции. Например, требование:

максимизировать

L(x1, x2, x3) = 2x1 + x2 + 4x3

при условиях

x1 +2x2 + 3x3 ≤ 12, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0

означает пожелание не только отыскать значения неких величин x1, x2 и x3, удовлетворяющих вышеприведенным четырем условиям, но и среди них найти такие, что функция L(x1, x2, x3) принимает самое большое значение.

В роли неизвестных величин могут выступать, например, объемы выпуска продукции (обуви, приборов ночного видения или микроскопов), распределение денежных средств на ликвидацию ветхого жилья и строительство медицинских учреждений, тираж поэм М. Ю. Лермонтова и «заговоров от сглаза»; ограничения связаны с расходом материалов, наличием льгот на отдельные виды изданий, рыночной конъюнктурой или личными предпочтениями, а целевая функция L(Х) может определять прибыль от произведенной продукции или объем неосвоенных средств.

Количество неизвестных величин, фигурирующих в постановке задачи, называют ее размерностью. Набор их значений, удовлетворяющих условиям задачи, называют планом (примером может служить программа производства – набор значений показателей, удовлетворяющий ограничениям по сырьевым, социальным и прочим факторам).

Может обнаружиться, что задача неразрешима – не существует ни одного плана (ограничения противоречат друг другу). Может быть единственный план или много (множество) планов, среди которых надо найти наилучший (оптимальный), дающий максимум прибыли

2

(морального удовлетворения, степени очистки воды) или минимум затрат (жалоб населения, отходов при деревообработке и др.).

Размерность реальных задач, как правило, велика (от десятков до нескольких сотен). Здесь мы намерены на примере двумерных задач дать читателю наглядное, графическое представление о существе решаемых линейных программ (полагая, что всякий человек способен рисовать на плоском листе бумаги и воспринимать конструкции окружающего нас трехмерного пространства). Наличие такого представления может помочь и при обобщении выводов на задачи бóльшей размерности.

Естественно, что для решения задачи желательно сначала получить представление о множестве планов (допустимых решениях) и лишь затем из этого множества выбрать наилучший (с точки зрения поставленной цели).

Обратимся к знаниям, полученным еще в школьные годы. Из-

вестно, что уравнение α X + β Y = γ на плоскости			(X,Y) изображает
прямую линию (2x + 3y = 7,		y = 0 или x – 2y = 0)	и для ее построе-
ния достаточно	взять пару	подходящих точек.	Неравенства же
α X + β Y ≤ γ или	α X + β Y ≥ γ определяют полуплоскости, ограни-

ченные прямой α X + β Y = γ.

Поскольку система ограничений двумерной задачи линейного программирования определяет множество точек плоскости, лежащих или на прямых линиях, или в полуплоскостях, ограниченных такими линиями, то множество планов может быть представлено точкой, частью прямой линии, фигурой, напоминающей выпуклый многоугольник, но никак не эллипсом, полумесяцем или другим криволинейным

объектом.
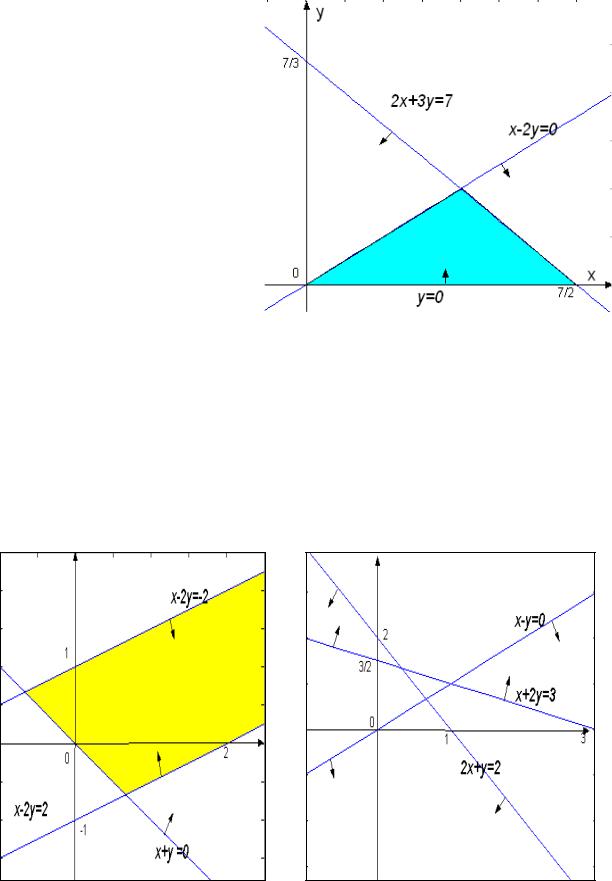
Так,	если ограничения	задачи описываются условиями
2x + 3y ≤ 7,	y ≥ 0, x – 2y ≥ 0,	первоначально строим соответствую-

щие прямые линии (прямую 2x + 3y = 7 по точкам пересечения с координатными осями; прямая y = 0 совпадает с осью 0x; прямая x – 2y = 0 проходит через начало координат и, например, точку с ко-

					3
	ординатами x = 2, y = 1).
	Выполнив столь «сложные»
	построения, выясняем, ка-
	кая же полуплоскость при-
	емлема	для соответствую-
	щего неравенства, для чего
	достаточно		взять	любую
	точку плоскости, не лежа-
	щую на прямой линии, и
	проверить		выполнение ог-
	раничения. Например, для
	проверки первого			ограни-
					Рис. 1
	чения	(соответствующая
	прямая	не	проходит через начало координат) можно взять точку
	(x = 0,	y = 0) и убедиться, что 2 0 + 3 0 < 7. Следовательно, эта точка

со всеми ее «соседями» до прямой линии (полуплоскость, её содержащая) соответствует неравенству 2x + 3y ≤ 7. На рис. 1 приемлемые полуплоскости выделены стрелками и общая их часть (множество точек, удовлетворяющих всем трем условиям; множество планов) пред-

Рис. 2

Рис. 3

4

ставлена выделенным здесь треугольником.

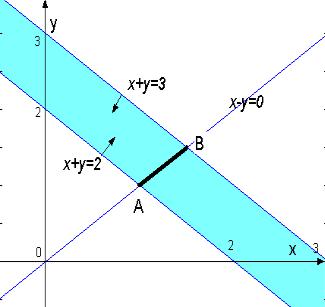
Возьмем систему ограничений вида -2 ≤ x + 2y ≤ 2, x + y ≥ 0. Построив соответствующие три прямых и выяснив подходящие полуплоскости, обнаруживаем, что множество планов – неограниченный многоугольник (треугольник, одну из вершин которого «отправили в бесконечность»), приведенный на рис. 2.

Если взять систему ограничений вида x + 2y ≥ 3, 2x + y ≤ 2, x − y ≥ 0, то легко убедиться (рис. 3), что ни одной точки, которая удовлетворяла бы всем трем условиям, найти не удастся – ограничения противоречивы (множество планов пусто).

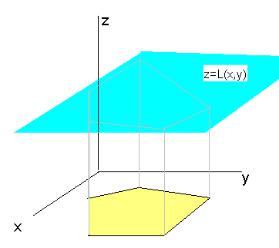
Возьмем систему ограничений, в которой наряду с неравенствами присутствуют равенства, например, 2≤ x + y ≤ 3, x − y = 0. Эта система требует, чтобы приемлемые решения (точки, планы) принадлежали полуплоскостям x + y ≥ 2, x + y ≤ 3 и лежали на прямой линии x − y = 0. Соответственно, здесь множество планов определяется отрезком АВ (координаты точек А и В можно найти из решения

	систем		{ x + y = 2, x −
	y = 0} и {x + y = 3, x − y
	= 0}	(рис. 4).
		Какие	же		выводы
	можно сделать из приве-
	денных примеров?
		Множество			планов
	двумерной		задачи		линей-
	ного	программирования
	представляет			собой		вы-
	пуклый		многоугольник
	(ограниченный			или		неог-
Рис. 4
	раниченный), отрезок пря-

мой линии (ограниченный или неограниченный), точку или отсутствовать по причине противоречивости ограничений (никаких криволинейных или невыпуклых фигур).

Рис. 5

5

Теперь, вспомнив о нашей цели, зададимся вопросом: какой же из найденного множества планов является оптимальным (обеспечивает наибольшее (наименьшее) значение нашей целевой функции)?

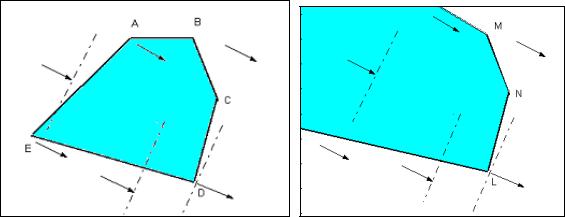
Нарисуем схематично не только множество планов в плоскости (x, y), но и целевую функцию z = L(x, y), изображаемую плоскостью трехмерного пространства, где значение z характеризует удаление этой плоскости от плоскости (x, y). Очевидно, что наибольшее и наименьшее удаление от множества планов имеет место в некоторых его вершинах,

но никак не в его внутренних точках (рис. 5).

Если подобное изображение не убеждает вас в этом (или вы забыли, что уравнение плоскости в трехмерном пространстве можно представить линейным уравнением α x + β y + γz = c), привлечем на помощь понятие о градиенте функции − векторе, составленном из ее частных производных, который показывает направление наибольшего возрастания функции в окрестности точки. Для нелинейных функ-

ций градиент меняется от точки к точке. Так, если f(x, y) = x2 + xy, то grad f(x) = {2x + y, x} в различных точках меняет свою ориентацию. В случае же линейной функции, составляющие ее градиента совпадают с ее коэффициентами, например grad{L(x, y) = 2x + 5y} = {2, 5}, и градиент остается неизменным во всех точках (в частности, во всех точках множества планов).

На рис. 6 мы изобразили множество планов задачи (многоугольник ABCDE) и показали стрелками направление градиента. Выбирая любую внутреннюю точку множества планов, мы видим, что в ее окрестности можно найти другую точку (смещением по градиенту в прямом или обратном направлении) c бóльшим (меньшим) значением

6

Рис. 6

Рис. 7

L(x ,y). Очевидно, что в данном случае максимум достигается в точке D, а минимум − в точке Е. Разумеется, если градиент перпендикулярен некоторой грани множества (отрезку прямой), то экстремум достигается во всех точках этого отрезка (в частности, и на его концах).

Напрашивается вывод, что при поиске точек экстремума (максимума или минимума) линейной функции (оптимальных планов)

достаточно рассматривать лишь вершины множества планов, но не внутренние его точки. Более того, в двумерном случае при достаточно аккуратных построениях с соблюдением масштаба можно не перебирать все вершины (количество их конечно, но может быть сравнительно большим), а сразу видеть экстремальную.

Обратите внимание на рис. 7, где множество планов является неограниченным. Построив градиент целевой функции, легко видеть, что максимум достигается в вершине L, тогда как по минимуму функция не ограничена (минимум L(x, y) → −∞). Этот пример сви-

детельствует, что в случае неограниченного множества планов может обнаружиться неограниченность L(x, y) по максимуму, мини-

муму или по обоим критериям.

Итак, графическое решение двухмерной линейной программы может привести к следующим исходам:

♦обнаруживается оптимальный план (может быть, и не один);

♦обнаруживается отсутствие оптимального плана (ограниче-

ния задачи противоречивы или целевая функция не ограничена за

7

счет неограниченности множества планов).

Если у вас остались какие-то сомнения, обратитесь к приведенным ниже примерам (здесь мы вместо принятых в школьной математике обозначений х и у используем символику х1 и х2; надеемся, что эта замена не приведет вас в смущение).

Пример 1. Решим задачу максимизации

L(x) = 2x1 + 3x2

при ограничениях	–x1	+ 2x2	≤ 6	(1)
	9x1 + 4x2 ≤ 56			(2)
	3x1	+ 5x2	≥ 4	(3)
	x1	≥ 0	≥ 0	(4)
		x2		(5)

Решение. Находим множество допустимых решений (планов) задачи, т.е. множество точек (x1, x2), удовлетворяющих заданной системе ограничений (1)−(5), для чего строим полуплоскости, соответствующие ограничениям задачи, и определяем их общую область.

Берем первое из условий и строим прямую линию –x1 + 2x2 = 6. Для этого находим любые две ее точки, например, точки пересечения с координатными осями: при x1 = 0 x2 = 3 и при x2 = 0 x1 = –6, то

есть точки (0, 3) и (–6, 0).	Чтобы выделить соответствующую полу-
	плоскость относительно построен-
	ной прямой, подставляем коорди-
	наты какой-либо другой точки (на-
	пример, начало координат) в ле-
	вую часть неравенства (1). Так при
	подстановке значений x1 = 0 и x2
	= 0 видим, что проверяемое усло-
	вие выполняется (0 ≤ 6). Следова-
	тельно, область допустимых реше-
	ний рассматриваемого неравенства
Рис. 8	–x1 + 2x2 ≤ 6 – та полуплоскость,
	которая включает начало коорди-

8

нат. Отображение второго ограничения абсолютно идентично.

Что касается полуплоскости третьего ограничения, то она располагается по отношению к граничной прямой по другую сторону, нежели начало координат.

Четвертое и пятое ограничения (x1 ≥ 0, x2 ≥ 0) соответствуют полуплоскостям, лежащим справа от оси ординат и над осью абсцисс

(первому квадранту плоскости).

В итоге получаем общую область для всех пяти полуплоскостей (множество планов) – выпуклый пятиугольник (рис. 8).

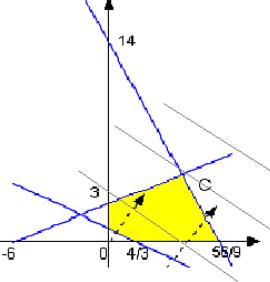
Теперь воспользуемся градиентом функции L(x) = 2x1 + 3x2. Здесь grad L(x) = (2, 3). Строим этот вектор на рисунке в отсчете от начала координат (или от любой точки плоскости, или от любой точки множества планов). Если точка экстремума не очевидна, возьмите «нить», перпендикулярную градиенту, и перемещайте над множеством планов в направлении градиента функции.

Обратите внимание на то, что во всех точках «нити» значение целевой функции одинаково (подобные «линии уровня» вы видите, например, на физических картах мира при изображении гор и глубин).

Нетрудно видеть, что точка последнего касания «нити» с множеством планов будет искомой точкой максимума функции L(x) (точка первого касания – точкой минимума). В нашем примере точкой максимума функции L(x) является точка С. Остается найти её координаты.

Поскольку она получается пересечением первой и второй прямых, то достаточно решить систему двух уравнений с двумя неизвестными

–x1 + 2x2 = 6 9x1 + 4x2 = 56.

Человек, знакомый с определителями и правилом Крамера, решает ее в виде:

9

6

2

−1

6

x =

56

4

= 6 4−2 56 =

−88

= 4; x

2

=

9

56

=

−1 56 −6 9

=

−110

= 5

.

−1 4−2 9

−22

−

−

−1 2

1

1

2

−

−

2

9

22

1 4

9

4

9

4

Если читатель не считается с затратами труда, он может решать

методом подстановок или любым другим приемом.

Итог труда: максимум целевой функции достигается в точке (4,

5) и равен

2x1 + 3x2 =

2 4 + 3 5 =

23.

Пример 2. Найдем экстремальные значения функции

L(x) = 3x1 – x2

при ограничениях

2x1 – 3x2 ≥ –6

(1)

x1 – 2x2

≤ 4

(2)

3x1 + 4x2

≥ 5

(3)

x1

≥ 0

(4)

Решение. Присутствующие

здесь

ограничения в

принципе

ничем не отличаются от ограни-

чений предыдущего примера, но

в итоге

построения

получается

множество планов в виде выпук-

лого

неограниченного

много-

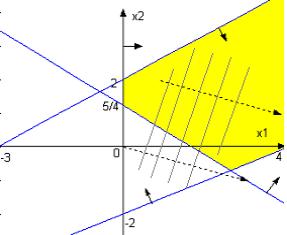
угольника (рис. 9). Если постро-

	Рис. 9	ить grad L(x) = (3, –1) и перпен-
		дикулярные ему «нити» (линии

уровня), легко видеть, что по максимуму L(x) не ограничена (L(Х)→ +∞), а минимум достигается в точке (0, 2) и равен L(0, 2) =– 2.

Пример 3. Найдем экстремальные значения функции
	L(x) = x1 – x2
при ограничениях	–x1 + 2x2	≤ 5	(1)
	x1 + x2	= 0	(2)
	x2	≥ 0	(3)

Решение. Строим область допустимых решений задачи (рис. 10). Поскольку второе ограничение представляет собой уравнение прямой