
- •1.Сходимость числового ряда
- •4. Признаки сравнения положительных рядов
- •Тогда ряд сходится или расходится одновременно с несобственным интегралом .
- •5. Знакочередующиеся ряды
- •6. Абсолютная и условная сходимость
- •7. Область сходимости функционального ряда
- •Теорема Абеля для степенных рядов
- •8. Радиус сходимости степенного ряда
- •Определение интервала сходимости
- •9. Почленное дифференцирование степенного ряда
- •Почленное интегрирование степенного ряда
- •10. Степенные ряды в окрестности произвольной точки.
- •11.Разложение элементарных функций в ряд Маклорена
- •15. Принцип умножения
- •16. Перестановки
- •Непосредственные следствия из аксиом
- •24. Схема равновозможных исходов
- •Алгоритм реализации схемы равновозможных исходов
- •Эмпирический закон больших чисел
- •25. Условная вероятность
- •26. Теорема умножения
- •27. Независимость событий
- •I. Независимость двух событий.
- •II. Независимость событий в совокупности.
- •30. Формула полной вероятности
6. Абсолютная и условная сходимость
 (1)
(1)
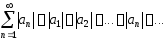 .
(2)
.
(2)
Определение. Если ряд (2), составленный из модулей, сходится, то ряд (1) называется абсолютно сходящимся.
Теорема. Если знакопеременный ряд (1) является абсолютно сходящимся, то он сходится (в обычном смысле).
Определение. Знакопеременный ряд (1) называется условно сходящимся, если он сходится, но не является абсолютно сходящимся, то есть если ряд (2), составленный из модулей его членов, расходится.
Условная сходимость ряда (1) связана в первую очередь не с тем, что его слагаемые быстро стремятся к нулю, а лишь с тем, что в частичных суммах слагаемые разных знаков в значительной мере взаимно погашают друг друга.
Теорема.Если ряд сходится условно, то за счет изменения порядка следования членов, можно обеспечить как сходимость ряда к любому наперед заданному значению суммы, так и расходимость ряда(cм., например, [3] ).
7. Область сходимости функционального ряда
Определение. Функциональным рядом называется выражение
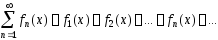 .
(1)
.
(1)
При
фиксированном
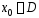 функциональному ряду (1) соответствует
числовой ряд
функциональному ряду (1) соответствует
числовой ряд
 .
(2)
.
(2)
При
одних значениях
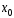 этот числовой ряд может сходиться, при
других — расходиться.
этот числовой ряд может сходиться, при
других — расходиться.
Определение.
Совокупность
 всех тех значений
всех тех значений ,
при которых числовой ряд (2) сходится,
называетсяобластью
сходимости функционального ряда
(1).
,
при которых числовой ряд (2) сходится,
называетсяобластью
сходимости функционального ряда
(1).
При
 определена функция
определена функция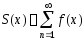 — сумма числового ряда (2) в точке
— сумма числового ряда (2) в точке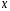 .
.
Теорема Абеля для степенных рядов
Определение.
Степенным
рядом в окрестности точки
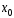 называется функциональный ряд вида
называется функциональный ряд вида
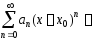
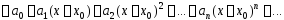 .
(3)
.
(3)
Ряд
(3) называют также рядом
по степеням
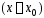 .
Числа
.
Числа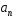 называютсякоэффициентами
степенного ряда.
называютсякоэффициентами
степенного ряда.
Теорема
Абеля. 1. Если
степенной ряд

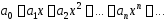 (4) сходится
в точке
(4) сходится
в точке
 ,
то онабсолютно
сходится при всех
,
то онабсолютно
сходится при всех
 ,
удовлетворяющих условию
,
удовлетворяющих условию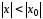 ,
то есть при
,
то есть при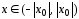 .
.
2.
Если степенной ряд (4)
расходится в точке
 ,
то он расходится при всех
,
то он расходится при всех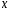 ,
удовлетворяющих условию
,
удовлетворяющих условию .
.
8. Радиус сходимости степенного ряда
Определение.
1. Если
областью сходимости степенного ряда
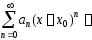
 является
конечный промежуток, то интервалом
сходимости
степенного ряда называется интервал
является
конечный промежуток, то интервалом
сходимости
степенного ряда называется интервал
 такой, что в точках
такой, что в точках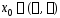 ряд сходится абсолютно, а в точках
ряд сходится абсолютно, а в точках ряд расходится. Число
ряд расходится. Число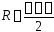 называется при этомрадиусом
сходимости
степенного ряда.
называется при этомрадиусом
сходимости
степенного ряда.
2.
Если областью
сходимости является вся числовая ось
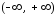 ,
то полагают
,
то полагают .
.
3.
Если область сходимости состоит только
из нулевой точки, то полагают
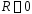 .
.
В
граничных точках интервала сходимости
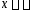 и
и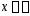 ряд может как сходиться, так и расходиться.
ряд может как сходиться, так и расходиться.
Определение интервала сходимости
Пусть
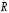 радиус сходимости степенного ряда
радиус сходимости степенного ряда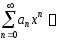
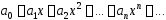 Поскольку при
Поскольку при ряд сходится абсолютно, рассмотрим ряд,
составленный из модулей:
ряд сходится абсолютно, рассмотрим ряд,
составленный из модулей:
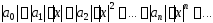 ,
(1)
,
(1)
и
применим к нему признак Даламбера. Пусть
существует предел
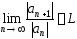 .
.
1.
Пусть сначала
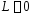 — конечное число; тогда при
— конечное число; тогда при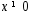 :
:
 .
.
По
признаку Даламбера положительный ряд
(1) сходится, если
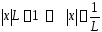 ,
и расходится, если
,
и расходится, если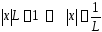 .
Поэтому для радиуса сходимости
.
Поэтому для радиуса сходимости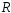 степенного ряда
степенного ряда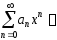
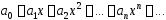 справедлива формула:
справедлива формула:
 .
(2)
.
(2)
2.
Если
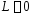 ,
то неравенство
,
то неравенство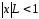 выполняется при всех
выполняется при всех
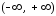 ,
так что в этом случае
,
так что в этом случае .
.
3.
Если
 ,
то ряд расходится при всех
,
то ряд расходится при всех ,
и
,
и .
.
9. Почленное дифференцирование степенного ряда
Теорема. Пусть степенной ряд
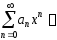
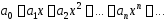
имеет
радиус сходимости
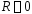 ,
и
,
и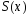 при
при — его сумма. Тогда функция
— его сумма. Тогда функция дифференцируема в интервале
дифференцируема в интервале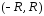 ,
степенной ряд
,
степенной ряд
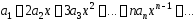 ,
,
составленный
из производных членов исходного ряда,
имеет тот же интервал сходимости, и его
сумма равна
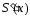 :
:
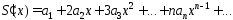 . (1)
. (1)
