На сортировку / 3 / Sabak / ИжКГ тема / Лекция ИжКГ
.docx
|
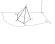
1.Пішінніњ белгілі бір ереже бойынша жазыќтыќќа (бетке) тусірілген кескіні проекция деп аталады. Нєрсе кескінін алу ушін жасалатын єрекетті проекциялау дейді.Нуктеніњ проекциясын турѓызу ушін сол нукте арќылы µтетін проекциялаушы сєуленіњ проекциялар жазыќтыѓымен ќиылысу нуктесін табу ќажет (1.1 сурет): [SA) ∩ 1=A1.
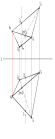
S – проекция центрі;А –кењістіктегі нукте; SA – проекциялаушы сєуле;1-проекциялар жазыќтыѓы;А1- А нуктесініњ 1-дегі проекциясы. S нуктесі шекті қашыќтықта жатса, онда ол меншікті, ал шексіз ќашыќтыќта жатса меншіксіз деп аталатыны белгілі.Егер S нуктесі меншікті нукте болса, онда проекциялау центрлік проекциялау (1.1 - сурет), Проекциялаудыњ негізгі ќасиеттері Проекциялаудың кез келген түріне тән екі ќасиет бар:-нүктенің проекциясы нүкте болады; -түзудің проекциясы жалпы жағдайда түзу болады.SA жєне SB түзулері жазыќтыќты ќұрайды, ал жазыќтыќтардың ќиылысу сызығы әрқашанда - түзу (1.1 - сурет). Центрлік проекциялар заттарды көрнекті етіп кескіндегенімен, олардың нақты қалпыларын және өлшемдерін айтарлықтай бұрмалайды;центрлік проекциялау негізінен сәулет өнері мен құрылыс сызбаларында қолданылады 2.Параллель проекциялау. Параллель проекциялаудың қасиеттері.Егер меншіксіз болса, онда ол параллель проекциялау деп аталады (1.2 - сурет).Параллель проекциялауѓа тєн ќасиеттер:-тузудіњ бойынан алынѓан нуктеніњ проекциясы сол тузу проекциясыныњ бойында жатады (1.1 – суретте D н‰ктесі);-егер екі тузу кењістікте озара параллель болса, онда олардыњ проекциялары да µзара параллель болады (1.3 - сурет):αжєне жазыќтыќтары озара параллель, сондыќтан А1В1 С1D1;
-егер н‰кте кењістіктегі кесіндіні белгілі бір ќатынаста бµлетін болса, онда н‰ктеніњ проекциясы кесіндініњ проекциясын да сондай ќатынаста бµледі (1.4 - сурет):СС1ВВ1, сондықтан АВВ1АСС1.Ал егер ұшбұрыштар конгурентті болса, онда АС = А1С1 СВ С1В1 .Паралель проекциялар пішіндердің кейбір қасиеттерін сақтай отырып, олардың нақты қалыптарын және өлшемдерін едәуір кем бұрмалайды. Алайда, параллель проекциялау тәсілі кішігірім өлшемді объектілерді кескіндеуде аса қолайлы
11.Дербес жағдайдағы жазықтықтар:Дербес жағдайдағы жазықтықтар екіге бөлінеді:а) бір проекция жазықтығына параллель жазықтықтар деңгейлік жазықтықтар деп аталады:- 1-ге параллель жазықтық горизонталь жазықтық деп аталад. Горизонталь жазықтық проекцияларының ереекшеліктері (1.19 - сурет):
1.19-сурет
1.20-сурет 1)фронталь проекциясы х осіне параллель түзу 2 х 2)бұл жазықтықта жатқан кесінділер 1-ге өздерінің нақты шамаларымен проекцияланады: А1В1С1= ABC Көбіне дербес жағдайдағы жазықтықтар бір ғана проекциясымен беріледі (1.20 - сурет). Бұл проекциясының жинаушылық қасиеті бар, яғни осы жазықтықтың бойында жататын кез келген пішін бір түзудің бойына проекцияланады.- 2-гепараллельжазықтықфронтальжазықтықдепаталады.Проекцияларерекшеліктері (1.21 - сурет):1) 1х: 2) m2 n2= m n; 3) 1 жинаушылық қасиетін иеленеді.
-
3-ке
параллель жазықтық профиль деп
аталады.ә) тек бір ғана проекция
жазықтығына перпендикуляр жазықтықтар
проекциялаушы жазықтықтар деп
аталады:- 1-ге
перпендикуляр жазықтық горизонталь
проекциялаушы жазықтық деп аталады,
1.Проекциялар
ерекшеліктері (1.22 - сурет)1) 1
жинаушылық қасиетін иеленеді:2) (
^ 2)
= (1
^ х ) - 2-ге
перпендикуляр жазықтық фронталь
проекциялаушы жазықтық, 2.Проекциялар
ерекшеліктері (1.23 - сурет): 1) 2
жинаушылық қасиетін иеленеді:2)
(
^ 1)=(2
^ x)- 3-ке
перпендикуляр жазықтық профиль
проекциялаушы жазықтық.
1.23-сурет. Жазықтыққа перпендикуляр түзу Түзу жазықтыққа перпендикуляр болу үшін ол осы жазықтықтың өз қиылысқан екі түзуіне перпендикуляр болуы қажет. Ол үшін комплекс сызбада түзудің горизонталь проекциясы жазықтық горизонталінің горизонталь проекциясына, ал фронталь проекциясы жазықтық фронталінің фронталь проекциясына перпендикуляр болуы қажет және жеткілікті.
Мысалы (1.36 – сурет): Б. (АВС), D Т. к. n, {nD, n}ЕША 1) h (ABC) 2) n1 D1, n1 h1 3) f (ABC) 4) n2D2, n2 f2 Өзара перпендикуляр жазық тықтар:Жазықтықтар өзара перпендикуляр, егер олардың бірі екінші жазықтыққа перпендикуляр түзу арқылы өтсе. Мысалы (1.37 - сурет): Б. (mn), DE Т. к. , {DE, }ЕША:1) h 2) L1h1, L1 D1 3) f 4) f2 L2, L2 D2 5)(L DE) , (L DE)
9..Нуктеніњ
ортогональ проекциясын турѓызу ушін
сол нукте арќылы проекциялар жазыќтыѓына
тусірілген перпендикулярдыњ табанын
тапса жеткілікті. (1.5 - сурет). Тік
бұрышты прекциялау әдісі паралель
проекциялау әдісінің дербес бір түрі
болып табылады: проекциялаушы сәулелер
проекциялар жазықтығына 1.5 перпендикуляр болады
13 Түзу мен жазықтықтың параллельдігі
Егер
жазықтықтан тысқары алынған түзу осы
жазықтықта жатқан түзулердің біріне
параллель болса, онда ол түзу жазықтыққа
параллель болады (1.30- сурет Б. (mn), L2 , А {L (mn)} Т. к. L1 ЕША 1) t2 L2 ,t ; 2) ↕ t1 3) L1A1^ L1 t1
Жазықтыққа
перпендикуляр түзу
Түзу жазықтыққа перпендикуляр болу
үшін ол осы жазықтықтың
өзара қиылысқан екі түзуіне
перпендикуляр
болуы қажет. Ол үшін комплекс
сызбада түзудің горизонталь проекциясы
жазықтық горизонталінің горизонталь
проекциясына, ал фронталь проекциясы
жазықтық фронталінің фронталь
проекциясына перпендикуляр болуы
қажет және жеткілікті. Мысалы (1.36 –
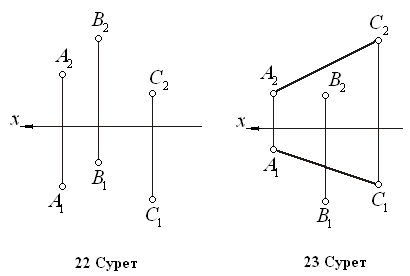
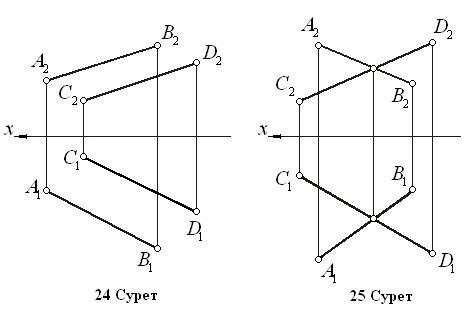
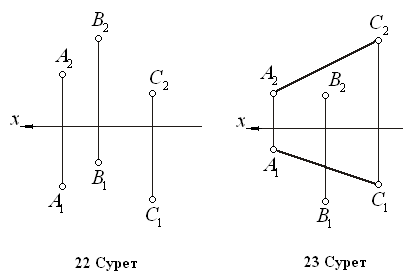
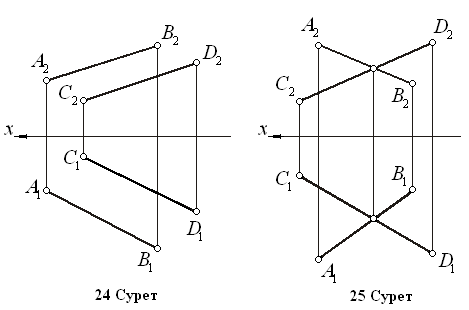
сурет): Б. (АВС), D Т. к. n, {nD, n} ЕША 1) h (ABC) 2) n1 D1, n1 h1 3) f (ABC) 4) n2D2, n2 f2 4.1 Жазықтықтың сызбасы Жазықтықтар алты түрлі әдіспен берілуі мүмкін. 1.Бір түзудің бойында жатпайтын 3 нүкте арқылы (22 Сурет). 2.Түзу және оның бойында жатпайтын нүкте арқылы (23 Сурет) 3.Екі өзара параллель түзу арқылы (24 Сурет). 4.Екі өзара қиылысқан түзулер арқылы (25 Сурет).
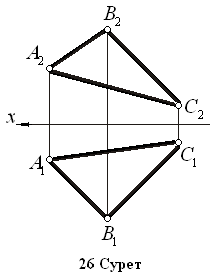
5.Кез
– келген жазық фигура арқылы (26 Сурет).
6.Жазықты
қтар өзінің іздерімен берілуі мүмкін. Іздері деп жазықтықтың проекциялар жазықтықтарымен қиылысқан сызықтарын айтады (27 Сурет). Суретте һ0- жазықтықтың горизонталь ізі, f0- фронталь ізі, p0- профиль ізі. 16. БеттерЖалпы түсініктер Жасаушы деп аталатын сызықтың бағыттаушы деп аталатын сызықтың бойымен үздіксіз қозғалғандағы орындарының жиыны бет деп аталады (1.38 - сурет): m- бағыттаушы сызық;l- жасаушы; Ф- бет.Сызбада беттерді көрсету үшін 2 түрлі әдіс қолданылады: қаңқа арқылы және кинематикалық. Кинематикалық әдіс қолданғанда бет өзінің анықтаушысымен беріледі. Анықтаушы деп бетті бір мәнді анықтайтын бір-біріне тәуелсіз шарттар жиынтығын атайды. Жалпы жағдайда бет
берілді
деп есептеледі, егер
1.38 - сурет Кез келген нүктесінің
бетке тиісті немесе
тиісті еместігін анықтай алсақ.Беттердің жіктемесі
а)
барлық беттер жасаушылары тұрақты
немесе тұрақсыз беттер деп екіге
бөлінеді;ә) Жасаушылары түзу сызық
болатын беттер түзу сызықты қисық
беттер деп аталады;б) түзу сызықты
қисық беттердің өзі екіге бөлінеді:
жазылатын немесе жазылмайтын бет
Конустық
бет:
Конустық бет түзу жасаушы L-дың қисық
бағыттаушы m –ның бойымен қозғалысынан
пайда болады. Бұл жерде жасаушының
бір нүктесі әр уақытта қозғалмайды,
ол конустық беттің төбесі – S нүктесі
(1.42 -с).Беттегі
нүкте:Нүкте
беттің бойында жатады, егер ол осы
беттің кез келген сызығының бойында
жатса. Мысалы
(1.483-с): Б. ,
А2, В1{A ,
B }Т.
к. А1 ,В2 ЕШАІ. 1) а2А2,
а2
х 2) ↨ а13) ↨ А1 , {A
a}.ІІ. 1) S1B1=
T1 2) ↕ S2, T2 3) ↕ B2, B2S2,
T2.
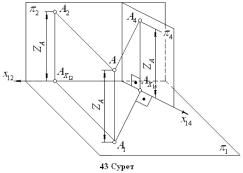
21.Параллель аксонометриялық проекциялардың жасалуыАксонометриялық проекциялардың Монж әдісінен негізгі айырмашылығы
–проекция
жазықтығы тек қана Біреу,болады.Сондықтан, кескін қайтымды болуы үшін, оны берілген фигурамен байланыстырылған тік бұрышты координаталар өстерімен толықтырадыСонымен, аксонометриялық проекция – денені координаталар өстерімен
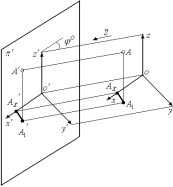
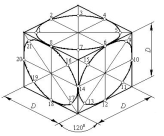
байланыстыра отырып, өзара параллель проекциялаушы сәулелердің көмегімен тек бір ғана жазықтыққа түсіргенде пайда болады. Суретте: π’ - аксонометрияның проекциялар жазықтығы;S - проекциялау бағыты; x’, y’, z’аксонометриялық өстер;OAxAA1 - координаталар сынық сызығы; O’Ax’A1’A’ - координаталар сынық сызығының аксонометриялық проекциясы. Координаталар сынық сызығының әрбір кесіндісі (буыны)A - нүктесінің тік бұрышты координаталарының,бірін анықтайды. Мәселен,OAx=XA,AxA1=YA,A1A=ZСонда m=O’A’x/OAx, n=Ax’A’1/AxA1 және K=A1’A’/A1A - қатынастарды аксонометриялық x’, y’, z’осьтер бойынша бұрмалану коэффициенттері деп атайды.2 Параллель аксонометрияның негізгі теоремасы Координаталар жүйесі(OXYZ) және аксонометриялық проекциялар жазықтығының (π’) өзара орналасуына және проекциялау бағытына байланысты сан алуан аксонометриялық проекциялар алуға болады. Олар бір бірінен аксонометриялық осьтердің бағытымен және бұрмалану
коэффициенттерінің
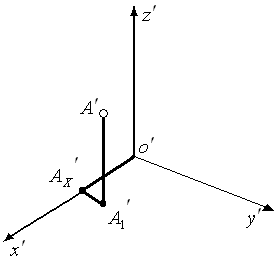
мәнімен айырылады. Осы айтылғанның дұрыстығын кезінде неміс ғалымы Карл Польке көрсеткен. Ол мынадай теореманы дәлелдеді: бір жазықтықта жатқан, бір нүктеден өзара кез келге бұрыш жасай шығып тұрған, ұзындығы кез – келген шамаға тең үш кесінді тік бұрышты координаталар осьтерінде жатқан координаталар системасының бас нүктесінен салынған өзара тең үш кесіндінің параллельдік проекциялары болып табылады.Бұл теореманы параллель аксонометрияның негізгі теоремасы деп атайды.Бұрмалану коэффициенттерін және осьтер арасындағы бұрыштарды тағайындап кез – келген геометриялық фигураның аксонометриялық проекциясын , оған тиісті нүктелер проекциялары арқылы тұрғызуға болады.Есеп A нүктесінің координаталары A(XA,YA,ZA), аксонометриялық осьтердің (x’, y’, z’) бағыттары және бұрмалану коэффициенттері (m,n,k) берілген.A нүктесінің аксонометриялық проекциясын (A’) тұрғызу керек.Шығару жолы.Біріншіден, аксонометриялық осьтерін(x’, y’, z’) берілген бағыттары бойынша саламыз (2 Сурет).Екіншіден, аксонометриялық осьтерде бұрмалану коэффициенттерді ескеріп, нүктенің аксонометриялық координаталарын табамыз.O’Ax’=XA*m: Ax’A1’=YA*n: A1’A’=ZA*k Сонан соң, A нүктесінің аксонометриялық проекциясын (A’) тұрғызамыз. Параллель аксонометриялық проекциялардың түрлеріь Проекциялау бағытына байланысты аксонометрия екі түрге бөлінеді.
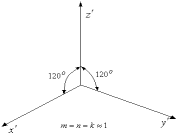
Бұрмалану коэффициенттерінің мәніне байланысты үш түрге бөлінеді:1.Изометриялық, егер m=n=k;2.Диметриялық, егер m=n≠k, немесе m=k≠n , немесе n=k≠m;1)Триметриялық, егер.m≠n≠k МЕСТ 2.317 – 69 мемлекеттік стандарт өнеркәсіп пен құрылыстың барлық салаларында пайдаланылатын сызбаларда аксонометрияның бес түрін қолдануға ұсыныс жасайды:1.Тік бұрышты изометрия және диметрия.2.Қиғаш бұрышты фронтальдық және горизонтальдық изометрия.3.Қиғаш бұрышты фронтальдық диметрия.Аксонометрияның бұл түрлерін стандарттық проекциялар
дейді.
5 Стандарттық аксонометриялық проекциялар осьтері арасындағы бұрыштарТік бұрышты аксонометриялық проекцияда <ᵩ0=900, сондықтан жоғарыдағы теңдеу былай жазылады m2+n2+k2=2 Изометрияда m=n=k, сондықтан
олардың
әрқайсысы
ал осьтер арасындағы бұрыштар өзара тең, яғни 3600:3=1200 болады.
22.Параллель аксонометриялық проекциялардың жасалуыАксонометриялық проекциялардың Монж әдісінен негізгі айырмашылығы
–проекция
жазықтығы тек қана Біреу,болады.Сондықтан, кескін қайтымды болуы үшін, оны берілген фигурамен байланыстырылған тік бұрышты координаталар өстерімен толықтырадыСонымен, аксонометриялық проекция – денені координаталар өстерімен
байланыстыра отырып, өзара параллель проекциялаушы сәулелердің көмегімен тек бір ғана жазықтыққа түсіргенде пайда болады. Суретте: π’ - аксонометрияның проекциялар жазықтығы;S - проекциялау бағыты; x’, y’, z’аксонометриялық өстер;OAxAA1 - координаталар сынық сызығы; O’Ax’A1’A’ - координаталар сынық сызығының аксонометриялық проекциясы. Координаталар сынық сызығының әрбір кесіндісі (буыны)A - нүктесінің тік бұрышты координаталарының,бірін анықтайды. Мәселен,OAx=XA,AxA1=YA,A1A=ZСонда m=O’A’x/OAx, n=Ax’A’1/AxA1 және K=A1’A’/A1A - қатынастарды аксонометриялық x’, y’, z’осьтер бойынша бұрмалану коэффициенттері деп атайды.Бұрмалану коэффициенттері мен проекция бағыты арасындағы байланыс:Проекциялаушы сәулелер мен аксонометрия жазықтығының арасындағы бұрышты φ0 деп
белгілейді.
Сонда, бұрмалану коэффициенттері мен φ0 бұрышы мынадай теңдеу арқылы байланысады: m2+n2+k2=2+ctg2φБұл аксонометрияның негізгі формуласы болады. Теңдеуді шығару жолын сызба геометрия оқулықтарынан табуға болады.Диметрияда көбінесе
m=k,
ал n– ді олардың жартысына тең алады.
Сондықтан
жоғарыдағы теңдеуге сүйене отырып,
олардың мәндерін табуға болады m=k=
|
3.Нуктеніњ
ортогональ проекциясын турѓызу ушін
сол нукте арќылы проекциялар жазыќтыѓына
тусірілген перпендикулярдыњ табанын
тапса жеткілікті. (1.5 - сурет). Тік
бұрышты прекциялау әдісі паралель
проекциялау әдісінің дербес бір түрі
болып табылады: проекциялаушы сәулелер
проекциялар жазықтығына перпендикуляр
болады .Екi
озара перпендикуляр азыктыктарга
проекциялау:Нуктенин
кенистикте орналаскан жерiн аныктау
ушiн,онын кемiнде екi проекциясы белгiлi
болуы керек.Ортогональ проекциялау
адiсiнде булл проекциялар екi озара
перпендикуляр , 1
ж/е2
жазыктыктарда
болады.(1.6сурет)
4..Нуктеніњ ортогональ проекциясын турѓызу ушін сол нукте арќылы проекциялар жазыќтыѓына тусірілген перпендикулярдыњ табанын тапса жеткілікті. (1.5 - сурет). Тік бұрышты прекциялау әдісі паралель проекциялау әдісінің дербес бір түрі болып табылады: проекциялаушы сәулелер проекциялар жазықтығына перпендикуляр болады 1.5сурет.Кейде объектінің екі проекциясы оның қалпы мен өлшемдері туралы керекті мәліметтерді білуге жеткілікті бола алмайды, сондықтан 1.7- суретте көрсетілген 1-мен 2 жазықтықтар жүйесіне қосымша оның екеуіне де перпендикуляр 3 жазықтығын енгізейік. Сонда (1.9- сурет) проекциялар жазықтықтарының қиылысу сызықтары- проекциялар осьтері үшеу болады: х- абцисса, у- ордината, z- аппликата.
1.5
Осьтердің тоғысу нүктесі (0) координаталар басы деп аталады. А нүктесінің төмендегідей координаталары болады:А (ХА; YА; ZА) , суретте Х=3, Y = 4, Z= 6, сондықтан А(3;4;6).А3 профиль проекциялар жазықтығы 3 – те пайда болған А нүктесінің профиль проекциясы деп аталады. Нүктенің фронталь және профиль проекциялары z осіне перпендикуляр түзудің бойында жататынына назар аударыңыздар (1.10- сурет).Нүктенің профиль проекциясының оның горизонталь проекциясымен қалай байланысқаны 1.10- суретте анық көрсетілген. k0 – ді комплекс сызбаның тұрақты түзуі дейді.
5.Нуктеніњ
ортогональ проекциясын турѓызу ушін
сол нукте арќылы проекциялар жазыќтыѓына
тусірілген перпендикулярдыњ табанын
тапса жеткілікті. (1.5 - сурет). Тік
бұрышты прекциялау әдісі паралель
проекциялау әдісінің дербес бір түрі
болып табылады: проекциялаушы сәулелер
проекциялар жазықтығына перпендикуляр
болады. Жазықтықтың сызбасы Жазықтықтар алты түрлі әдіспен берілуі мүмкін.(1.5 –сурет) 1.Бір түзудің бойында жатпайтын 3 нүкте арқылы (22 Сурет). 2.Түзу және оның бойында жатпайтын нүкте арқылы (23 Сурет) 3.Екі өзара параллель түзу арқылы (24 Сурет).4.Екі өзара қиылысқан түзулер арқылы (25 Сурет). 5.Кез – келген жазық фигура арқылы (26 Сурет).
6.Жа
зықтықтар өзінің іздерімен берілуі мүмкін. Іздері деп жазықтықтың проекциялар жазықтықтарымен қиылысқан сызықтарын айтады (27 Сурет). Суретте һ0-жазықтықтың горизонталь ізі, f0- фронталь ізі, p0- профиль ізі.2 есеп: Жазықтықтың ерекше түзулеріЖазықтықтың ерекше түзулері деп, осы жазықтықтың бойында жататын және проекциялар жазықтарының біріне параллель түзулерді атайды. 1.29- суретте жазықтың екі ерекше түзуі – горизонталь мен фронталь көрсетілген.
а)
жазықтықтың горизонталі h1?; h (ABC)
ә) жазықтың фронталі f2
1.29 - сурет
19.Айналу беттері Түзу немесе қисық сызықты жасаушылар - дың тұрақты осьтері төңірегінде айналуынан пайда болған қисық беттерді айналу беттері деп атайды. Айналу кезінде жасаушының әрбір нүктесі айналу осі арқылы шеңбер сыза қозғалады және бұл шеңбердің жазықтығы айналу осіне перпендикуляр орналасады.Айналу беттері техникада өте көп тараған. Мысалы, конустық және цилиндрлік айналу беттері, сфера , тор, айналу эллипсоиды, айналу параболоиды, т. с. с.
Жақты
беттің жазықтықпен қиылысуы.Беттің
жақтары жазықтықтардың бөліктері
болғандықтан, олар қиюшы жазықтықпен
түзулер арқылы қиылысады. Бұл жағдайда
қиылысу сызығы тұйық немесе тұйық
емес сынық сызық болады. Қиылысу сызығын тұрғызу үшін беттің қырларының қиюшы жазықтықпен қиылысу нүктелерін тауып , оларды өзара көріну не көрінбеуін ескеріп қосса жеткілікті.Мысалы (1.44 - сурет) : SA= 1 (12, 11); SB= 2 (22, 21); SC= 3 (32, 31); (SABC)= 123 Сфераның жазықтықпен қиылысуы :Бұл жағдайда қиылысу сызығы шеңбер болады:а) қиюшы жазықтық деңгей жазықтығы (1.45а- сурет);ә) қиюшы жазықтық проекциялаушы жазықтық (1.45ә- сурет).
Айналу цилиндр бетінің жазықтықпен қиылысуы Бұл жағдайда мынадай қиылысу сызықтары пайда болуы мүмкін (1.46.- сурет):а) шеңбер, егер қиюшы жазықтық і- ге перпендикуляр болса;ә) эллипс, егер қиюшы жазықтық беттің барлық жасаушыларын қиса, немесе і- ге перпендикуляр немесе параллель болмаса;б) екі жасаушы ( түзулер ), егер қиюшы жазықтық і –ге параллель болса.
20.Айналу беттері Түзу немесе қисық сызықты жасаушылар - дың тұрақты осьтері төңірегінде айналуынан пайда болған қисық беттерді айналу беттері деп атайды. Айналу кезінде жасаушының әрбір нүктесі айналу осі арқылы шеңбер сыза қозғалады және бұл шеңбердің жазықтығы айналу осіне перпендикуляр орналасады.Айналу беттері техникада өте көп тараған. Мысалы,
конустық 12. Проекцияларды түрлендіру тәсілдері Көп жағдайларда геометриялық есептерді шығару үшін проекцияларды түрлендіріп, денелерді бізге ыңғайландырып дербес жағдайға келтіру керек болады.Бұл есептерді шығарудың екі жолы бар:а) проекция жазықтықтарын алмастыру тәсілі; б) бұру тәсілі.Проекциялар жазықтықтарын алмастыру тәсілін кейбір метрлік есептерді шығаруда қолданылады. Нүктеден жазықтыққа дейінгі қашықтықты табу: Шығарудың жалпы схемасы:Проекциялар жазықтықтарын алмастыру тәсілін қолданып, эпюрде берілген жалпы жағдайдағы жазықтықты дербес (проекциялаушы) жағдайға келтіреміз. Ол үшін осы жазықтықтың горизонталін жүргізіп π 4 –ті соған перпендикуляр етіп жүргіземіз.Мысалы (1.55 - сурет): Б. (АВС), D Т.к. [D ∙ α (АВС)
ЕША
14.Проекциялар
жазықтарын алмастыру тәсілі
Тәсілдің мәнісі:Бұл тәсіл бойынша,
кеңістікте берілген обьектіні өзгертпей
қалдырады да, проекциялар жазықтықтарының
кез келгенін бізге қолайлы болып
табылатын басқа жазықтықтармен
алмастырып, обьекті проекцияларын
қайта тұрғызады. Жаңадан алған
проекциялар жазықтығы ескі (алмастырылған)
проекциялар жазықтығына перпендикуляр
болып алынады (1.54 - сурет). π2-ні
π 4-ке
алмастырамыз. А нүктесінен π4-ке
перпендикуляр түсіріп, А4
нүктесін табамыз: π 4 – жаңа проекциялар жазықтығы;π 2 - алмастырылатын (ескі) проекциялар жазықтығы;π 1 – алмастырылмайтын проекциялар жазықығы.А4 Ах14 = АА1 = А2Ах Қорытындылар: а) нүктенің жаңа проекциясы (А4) және ескі алмастырылмайтын проекциясы (А1) жаңа проекция осіне (Х14) перпендикуляр бір түзудің бойында жатадыА4А1 Х14; ә) нүктенің жаңа проекциясынан (А4 ) жаңа осіне (Х14) дейінгі қашықтық (А4 Ах14), сол нүктенің ескі алмастырылатын проекциясынан (А2) ескі осіне (Х12) дейінгі қашықтыққа тең А4 Ах14= А2 Ах12 Екі нүктенің ара қашықтығын табу Мысалы (1.54 - сурет):Б. А,В Т.к. [АВ] ЕША1) π 2 → π 4 → Х14 ││А1В1 А4В4=[АВ] Жазық пішінінің ауданының нақты шамасын табуШығарудың жалпы схемасы:Проекциялар жазықтықтарын алмастыру тәсілін қолданып, берілген жазықтықты проекциялар жазықтығына параллель жағдайға келтіреміз.Мысалы: (1.57 - сурет)Б. α (АВС)
Т.к.
[АВС] ЕША 3) 3)A4, B4, C4 4) 5(ABC)x45A4B4C4 5) 5) (A5B5C5)= [ABC] 15.Айналдыру тәсілі:
Бұл
тәсіл бойынша белгілі бір осьтен
айналдыру арқылы кеңістіктің
геометриялық модельдерінің орындары
өзгертіліп, берілген проекциялар
жазықтықтарының жүйесінде дербес
жағдайға келтіріледі. Кез келген нүкте
осьтен айналғанда шеңбер сызатыны
және бұл шеңбер жазықтығы осы оське
перпендикуляр екені белгілі.Сондықтан,
айналу осьтері ретінде проекциялаушы
немесе деңгейлік түзулерді қабылдасақ,
онда нүктелердің айналу жазықтықтары
проекция жазықтықтарына параллель
немесе перпендикуляр болады. Мысалы
(1.60 - сурет ):Горизонталь проекциялаушы
түзу (і) төңірегінде айналдырған кезде
А нүктесінің горизонталь проекциясы
А1
шеңбер бойымен қозғалады, ал фронталь
проекциясы А2-
осьтің фронталь проекциясына
перпендикуляр түзудің бойымен
қозғалады.Айналдыру тәсілімен
кесіндінің нақты шамасын табу үшін
(1.61-.сурет), айналу осін (і) кесіндінің
шеткінүктелерінің
бірі арқылы өтетін қылып алу қажет.
Сонда айналдырғандаА2О2А2В2х
В1А1
=
AB.Сонымен
қатар түзудің көлбеулік бұрышы да
табылады АВ
2.Жазық
пішінінің ауданының нақты шамасын
табу.
Шығарудың жалпы схемасы: Проекциялар жазықтықтарын алмастыру тәсілін қолданып, берілген жазықтықты проекциялар жазықтығына параллель жағдайға келтіреміз.
Мысалы:
(1.57 - сурет) Б. α (АВС) Т.к. [АВС] ЕША 1)h 2) 4hx14 h1 3) A4, B4, C44) 5(ABC)x45A4B4C45) (A5B5C5)= [ABC]
|
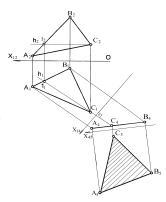
6. Түзудің іздері. Келесіні анықтауға мысал келтіріңіз. Түзумен проекция жазықтықтарының қиылысқан нүктелері түзудің іздері деп аталады (18 Сурет).
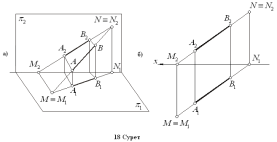
Горизонталь ізінің горизонталь проекциясы (М1-нүктесі) ізінің өзімен беттеседі, ал фронтальпроекциясы (М2) Х- oсінде жатады. Фронталь ізінің фронталь проекциясы (N2)өзінің ізімен беттеседі, ал горизонталь проекциясы (N1)x - осінде жатады.Сонымен, ABтүзуінің горизонталь ізін табу үшін, оның фронталь (A2B2) проекциясын X- осіне дейін созып, M2 нүктесінен оське перпендикуляр тұрғызу керек. Сол перпендикулярдың A1B1проекциясының жалғасымен қиылыстырып, M≡M1- горизонталь ізін табамыз. Сондай әдіспен N≡N1 фронталь ізін табамыз.Егер түзу проекция жазықтықтарының біріне параллель жатса, онда сол жазықтықта түзудің ізі болмайды, өйткені түзу ол жазықтықпен қиылыспайды. 8.Екі түзудің өзара орналасуы Екі түзу кеңістікте беттесуі, қиылысуы, айқасуы немесе
параллель
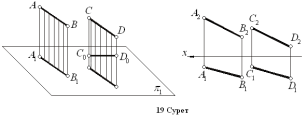
болуы мүмкін. Егер екі түзу кеңістікте өзара параллель болса, онда олардың аттас проекциялары да параллель болады (19 Сурет). Кері айтқан міндетті түрде дұрыс бола бермейді
(мысалы,
C0D0
мен AB түзулерін салыстырыңыздар). Қиылысқан түзулер -өзара ортақ бір нүктесі бар
түзулер (20 Сурет). Мысалы, AB және CD
түзулері
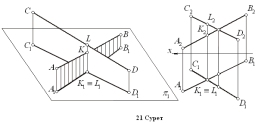
K нүктесінде қиылысады.Айқас түзулер – өзара ортақ нүктелері жоқ түзулер (21 Сурет) олар не қиылыспайды, не параллель емес.
Суретте K нүктесі AB түзуінің бойында, ал L нүктесі – CD түзуінің бойында жатыр. Олар π2 жазықтығынан бірдей қашықтықта жатыр (K1≡L1), бірақ π1 жазықтығынан қашықтықтары бірдей емес, L нүктесі K нүктесінен биік жатыр (L2 мен K2- ні салыстырыңыздар). Проекция жпазықтығын алмастыру:Бұл тәсіл бойынша, кеңістікте берілген денені өзгертпей қалдырады да, проекциялар жазықтықтарының кез – келгенін бізге қолайлы болып табылатын басқа жазықтықтармен алмастырып, дененің проекцияларын қайта тұрғызады. Жаңадан алған проекциялар жазықтығы ескі (алмастырылған) проекциялар жазықтығына перпендикуляр болып тұрғызылады (43 Сурет).
Суретте π1 жазықтығы π1 жазықтығына алмастырылған, π4﬩ π1.Π4- жаңа проекциялар жазықтығы.Π2-алмастырылған (ескі) проекциялар жазықтығы.π1-алмастырылмайтын проекциялар жазықтығы.А4АХ14=АА1=А2АХ Қорытындылар: а) Нүктенің жаңа проекциялары (А4)ж/е ескі алмастырылмайтын проекциясы (А1)жаңа проекция осіне (Х14) перпендикуляр бір түзудің бойында жатыр.А4А1=Х14; ә) нүктенің жаңа проекцияыынан (А4)жаңа осіне (Х14) дейінгі қашықтық, сол нүктенің ескі алмастыратын проекциясынан (А2) ескі осіне (Х12) дейінгі қашықтыққа тең: А4АХ14=А2АХ12
10.Проекцияларды түрлендіру тәсілдері Көп жағдайларда геометриялық есептерді шығару үшін проекцияларды түрлендіріп, денелерді бізге ыңғайландырып дербес жағдайға келтіру керек болады.Бұл есептерді шығарудың екі жолы бар:а) проекция жазықтықтарын алмастыру тәсілі;
б)
бұру тәсілі.Жазыќтықтаѓы
түзу:а)
егер түзу мен жазыќтыќтыњ екі ортаќ
нүктесі болса, онда түзу жазыќтыќта
жатады.ә) егер түзу жазыќтыќта бір
нүкте арќылы өтіп жєне осы жазыќтыќта
жатќан немесе осы жазыќтыќќа параллель
кез келген бір түзуге параллель болса,
онда бұл түзу осы жазыќтыќта жатады.Мысалы
(1.28 – сурет ): Б. (mn), L2 Т. к. L1, {L2 (mn ) ЕША 1)L2 m2 = 12 2) L2 n2 = 22 ; 3) ↕ 11 ^ 2 1 4) 1121= L1 1.28 – сурет
Жазықтықтың
ерекше түзулері:
Жазықтықтың ерекше түзулері деп,
осы жазықтықтың бойында жататын және
проекциялар жазықтарының біріне
параллель түзулерді атайды. 1.29- суретте
жазықтың екі ерекше түзуі – горизонталь
мен фронталь көрсетілген.а) жазықтықтың
горизонталі h1; h (ABC)
ә) жазықтың фронталі f2
1.29 – сурет Түзу мен жазықтықтың параллельдігі:Егер жазықтықтан тысқары алынған түзу осы жазықтықта жатқан түзулердің біріне параллель болса, онда ол түзу жазықтыққа параллель болады (1.30- сурет).
Б.
(mn),
L2
, А;{L
(m
n)} Т. к. L1
ЕША;
1) t2 L2 ,t ; 2)↕ t1 3) L1A1^ L1 t1 1.30 – сурет Өзара параллель жазықтықтар ;
Егер
бір жазықтықтың өзара қиылысқан екі
түзуі екінші жазықтықтың өзара
қиылысқан екі түзуіне параллель болса,
онда мұндай жазықтықтар өзара параллель
(1.31 - сурет). Б. (ABC), D Т. к. (mn), {( mn), (mn) (ABC) ; ЕША 1)mBCm2 B2C2, m1B1C12) nACn2 A2C2, n1A1C13)(mn ) (ABC) – параллель 1.31 – сурет проекциялаудың қасиеті бойынша
17.1Көпжақ деп барлық жағынан жазық көпбұрыштармен шектелген геометриялық денені атайды. Көпжақты шектейтін жазық көпбұрыштар оның жақтары болса, жақтардың өзара қиылысу сызықтары - оның қабырғалары (қырлары) болып табылады. Қабырғалардың ұштары - көпжақтың төбелері деп аталады. Көпжақты көп қырлы беттен құралған дене деп қарауға болады. Инженерлік тәжірибеде жиі тараған көпжақтар болып пирамидалар мен призмалар келеді.Пирамида деп негізі (табаны) қандай да бір көпбұрыш болып келетін, ал басқа жақтары S төбесі ортақ үшбұрыш болып табылатын көпжақты санайды (1-сурет). Пирамидаларды тік және тік емес деп екі топқа бөлуге болады. Тік пирамиданың төбесінен табанына түсірілген перпендикуляр табанның орталығына түседі. Дұрыс пирамида деп табаны дұрыс көпбұрыш болып табылатын тік пирамиданы атайды.
Призма
деп екі жағы (табандары) тең және өзара
параллель жазықтықтарда орналасқан
көпбұрыштар болып, ал қалған жақтары
параллелограммдардан тұратын көпжақты
атайды (2-сурет). Егер копжақтың табанында
параллелограммдар жатса, онда призманы
параллелепипед деп атайды. Призмаларды
тік және көлбеу призмалар деп екі
топқа бөледі. Тік призманың жақтары
тік төртбұрыштар болады және табандарымен
90º
бұрышты жасайды. Табаны дұрыс n бұрыш
болатын тік призманы дұрыс n бұрышты
призма дейді.Ортогональдық сызбада
кез келген көпжақ оның төбелері
(нүктелер), қабырғалары (түзу кесінділері)
және жақтары (жазық фигуралар) арқылы
берілуі мүмкін. 3-суретте көпжақтың
ортогональдік сызбада берілуінің
үлгісі көрсетілген.Көпжақтың төбелері
А,
В, С
және S
нүкте-лерімен берілген, қабырға-лары
АВ,
ВС, СА, АS,
ВS,
СS
кесінділерімен, ал жақтары АВС,
АВS, ВСS
және САS
үшбұрышта-рымен берілген.Ортогональдік
сызба-да көпжақтың жақтары мен
қабырғаларының көріне-тіндігі келесі
ережелердің көмегімен анықталады.1)
Көпжақ проекци-ясының сыртқы контурын
құрайтын қабырғаларының проекциялары
әрқашан да көрінеді. Сондықтан фронталь
проекциялау жазықтықтағы көпжақтың
А2В2,
В2С2,
С2S2,А2S2
проекциялары,ал
горизонталь
проекциялау жазықтықтағы А1В1,
В1S1,
S1С1,
С1А1
проекцялары көрінеді. 2) Көпжақтың
басқа қабырғалары бәсекелес нүктелер
арқылы анықталады. 3-суретте АS
қабырғасы ВС
қабырғасынан жоғары орналасқандықтан
А1S1қабырғасының
горизонталь жазықтығындағы проекциясы
көрінеді (3 нүктесі 4 нүктесінен жоғары
z3>
z4).
Фронталь жазықтығындағы проекцияларды
қарастырсақ, келесіні байқаймыз:АС
түзуі ВS
түзуіне қарағанда бақылаушыға жақын
жатады (1 нүктесі 2 нүктесінен жақын
y1>
y2),
сондықтан В2S2
проекциясы көрінбейді, ал А2С2
проекциясы көрінеді.3) Егер көпжақтың
бір жағының барлық қабырғалары
көрінетін болса, онда сол жақ толық
көрінетіні мәлім. Суретке қарағанда
фронталь проекциялау жазықтықтағыАВC,
ASC
және горизонталь проекциялау
жазықтықтағы
АВS, AСS
жақтарының проекциялары көрінеді.4)
Егер көпжақтың жағын құраған кем
дегенде бір қабырғасы көрінбейтін
болса, онда сол жақ көрінбейді. 3-суретте
фронталь проекциялау жазықтықтағы
АВS, BCS
және горизонталь проекциялау
жазықтықтағы
АВC, BСS
жақтарының проекциялары көрінбейді.Беттің
жазықтықпен қимасы деп, нүктелері
қиылушы бетпен және қиюшы жазықтыққа
ортақ болып түсетін жазық фигураны
айтамыз.
17.2Қиюшы
жазықтық деп қиманы жасайтын жазықтықты
атаймыз. Көп жақты немесе қисық
беттердің қиюшы жазықтықпен қиылысуынан
пайда болған фигураны қима немесе
қиманың фигурасы деп атаймыз. Кез келген көпжақтың жазықтықпен қиылысуынан алынатын жазық фигура көпбұрыш болады және оның қабырғаларының саны көпжақтың жазықтық қиятын жақтар санына сәйкес келеді. Көпжақтың қабырғаларының қиюшы жазықтықпен қиылысу нүктелері көпбұрыштың төбелері болып келсе, қиюшы жазықтық пен жақтардың қиылысуындағы түзу сызықтар бүйірі болып табылады. Егерде қиюшы жазықтық проекциялаушы болса, көпжақтың жазықтықпен қиылысу сызығын тұрғызу едәуір оңай болады. Осындай жағдайда қиылысу сызығының комплексті сызбадағы проекциясы алдын ала анықталып тұрады, себебі, ол проекция проекциялаушы жазықтықтың проекциясымен сәйкес келеді.
18.Көпжақтар
жайлы негізгі түсініктер.Көпжақ
деп барлық жағынан жазық көпбұрыштармен
шектелген геометриялық денені атайды.
Көпжақты шектейтін жазық көпбұрыштар
оның жақтары болса, жақтардың өзара
қиылысу сызықтары - оның қабырғалары
(қырлары) болып табылады. Қабырғалардың
ұштары - көпжақтың төбелері деп аталады.
Көпжақты көп қырлы беттен құралған
дене деп қарауға болады. Инженерлік
тәжірибеде жиі тараған көпжақтар
болып пирамидалар мен призмалар
келеді.Пирамида деп негізі (табаны)
қандай да бір көпбұрыш болып келетін,
ал басқа жақтары S төбесі ортақ үшбұрыш
болып табылатын көпжақты санайды
(1-сурет). Пирамидаларды тік және тік
емес деп екі топқа бөлуге болады. Тік
пирамиданың төбесінен табанына
түсірілген перпендикуляр табанның
орталығына түседі. Дұрыс пирамида деп
табаны дұрыс көпбұрыш болып табылатын
тік пирамиданы атайды. Призма деп екі
жағы (табандары) тең және өзара параллель
жазықтықтарда орналасқан көпбұрыштар
болып, ал қалған жақтары параллелограммдардан
тұратын көпжақты атайды (2-сурет). Егер
копжақтың табанында параллелограммдар
жатса, онда призманы параллелепипед
деп атайды. Призмаларды тік және көлбеу
призмалар деп екі топқа бөледі. Тік
призманың жақтары тік төртбұрыштар
болады және табандарымен 90º
бұрышты жасайды. Табаны дұрыс n бұрыш
болатын тік призманы дұрыс n бұрышты
призма дейді.
|

 1.1
1.1
 1.2
мундагы
1.2
мундагы 1.3
1.3 1.4
1.4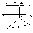


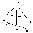 1.21-1.22-сурет.
1.21-1.22-сурет.
 1.37-сурет
1.37-сурет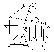


 тер.
Жазылатын беттер үшеу: торс, конустық
және цилиндрлік беттер.Цилиндрлік
бет:
Цилиндрлік бет түзу жасаушы L-дың қисық
бағыттаушы m- ның бойымен қозғалғанда
пайда болады. Бұл жерде жасаушы Алдан
ала берілген бір бағыт S- ке әр уақытта
параллель болуы керек (1.41- сурет).
тер.
Жазылатын беттер үшеу: торс, конустық
және цилиндрлік беттер.Цилиндрлік
бет:
Цилиндрлік бет түзу жасаушы L-дың қисық
бағыттаушы m- ның бойымен қозғалғанда
пайда болады. Бұл жерде жасаушы Алдан
ала берілген бір бағыт S- ке әр уақытта
параллель болуы керек (1.41- сурет). 1.40-с
1.40-с 1.41-с
1.41-с 1.42-с
1.42-с
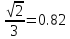 - ге тең болады,
- ге тең болады,
 изометрия
изометрия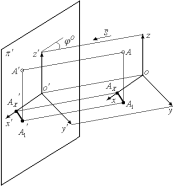

 ,
n=
,
n= Осьтер
арасындағы бұрыш 4 Суретте көрсетілген.
Осьтер
арасындағы бұрыш 4 Суретте көрсетілген.

 1.6
1.6
 1.7
Суретте:1-горизонталь
проек/лар жазықтығы; 2-фронталь
проект/лар жаз/ғы.А1–Анүктесінің
горизонталь проект/сы;А2-А
нүк/нің фронталь проекциясы,Х-проек/лар
осі;Ах
–А нүктесінің х осіндегі проекциясы
боладыЕгер 1
жазыктыгын Х осiнен 900-ка
бурсак, 1
мен 2
жазыктыктары бiр жазыктыктын бойымен
беттеседi(1.7сурет).Осындай чертеж Монж
эпюрi
д.а.Монж
эпюрiнiн касиеттерi. 1.
Нуктенiн горизонталь проекциялары
аркашан да оське перпендикуляр бiр
вертикаль сызыктын бойында жатады.Ол
сызык (А2А1)байланыс
сызыгы д.а.2. Нуктеден 1-ге
дейiнгi каштык А2Ах=АА1
кесiндiсiне
тен,ол нукненiн биiктiгi д.а.Ал 2-ге
дейiнгi каштык А2А1=Ах
А1,ол
нуктенiн терендiгi .Проекция жазыктыетарынын
иылысу сызыктары проекция осьтерi
д.а. Х-абцисса,У-ордината,Z-апликата.
Осьтердин тогысу нуктеси-координатлар
басы
д.а.Нуктенин кенситикте орналаскан
жерин координаталармен беруге
болады.А(ХА,УА,ZА)
немесе А(4,3,5).
1.7
Суретте:1-горизонталь
проек/лар жазықтығы; 2-фронталь
проект/лар жаз/ғы.А1–Анүктесінің
горизонталь проект/сы;А2-А
нүк/нің фронталь проекциясы,Х-проек/лар
осі;Ах
–А нүктесінің х осіндегі проекциясы
боладыЕгер 1
жазыктыгын Х осiнен 900-ка
бурсак, 1
мен 2
жазыктыктары бiр жазыктыктын бойымен
беттеседi(1.7сурет).Осындай чертеж Монж
эпюрi
д.а.Монж
эпюрiнiн касиеттерi. 1.
Нуктенiн горизонталь проекциялары
аркашан да оське перпендикуляр бiр
вертикаль сызыктын бойында жатады.Ол
сызык (А2А1)байланыс
сызыгы д.а.2. Нуктеден 1-ге
дейiнгi каштык А2Ах=АА1
кесiндiсiне
тен,ол нукненiн биiктiгi д.а.Ал 2-ге
дейiнгi каштык А2А1=Ах
А1,ол
нуктенiн терендiгi .Проекция жазыктыетарынын
иылысу сызыктары проекция осьтерi
д.а. Х-абцисса,У-ордината,Z-апликата.
Осьтердин тогысу нуктеси-координатлар
басы
д.а.Нуктенин кенситикте орналаскан
жерин координаталармен беруге
болады.А(ХА,УА,ZА)
немесе А(4,3,5). 1.9
1.9 1.10
1.10



 1.45
а)
1.45
а) 1.45
ә)
1.45
ә) 1.46
1.46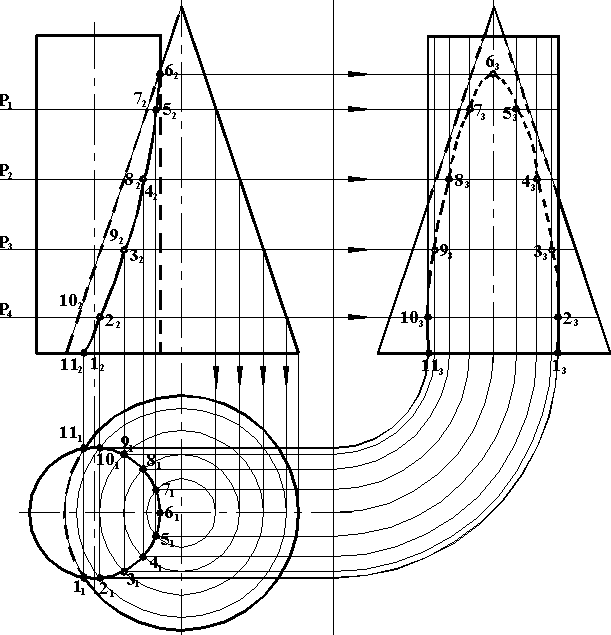 және цилиндрлік айналу беттері, сфера
, тор, айналу эллипсоиды, айналу
параболоиды, т. с. с.
және цилиндрлік айналу беттері, сфера
, тор, айналу эллипсоиды, айналу
параболоиды, т. с. с. 1)
һ α
(АВС)] 2) π 4
һ → Х14һ1
3)D4,
A4,
B4,C4
4)D4K4A4B4
5)D4K4
= [ D ∙ α].
1)
һ α
(АВС)] 2) π 4
һ → Х14һ1
3)D4,
A4,
B4,C4
4)D4K4A4B4
5)D4K4
= [ D ∙ α].
 1)h
2)4
h x14
h1
1)h
2)4
h x14
h1