5. Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.

   Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.

 

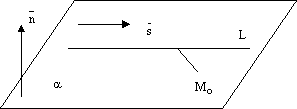
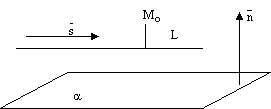
                                           рис.6. рис.7.

           

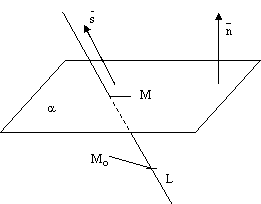
                                          рис.8.

Теорема. Пусть плоскость  задана общим уравнением  , а прямая L задана каноническими уравнениями 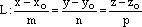или параметрическими уравнениями 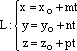,   , в которых  – координаты нормального вектора плоскости ,  – координаты произвольной фиксированной точки прямой L,   – координаты направляющего вектора прямой L. Тогда:

1) если , то прямая L пересекает плоскость  в точке, координаты которой  можно найти из системы уравнений

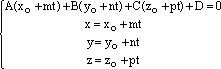             ;           (7)

2) если  и , то прямая лежит на плоскости;

3) если  и , то прямая параллельна плоскости.

   Доказательство. Условие  говорит о том, что векторы  и  не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.

   Если , то это означает, что . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка . Если , то точка  – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.

   Если , а , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.

Теорема доказана.

Определение 1. Угол между прямой лежащей в одной плоскости с другой плоскостью есть угол между этой прямой и её проекцией на эту плоскость. Теорема 1. Синус угла между прямой лежащей в одной плоскости с другой плоскостью равен произведению синуса угла между этими плоскостями на синус угла между прямой и ребром двугранного угла, о6разованного этими плоскостями.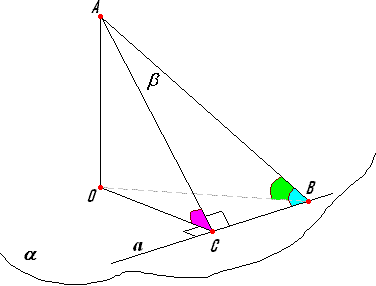

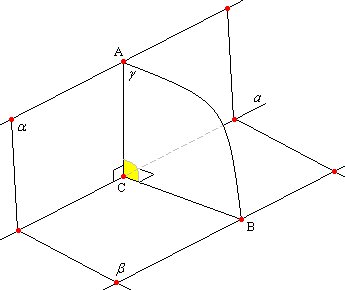
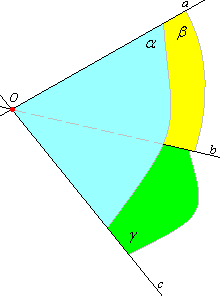
Доказательство. Пусть даны плоскости  и  и прямая их пересечения с. А – точка, лежащая в плоскости  (и не лежащая в плоскости ). Точка О – основание перпендикуляра, опущенного из точки А на плоскость , В – произвольная точка на прямой с. Из точки А опустим перпендикуляр на прямую с получим точку С. Соединим точки С и О. СО перпендикулярна прямой с по теореме о трех перпендикулярах (АС – наклонная, перпендикулярная прямой в плоскости с). 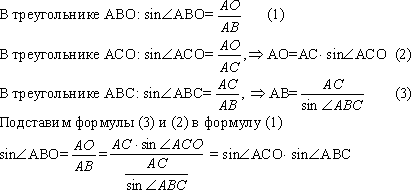Это тождество также называют формулой связи синусов. Обычно говорят просто - связь синусов (используя связь синусов, получаем...).

5. Взаимное расположение плоскостей в пространстве. Угол между плоскостями. Двугранный угол. Измерение двугранных углов.

Пусть уравнения A₁x + B₁y + C₁z + D₁ = 0, A₁² + B₁² + C₁² ≠ 0 и A₂x + B₂y + C₂ z + D₂ = 0,

A₂² + B₂² + C₂² ≠ 0, описывают в одной и той же декартовой системе координат две плоскости, нормальные векторы которых соответственно N₁ = (A₁, B₁, C₁) и N₂ = (A₂, B₂, C₂). Угол между этими плоскостями — это угол между их нормальными векторами и определяется по формуле

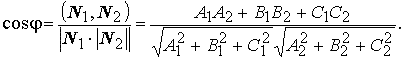
Плоскости совпадают, тогда и только тогда, когда существует отличное от нуля число k такое, что одновременно выполнены равенства A₁= kA₂ ,B₁= kB₂ , C₁= kC₂ , D₁= kD₂.

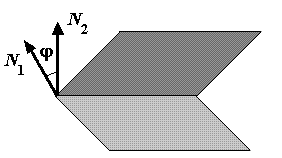
Плоскости параллельны, тогда и только тогда, когда существует отличное от нуля число k такое, что одновременно выполнены равенства A₁= kA₂ ,B₁= kB₂ , C₁= kC₂ и D₁≠ kD₂ (нормальные векторы плоскостей параллельны).

Плоскости перпендикулярны, тогда и только тогда, когда A₁A₂ + B₁B₂+ C₁C₂ = 0 (нормальные векторы плоскостей перпендикулярны).

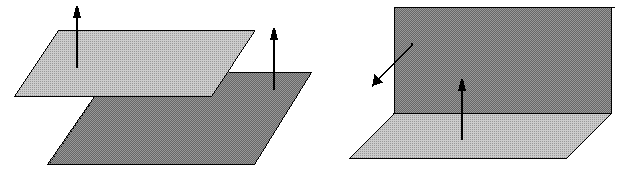
Угол между плоскостями. 

  Угол между двумя плоскостями в пространстве  связан с углом между нормалями к этим плоскостям ₁ соотношением:  = ₁ или  = 180⁰ - ₁, т.е.

cos = cos₁.

  Определим угол ₁. Известно, что плоскости могут быть заданы соотношениями: 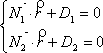, где(A₁, B₁, C₁),

(A₂, B₂, C₂). Угол между векторами нормали найдем из их скалярного произведения: .   Таким образом, угол между плоскостями находится по формуле: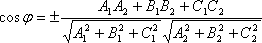  

Определение 1. Двугранным углом называется часть пространства, ограниченная двумя полуплоскостями, границей каждой из которых служит их общая прямая. Двугранный угол также называют углом между данными плоскостями.

Определение 2. Плоскости (полуплоскости), которые ограничивают двугранный угол, называются гранями двугранного угла.

Определение 3. Линия пересечения граней двугранного угла называется ребром двугранного угла. Определение 4. Линейным углом двугранного угла называется угол, образованный двумя полупрямыми, полученными при пересечении граней двугранного угла плоскостью, перпендикулярной ребру этого двугранного угла. Значение линейного угла данного двугранного угла есть значение данного двугранного угла.