2. Предел функции, его свойства и геометрический смысл. Предел функции и бмф. Примеры

Пусть функция у=ƒ (х) определена в некоторой окрестности точки х_о, кроме, быть может, самой точки х_о.

Сформулируем два, эквивалентных между собой, определения предела функции в точке.

Определение 1 (на «языке последовательностей», или по Гейне).

Число А называется пределом функции у=ƒ(х) в точке x₀ (или при х х_о), если для любой последовательности допустимых значений аргумента x_n, n є N (x_nx₀), сходящейся к х_о последовательность соответствующих значений функции ƒ(х_n), n є N, сходится к числу А

В этом случае пишут        или ƒ(х)—>А при х→х_о. Геометрический смысл предела функции:  означает, что для всех точек х, достаточно близких к точке х_о, соответствующие значения функции как угодно мало отличаются от числа А.

Определение 2 (на «языке ε», или по Коши).

Число А называется пределом функции в точке х_о (или при х→х_о), если для любого положительного ε найдется такое положительное число δ, что для все хх_о, удовлетворяющих неравенству |х-х_о|<δ, выполняется неравенство |ƒ(х)-А|<ε.

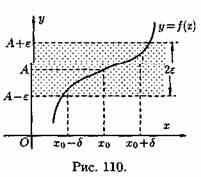
Геометрический смысл предела функции:

если для любой ε-окрестности точки А найдется такая δ-окрестность точки х_о, что для всех ххо из етой  δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис.) Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).

Функция f(x) называется бесконечно малой при ха, где а может быть числом или одной из величин , + или -, если.

Примеры: 1) Функция f(x) = tgx – бесконечно малая при x→0.

2) f(x) = ln (1+x) – бесконечно малая при x→0.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

3. Необходимый признак существования предела – ограниченность функции. Односторонние пределы функции в точке, их связь с пределом. Примеры.

Ограниченность функции.

Функция f(x) называется ограниченной на данном промежутке (a,b), если существуют некоторые числа m и M такие, что

m ≤ f(x) ≤ M, при хє(a,b).

Число m_o= inf {f(x)} [x є (a,b)] = max m называется нижней гранью функции ,

а число M_o= sup {f(x)} [x є (a,b)]=min M называется верхней гранью функции на данном промежутке (a,b).

Разность M_o- m_o называется колебанием функции на промежутке (a,b).

Односторонние пределы.

Число A' называется пределом слева функции f(x) в точке a:

если |A' - f(x)| < ε при 0 < a - x < δ (ε).

Аналогично, число A" называется пределом справа функции f(x) в точке a:

если |A" - f(x) |< ε при 0 < x - a < δ (ε).

Для  существования предела функции в точке необходимо и достаточно, чтобы f (a - 0) = f(a + 0).